06 - Resistenze al moto veicoli terrestri - VIT
06 - Resistenze al moto veicoli terrestri - VIT
[[6. Resistenze al moto veicoli terrestri - VIT.pdf]]
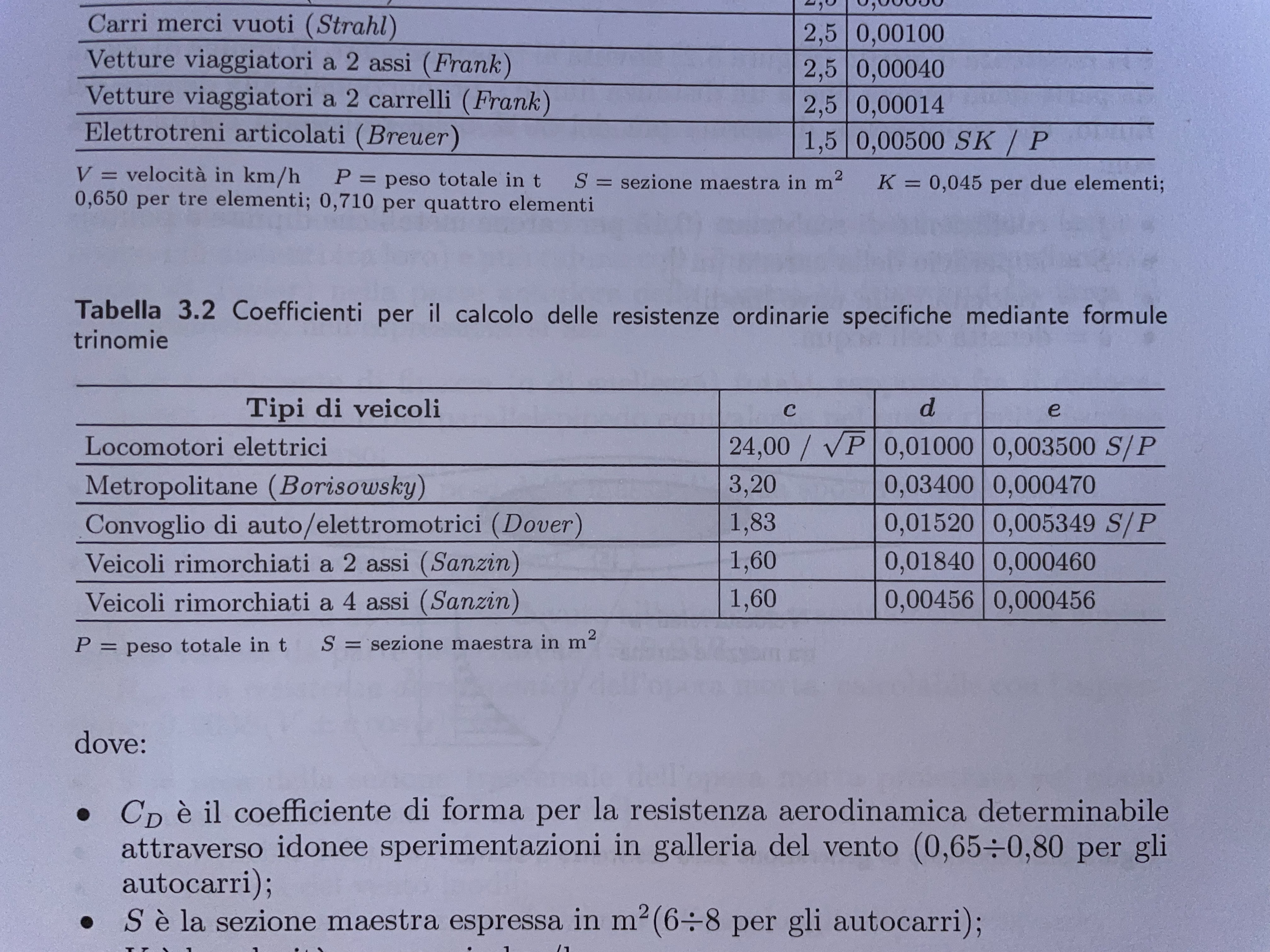
- Resistenze al moto ordinarie - in qualunque condizione di moto
- Rotolamento nella coppia cinematica ruota-rotaia
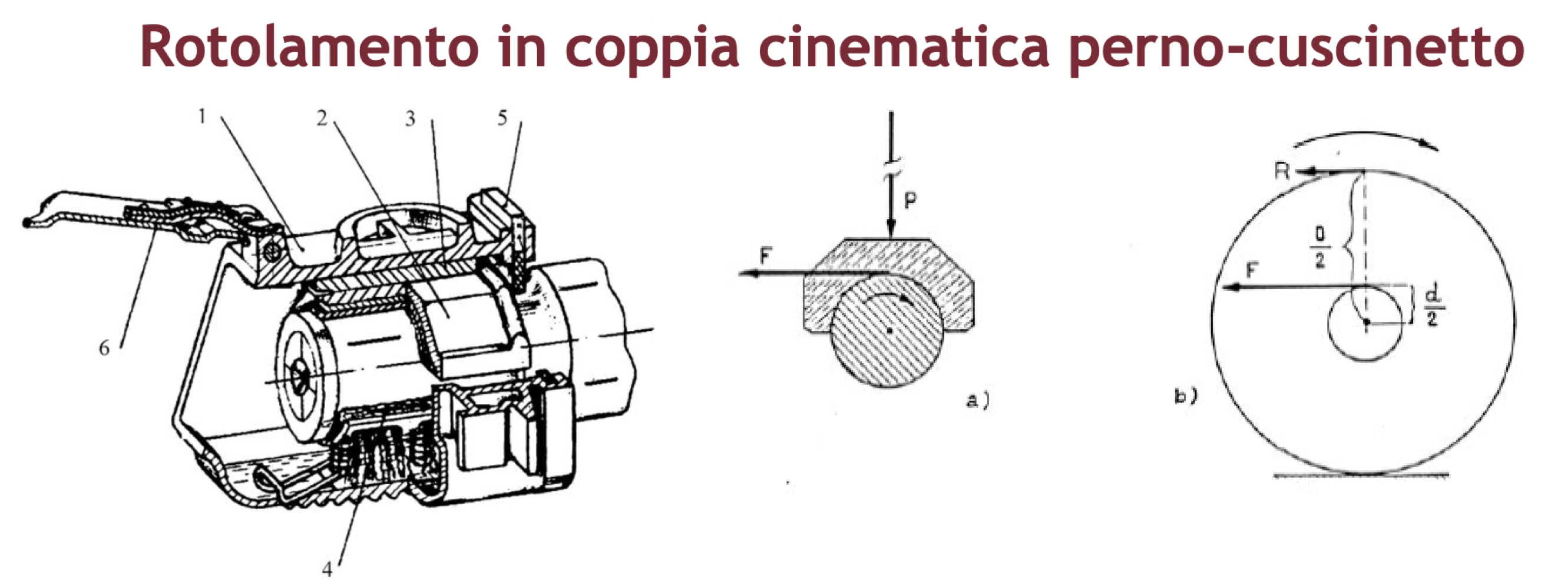
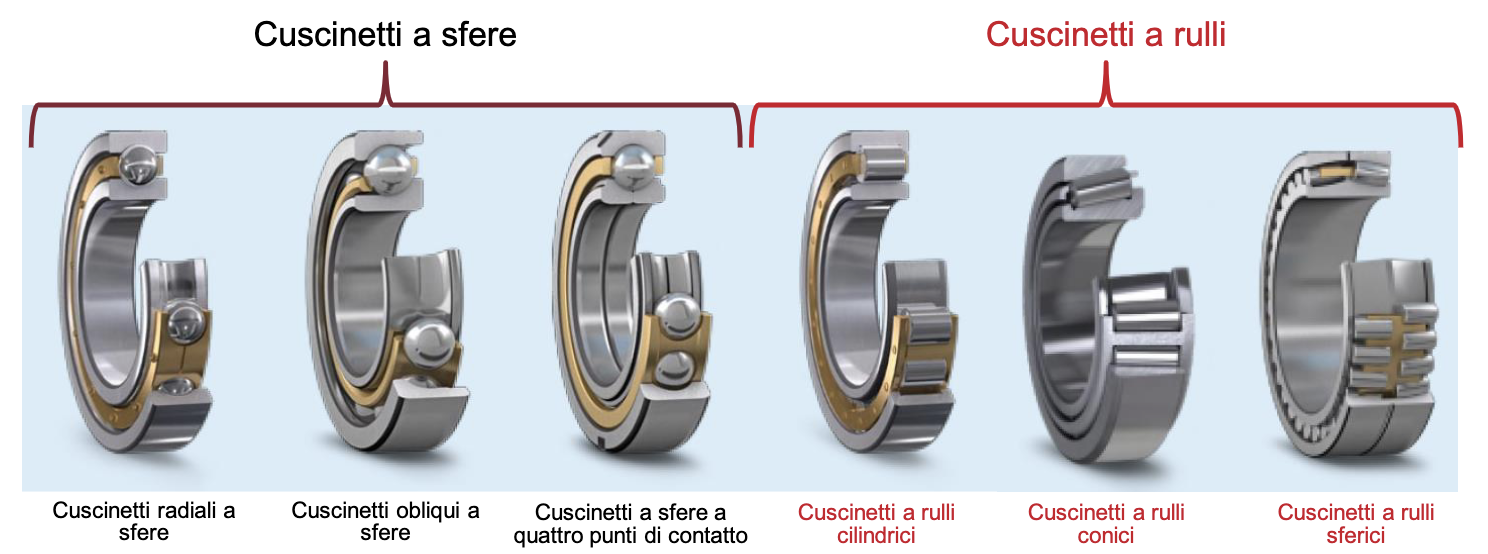
- Rotolamento nella coppia cinematica perno-cuscinetto
- Aerodinamica
- Resistenze al moto addizionali
- Inerzia
- Livelletta
- Curva
- Parallelismo imposto dal passo rigido fra due assi
- Forza di bordino
- Aerodinamica in galleria
Le resistenze al moto possono o meno comportare dissipazione di energia.
L'inerzia non comporta dissipazione di energia. Se facciamo accumulare una certa velocità al veicolo questo la può sfruttare in deriva.
Anche la livelletta: il lavoro compiuto per far salire il veicolo è conservata fino alla discesa in forma di energia potenziale.
Resistenze addizionali
Le resistenze addizionali sono quelle:
- In #Curva
- #Aerodinamica in galleria
- #Inerzia
- #Livelletta
Inerzia
Ogni variazione dello stato di moto fa nascere una forza che si oppone a tale variazione: la forza di inerzia.
È richiesta una quantità di energia extra ad esempio per accelerare la massa del veicolo, nonché tutte le masse rotanti
Livelletta
In presenza di una pendenza da superare, oltre all'energia necessaria a spostare il veicolo sull'asse orizzontale, sarà necessario fornire un'energia al fine di vincere la forza di gravità.
Curva
- Parallelismo rigido tra assili
- Lavoro dissipativo per l'attrito del contatto ruota-rotaia
- Diversa percorrenza di ruote dello stesso asse
- Compensata da ruota troncoconica
- Urti tra bordino e rotaia esterna
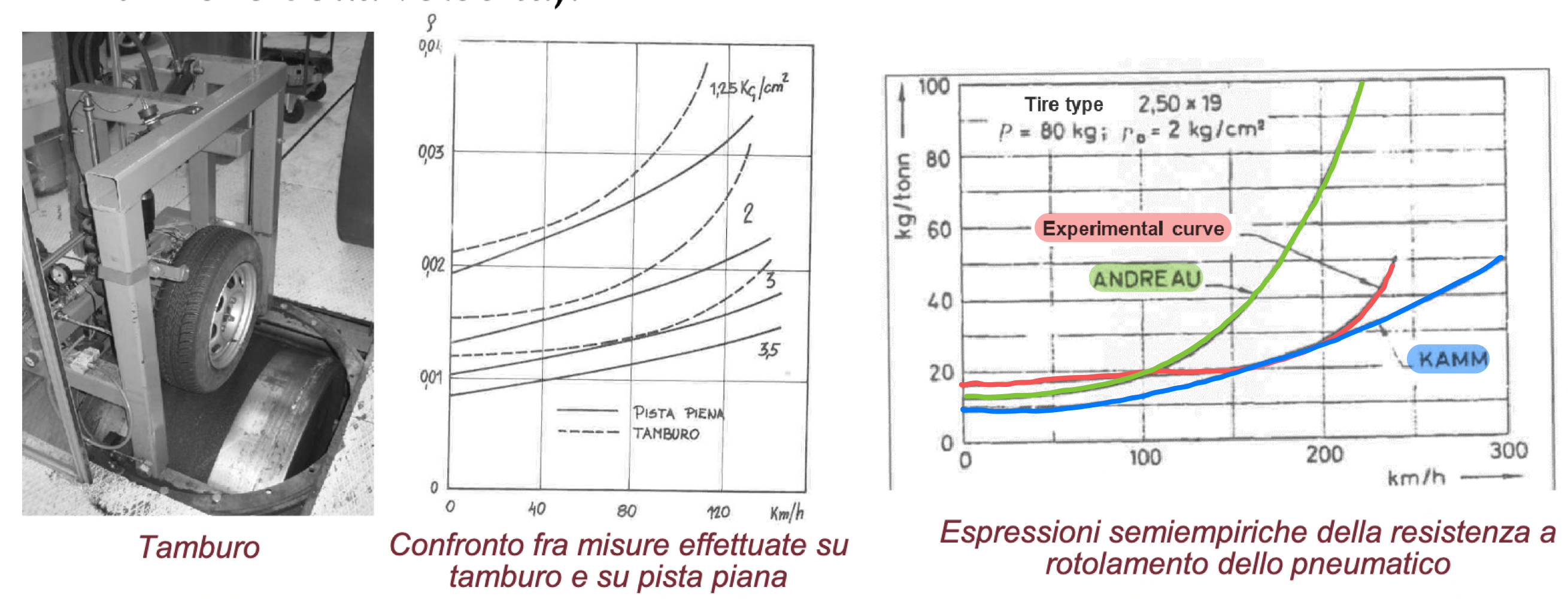
Aerodinamica in galleria
Si sfruttano formule sperimentali.
La resistenza aerodinamica in galleria è dovuta a:
- Sovrappressione anteriore e depressione posteriore
- Dipende dalla posizione del treno nella galleria
Determinazione sperimentale delle resistenze
Metodo del lanciamento
Si porta il veicolo a una velocità
Ogni
Metodo della vettura dinamometrica
Un altro metodo di misura delle resistenze al moto è la vettura dinamometrica.
Si posiziona un'apposita vettura, detta vettura dinamometrica fra la locomotiva e la colonna rimorchiata in esame.
A bordo della vettura rimorchiata trovano posto:
- Dinamometro
- Odografo - misura spazi percorsi
- Cronometro - misura i tempi
- Tachimetro - Determina velocità
- Wattmetro - Determina potenza scambiata
- Integratore del lavoro - Determina energia fornita
Se la vettura dinamometrica è dello stesso tipo di quelle della colonna rimorchiata, la misurazione si può effettuare sulla parte anteriore della VD, altrimenti bisogna usare necessariamente la parte posteriore.
Si percorre un tratto
la resistenza sarà
dove
Se la locomotiva è elettrica conosco già la potenza assorbita dal pantografo,