04 - Dinamica dei veicoli - VIT

Marcia in curva

Quando un treno percorre una curva, si genera una forza, detta forza centrifuga esprimibile come:

F_{c} = m a_{c} = m \frac{v^{2}}{R}

dove

$v =$ Velocità del veicolo
$R =$ Raggio della curva
$a_{c} =$ Accelerazione centripeta

La forza centrifuga ha le seguenti caratteristiche:

Agisce sulla rotaia esterna
È diretta verso l'esterno della curva
Tende a ribaltare il veicolo verso l'esterno
Riduce il comfort dei passeggeri

Stabilità a sbandamento e ribaltamento

Stabilità allo sbandamento - senza sovralzo

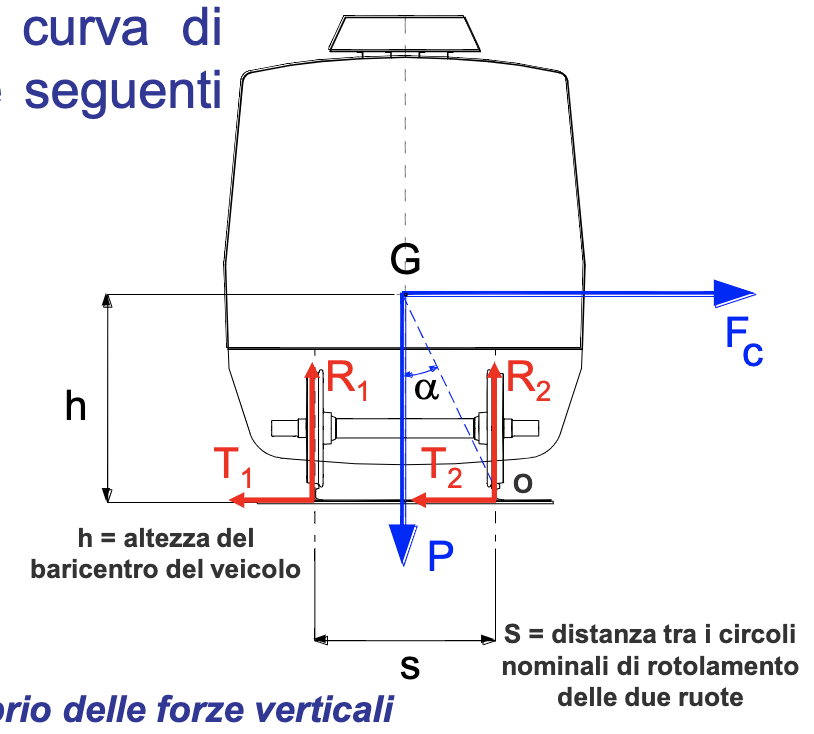
Dato un veicolo che percorre una curva di raggio $R$ a velocità $V$ , su di questo agiscono le seguenti forze:

$P = m g$ - Forza peso
$F_{c} = \frac{P}{g} \frac{v^{2}}{R}$ - Forza centrifuga
$R_{1}, R_{2}$ - Reazioni verticali
$T_{1}, T_{2}$ - Reazioni trasversali

Affinché il veicolo percorra la curva a velocità costante, si possono scrivere le seguenti equazioni di equilibrio delle forze e dei momenti:

{\begin{cases} X : R_{1} + R_{2} - m g = 0 \\ Y : T_{1} + T_{2} - F_{c} = 0 \\ M_{O} : F_{c} h + R_{1} s - m g \frac{s}{2} = 0 \end{cases}

che diventa, esplicitando la forza centrifuga

{\begin{cases} X : R_{1} + R_{2} - m g = 0 \\ Y : T_{1} + T_{2} - m \frac{v^{2}}{R} = 0 \\ M_{O} : F_{c} h + R_{1} s - m g \frac{s}{2} = 0 \end{cases}

Ricordando inoltre le condizioni di aderenza, ipotizzando il coefficiente di aderenza uguale per tutte le ruote:

T_{1} \leq φ R_{1} T_{2} \leq φ R_{2}

L'equazione di equilibrio orizzontale può essere riscritta

T_{1} + T_{2} = m \frac{v^{2}}{R} \leq φ (R_{1} + R_{2})

Da cui si ottiene il limite imposto alla velocità dallo sbandamento:

limite allo sbandamento - senza sovralzo

$\frac{v^{2}}{R} \leq φ g$

dove si è usata l'equazione all'equilibrio verticale.
Si possono inoltre ricavare le reazioni alle due ruote:

{\begin{cases} R_{1} = P (\frac{1}{2} - \frac{v^{2} h}{R s g}) \\ R_{2} = P (\frac{1}{2} + \frac{v^{2} h}{R s g}) \end{cases}

da cui si evince che il carico aumenta all'esterno e diminuisce all'interno. Occorre quindi imporre un ulteriore limite, al fine di evitare il ribaltamento

Stabilità al ribaltamento - senza sovralzo

Poiché il vincolo di appoggio della ruota sulla via non è bidirezionale (reagisce solo a compressione) occorre imporre che la reazione vincolare non cambi segno rispetto a quello ipotizzato e cioè che sia non negativa:

R_{1} \geq 0

Ricordando il valore della reazione interna:

R_{1} = P (\frac{1}{2} - \frac{v^{2} h}{R s g})

vogliamo quindi

\frac{1}{2} \geq \frac{v^{2} h}{R s g}

Questo impone la condizione

\frac{v^{2}}{R} \leq \frac{s g}{2 h}

Si osservi che $\frac{s}{2 h}$ può essere riscritto come la tangente dell'angolo $α$ :

limite al ribaltamento - senza sovralzo

$\frac{v^{2}}{R} \leq g \tan α$

Stabilità allo sbandamento con sovralzo

limite allo sbandamento - con sovralzo

$\frac{v^{2}}{R} \leq g φ \frac{1 + \tan (\frac{γ}{φ})}{1 - φ \tan (γ)}$

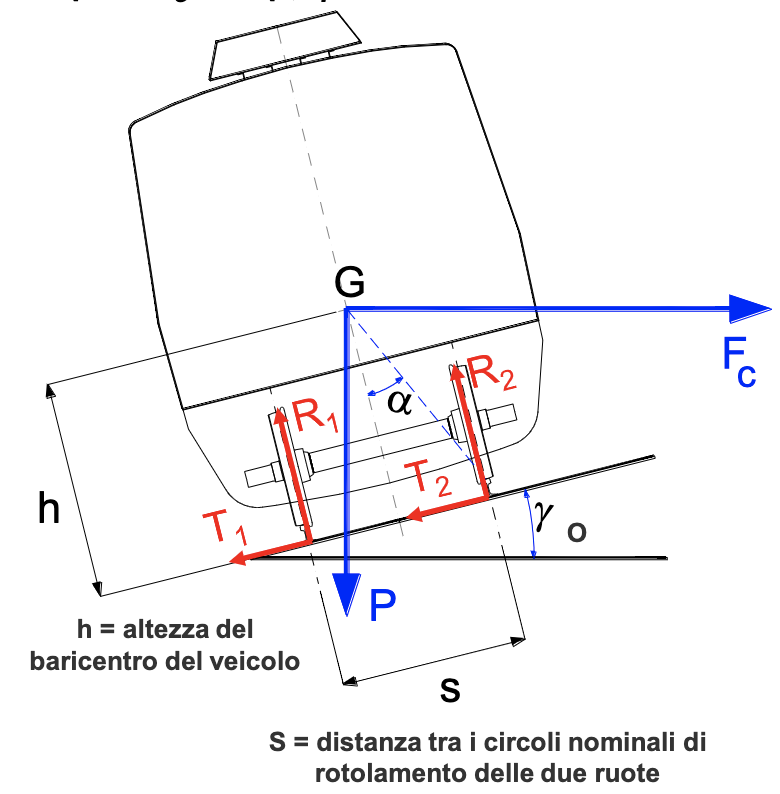
Stabilità al ribaltamento - con sovralzo

limite allo sbandamento - con sovralzo

$\frac{v^{2}}{R} \leq g \tan (α + γ)$

Sovralzo

sovralzo

Il sovralzo è una sopraelevazione della rotaia esterna rispetto a quella interna. In curva si realizza elevando la quota della rotaia esterna in modo che la forza peso possa compensare la forza centrifuga.

Il sovralzo ha delle limitazioni dovute a:

differenze di velocità tra i treni che percorrono la linea
Il fatto che un veicolo deve potersi fermare in curva senza ribaltarsi

In Italia, il valore massimo del sovralzo è di $160 m m$ .

Il sovralzo in realtà ha una duplice funzione. Oltre ad aumentare la velocità massima in curva, assicura un miglior comfort dei passeggeri. Vengono infatti limitate:

La componente dell'accelerazione centrifuga parallela al piano del ferro (accelerazione non compensata) $a_{n c}$
La componente dell'accelerazione centrifuga parallela al pavimento del veicolo (accelerazione laterale del passeggero) $a_{l p}$
Se si suppone che il pavimento del treno si mantenga parallelo al piano del ferro, si può dire che

a_{n c} = a_{l p}

Sotto questa ipotesi, i viaggiatori sono sottoposti a una forza laterale $F_{l p}$ pari alla forza non compensata $F_{n c}$ .

F_{l p} = F_{n c} = F_{c}^{'} - P^{'} = m \frac{v^{2}}{R} \cos α - m g \sin α

Dove si sono considerate solo le componenti orizzontali di ciascuna forza, essendo $α$ l'inclinazione del piano di binario. Considerando $\cos α \approx 1$ si ha che

a_{l p} = a_{n c} = \frac{v^{2}}{R} - g \sin α = \frac{v^{2}}{R} - g \frac{h}{s}

Fissato il valore massimo di accelerazione non compensata che può subire un passeggero, e fissato il sovralzo massimo sulla base dei limiti descritti prima, si può trovare la velocità massima in funzione del raggio della curva:

v = \sqrt{a_{n c} + g \frac{h}{s}} \cdot \sqrt{R}

Sulla base di queste considerazioni, in funzione dell'accelerazione max che il treno può subire, si definisce il #Rango del treno.

Rango

Treni ad assetto variabile

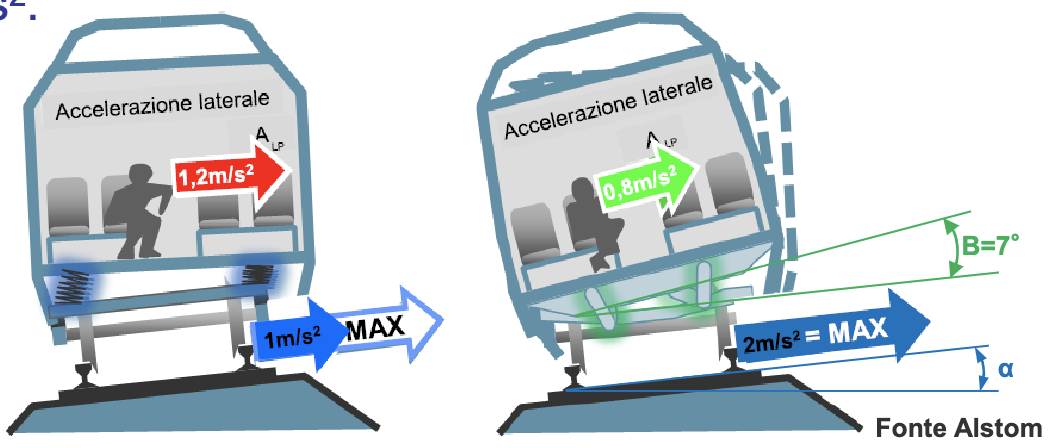
Alcuni treni possono modificare il proprio assetto in curva per diminuire l'accelerazione trasmessa ai passeggeri rispetto a quella non compensata dal treno.s
I treni ad assetto variabile permettono infatti l'inclinazione di un ulteriore angolo $β$ verso l'interno della curva del pavimento.

Stabilità allo svio

In ferrovia, più che alla stabilità allo sbandamento si è interessati alla stabilità allo svio.
Nella ruota ferroviaria infatti il bordino rappresenta un fine corsa nello spostamento laterale della sala montata.

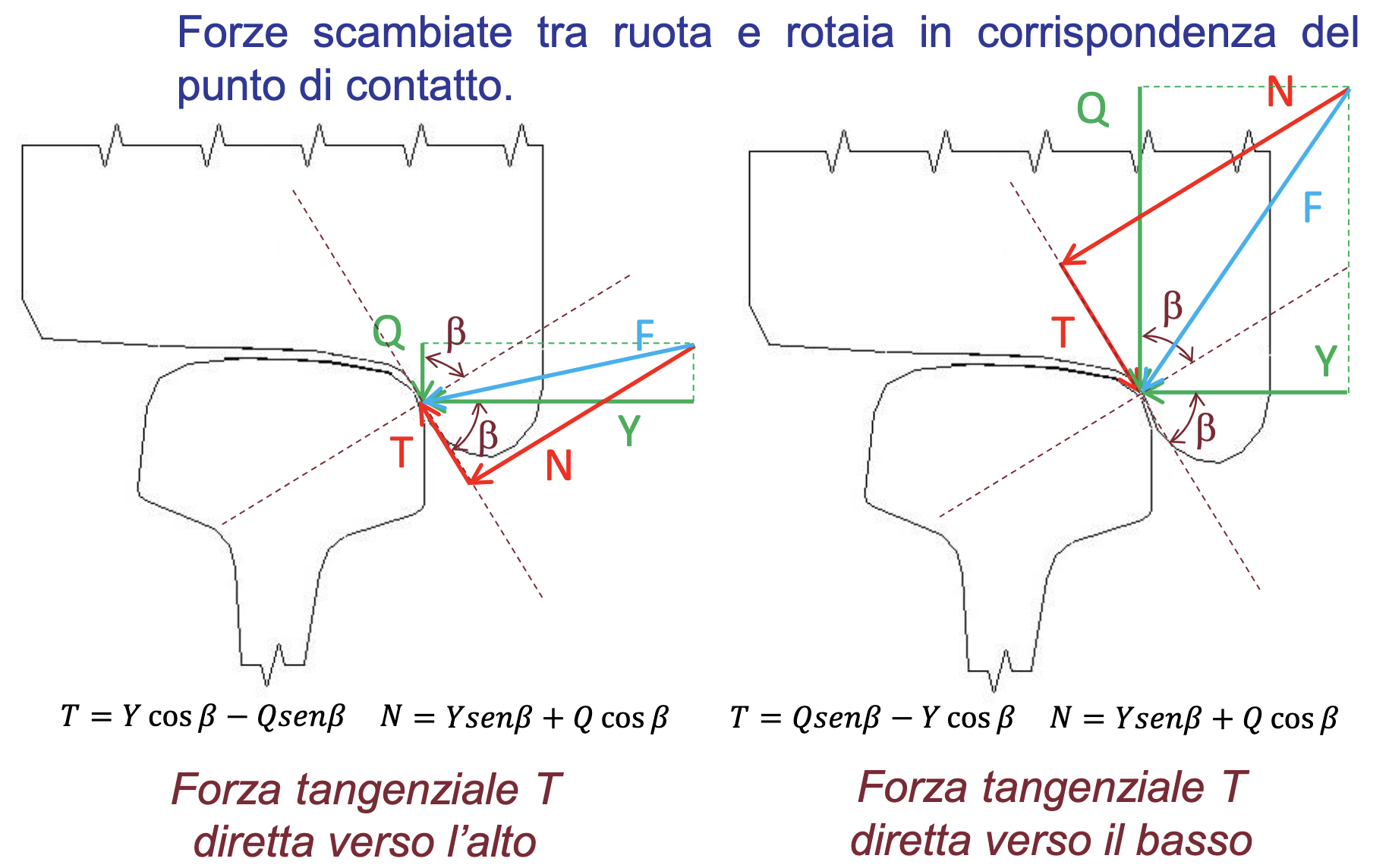
Si guardi al punto di contatto bordino-rotaia
La ruota trasmette alla rotaia due forze:

$Q =$ Peso gravante sulla ruota
$Y =$ Forza orizzontale dovuta alla forza centrifuga
La somma vettoriale di $Q$ e $Y$ fornisce la forza $F$ trasmessa dalla ruota alla rotaia.

Nel punto di applicazione, la forza $F$ può essere scomposta in due componenti, una tangenziale ( $T$ ) e una normale ( $N$ ) alla superficie di contatto:

\begin{array}{r} T = Y \cos β - Q \sin β \\ N = Y \sin β + Q \cos β \end{array}

essendo $β$ l'inclinazione della superficie di contatto rispetto all'orizzontale.

Una prima forma della condizione di stabilità allo svio prevede che la componente tangenziale non sia superiore alla forza di attrito che può nascere al contatto:

T \leq f N

che si esplicita:

Y \cos β - Q \sin β \leq f (Y \sin β + Q \cos β)

Questo nell'ipotesi in cui la forza tangenziale sia diretta verso l'alto (diagramma di SX).

Formula di Pochet-Nadal

La formula di Pochet-Nadal offre un criterio più prudenziale di stabilità

Supponendo di trovarci già nella condizione in cui il bordino sia già risalito rispetto alla rotaia, e che la forza tangenziale sia diretta verso il basso, impongo che la forza tangenziale sia maggiore dell'attrito

T \geq f N

ovvero, esplicitando

Y \cos β - Q \sin β \geq f (Y \sin β + Q \cos β)

la quale può essere espressa nella forma:

formula di pochet-nadal

$\frac{Y}{Q} \leq \frac{\tan β - f}{1 + f \tan β}$
dove $\frac{Y}{Q}$ è detto coefficiente di svio

L'usura del bordino aumenta $β$ , migliorando la stabilità allo svio --> accentua però il consumo del bordino e della rotaia
Con rotaie bagnate il coefficiente di svio aumenta, perché la maggiore scivolosità riduce la forza di attrito la quale consente l'arrampicamento della ruota lungo la parete laterale del fungo.

Utilizzazione dell'aderenza in trazione

L'aderenza degli pneumatici assume rilevanza

In curva
In frenatura
In trazione

In particolare, in trazione, risulta particolarmente rilevante nei casi di accelerazione in salita.
Trascurando tutte le resistenze naturali al moto, la forza di trazione applicata alle ruote motrici deve equilibrare, a velocità costante, la componente della gravità parallela alla via.

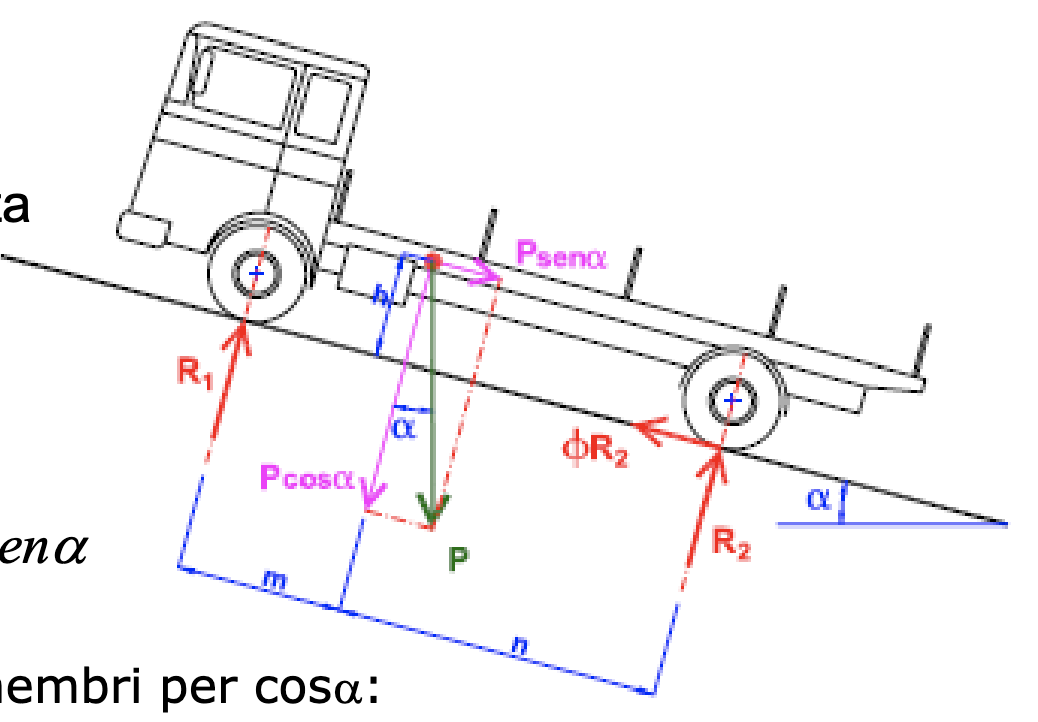
TRAZIONE POSTERIORE
Nella condizione di limite con trazione posteriore:

R_{2} (m + n) = h \cdot P \sin α + m \cdot P \cos α

che diventa:

R_{2} = \frac{h \cdot P \sin α + m \cdot P \cos α}{m + n}

Al limite di aderenza

φ \cdot R_{2} = P \cdot \sin α

e quindi, sostituendo

φ \frac{h \cdot P \sin α + m \cdot P \cos α}{m + n} = P \sin α

da cui, dividendo per $\cos α$ possiamo trovare la relazione

\tan α = \frac{m φ}{m + n - φ \cdot h}

e quindi:

Se aumenta l'altezza del baricentro ( $h$ ), la pendenza limite aumenta
Se aumenta la distanza tra baricentro e ruote motrici ( $m$ ), dato un certo passo $p$ , la pendenza limite si riduce
Se aumenta il coefficiente di aderenza $φ$ , la pendenza limite aumenta

Si deve in ogni caso verificare la condizione di guidabilità, $R_{1} > 0$

TRAZIONE ANTERIORE
Nel caso di trazione anteriore, si trova che la pendenza limite in condizione di aderenza è

\tan α = \frac{φ (p - m)}{p + φ h}

TRAZIONE INTEGRALE

\tan α = φ

La pendenza massima è indipendente dalla geometria del veicolo
La pendenza limite dipende solo dal coefficiente di aderenza longitudinale $φ$

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ aderenza in trazione con rimorchio
❗❗❗❗❗❗❗❗❗❗❗❗❗

Utilizzazione dell'aderenza in frenatura

Autovettura a 2 assi

Se le forze frenanti fossero esattamente ripartite come i carichi sulle singole ruote, la decelerazione massima ottenibile sarebbe, dato che al limite di aderenza

\frac{P}{g} d = φ P

e quindi la decelerazione massima

d = φ g

Essendo il peso dell'auto non distribuito in modo omogeneo sui due assi, calcoliamo che rapporto c'è tra la forza frenante al limite di aderenza sui due assi.
Questo rapporto, $α$ sarà (si omettono i conti ottenuti tramite l'equilibrio dei momenti):

α = \frac{F_{1}}{F_{2}} = \frac{R_{1}}{R_{2}}

Fissato il coefficiente di aderenza $φ$ bisogna far si che la forza frenante venga ripartita secondo $α$ sui due assi.

Nelle auto tradizionali il rapporto $α$ è fisso e imposto dal costruttore. Nel caso particolare in cui il coefficiente di aderenza incontrato sia effettivamente quello di progetto, si può frenare con tutte le ruote al limite di aderenza. Altrimenti solo uno dei due assi sarà al limite di aderenza, mentre l'altro si troverà al di sotto.

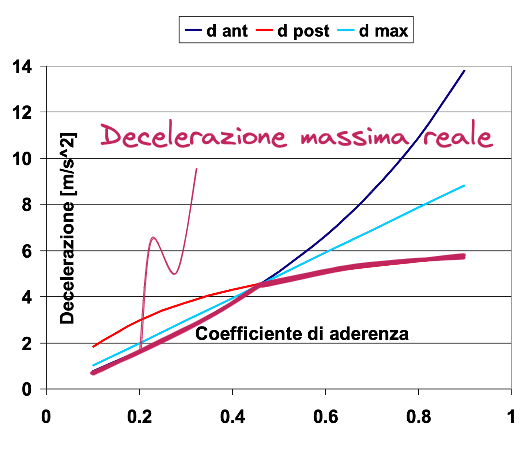
In celeste è mostrato l'andamento della decelerazione massima idealmente ottenibile quando il coefficiente di aderenza reale ( $φ$ ) coincide con quello di progetto ( $φ_{p}$ )

$φ < φ_{p}$ - decelerazione limitata dall'asse posteriore: slitta prima
$φ > φ_{p}$ - decelerazione limitata dall'asse anteriore

Nella realtà quindi la decelerazione effettiva risulta sempre minore rispetto alla teorica massima ottenibile.

Per ovviare a questo problema ci sono dispositivi che modificano dinamicamente il rapporto di frenatura.

Un ulteriore problema è dovuto allo squilibrio dei carichi generato dal rallentamento delle masse rotanti. Anche l'enegia di queste masse va dissipata dai freni. Non ha effetto sull'aderenza ma per l'equilibrio va considerata nel calcolo di $α$ .

[?] Il pendolante, trascurando il problema dell'interoperabilità dell'infrastruttura, permetterebbe sovralzi maggiori?
Vedere deragliamento AV Spagna (santiago de compostela)

metropolitana di norimberga, automatica, non ha le porte di banchina ma ha laser che individuano ostacoli sui binari e mandano in frenatura il treno.

[?] Stiamo lavorando sempre senza altre resistenza?

4. Dinamica dei Veicoli - VIT, page 10
Passando da rettilineo (acc centripeta = 0), in curva c'è accelarazione. Se passiamo direttamente in curva avremmo una variazione di acc. nel tempo praticmaente infinito portando a disconfort molto alto. Il raggio della curva a livello planimetrico non è direttamente pari a R ma passa gradualmente.
Ci sono dei raccordi planimetrici. In ambito stradale di solito si usa la clodoide. In campo ferroviario la parabola cubica.
Nel caso ferroviario servirebbe anche un raccordo altimetrico per raccordare il sovralzo.
In ferrovia si sfrutta il raccordo per variare sia la curvatura che il sovralzo.