01 - Introduzione - VIT

L'obiettivo di Veicoli e Impianti di Trasporto è di fornire le conoscenze teoriche di base relative sia all'architettura, la dinamica e la locomozione dei veicoli utilizzati nei sistemi di trasporto terrestri.

veicolo

Per veicolo si intende qualunque contenitore mobile in grado di trasportare passeggeri o merci (funzione commerciale).

La mobilità è garantita da un sistema di locomozione completamente o parzialmente a bordo (veicolo automotore) ovvero dalla possibilità di essere trainato da veicoli automotori.

Non tratteremo i veicoli per lo svolgimento di lavori di altra natura (veicoli speciali)

Il veicolo è un sistema costituito da diversi sottosistemi:

Sostentazione
Guida - libera o vincolata
Locomozione - che assicura la realizzazione del moto
Controllo della marcia - manuale, automatico e vie di mezzo: semiautomazione

Si può avere:

Trazione concentrata
Trazione distribuita
- Risolve il problema dell'aderenza limitato tra ogni ruota e binario

Classificazione dei sistemi di trasporto

#Classificazione per sostentazione
#Classificazione per locomozione
#Classificazione per guida
#Classificazione per controllo di marcia

Classificazione per sostentazione

sostentazione

La sostentazione è la funzione che consente al veicolo di scambiare le forze con l'ambiente esterno.

È sostanzialmente di 3 tipi:

#Sostentazione statica
#Sostentazione dinamica
#Levitazione magnetica

Sostentazione statica

sostentazione statica

Non è necessaria energia per garantire la sostentazione. Non è necessario moto relativo tra ambiente e veicolo.

Ad esempio veicoli terrestri, natanti, veicoli aerei a sostentazione aerostatica (dirigibile, mongolfiera...)

Sostentazione dinamica

sostentazione dinamica

La Sostentazione dinamica è quella realizzata attraverso un moto relativo tra veicolo e fluido ambiente con produzione di energia cinetica

Spinta Idrodinamica: aliscafo
Spinta aerodinamica
Gettosostentazione
- Esoreattori: se prende parte il fluido ambiente
- Endoreattori: se non prende parte il fluido ambiente (razzo)
- Hovercraft: getti freddi opportunamente intubati
  - 2 eliche:
    - Una con asse orizzontale che serve alla propulsione
    - Una con asse verticale che solleva il veicolo dal suolo

Levitazione magnetica

sostentazione magnetica

Nella sostentazione magnetica la sostentazione è realizzata attraverso lo scambio di forze di natura elettromagnetica tra il veicolo e la pista.

Veicolo a levitazione magnetica: detti anche maglev.

La sapienza li studia nell'ambito del DITS: in un progetto europeo "Made 4 Rail"
vd. Nevomo.

Classificazione per locomozione

locomozione

La locomozione è la funzione che realizza il moto vincendo le forze che a esse si oppongono (resistenze al moto).

Si utilizza un propulsore che utilizza l'energia meccanica trasmessa dal motore che a sua volta ottiene da energia termica o elettrica.

Si avranno:

Ruote motrici: quelle locomotrici
Ruote trainate
Traino con fune (funivie, seggiovie, funicolari)
Cremagliera (treni a cremagliera: vanno su salite molto ripide)
- Fra le due rotaie c'è una dentiera che ingrana con una ruota dentata montata sul treno
Elica (natanti, aeromobili)
Esoreattore (Aeromobili, missili)
Endoreattore (razzi)
Motore lineare (maglev)

Classificazione per guida

guida

La guida è la funzione che consente al veicolo di seguire la traiettoria voluta.

#Guida libera
#Guida vincolata

Guida libera

La traiettoria è imposta dal conducente (es. automobile)

Ad esempio l'auto ha 2 gradi di libertà.

Guida vincolata

La traiettoria è imposta dall'infrastruttura (ferrovia).
Ha 1 solo grado di libertà

Classificazione per controllo di marcia

Controlla sia la locomozione che la guida.

Di 3 tipi:

manuale
#Automatico
#Semi-automatico

Manuale

Unicamente affidato al conducente

Automatico

Conducente completamente assente

Semi-automatico

Treni: Sistemi di protezione:

SCMT: Sistema Controllo Marcia Treno (sistema italiano)
ERTMS/ETCS a diversi livelli: Integrato a livello europeo.
- Liv2: i segnali arrivano direttamente in cabina di guida
- Liv3: distanziamento dinamico non per sezioni di blocco ma basato su posizione, velocità del treno... (si basa sul segnalamento satellitare)

I sistemi di protezione e controllo dei treni devono essere certificati come SIL4. Deve esserci probabilità di guasto minore di $10^{- 9}$ per ora di funzionamento.

Impianti di trasporto

Gli Impianti di trasporto sono l'interfaccia fra il veicolo e le funzioni connesse con il suo uso

Impianti per il trasbordo dei passeggeri: fermate (non c'è possibilità di precedenza), stazioni
Impianti per trasbordo delle merci: stazioni, interporto (scambio fra gomma e ferro)
Impianti per la composizione di treni e veicoli: smistamenti (strutture per fare la composizione dei treni merci: (video)
Impianti per la sosta
Impianti per la manutenzione: depositi, officine
Impianti di manovra e trasbordo di veicoli da una modalità di trasporto all'altra e gli annessi veicoli necessari per l'effettuazione delle manovre
Impianti per la fornitura dell'energia necessaria per la locomozione
Impianti di controllo della marcia del singolo veicolo
Impianti di controllo della marcia di flotte di veicoli e quindi del deflusso veicolare

La ruota

Che la guida sia #Guida libera o #Guida vincolata, l'elemento essenziale a trasmettere gli sforzi di #sostentazione, #Classificazione per guida e locomozione è la ruota.

Cinematica della ruota indeformabile

In prima approssimazione si considera la ruota come un cerchio rigido di diametro $D$ . Si trascurano quindi le deformazioni della ruota e della via (del terreno su cui poggia). Si suppone anche che la ruota percorra una traiettoria lungo una retta e che abbia un singolo punto di contatto col terreno.

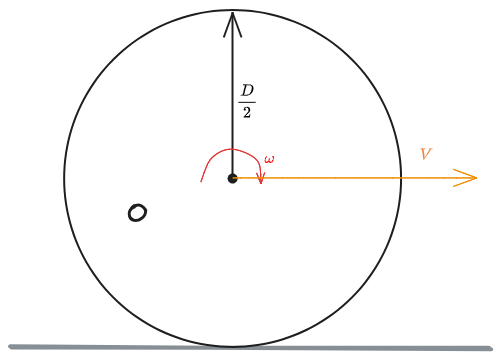
Rotazione intorno al centro $O$ a velocità angolare $ω$ e traslazione a velocità $V$

3 casi possibili:

#Puro rotolamento
#Strisciamento retrogrado
#Strisciamento diretto

Puro rotolamento

Ciascun punto $P$ all'interno della ruota, ruota con velocità angolare $ω$ e trasla nello spazio rispetto a O a velocità $V = ω \overset{―}{O P}$ parallelamente alla via.

Il moto di ogni punto è quindi costituito da due moti:

Rotazione intorno ad O con velocità risultante $ω \overset{―}{O P}$
Traslazione rispetto alla via a velocità $V = ω \frac{D}{2}$
In definitiva ogni punto rispetto al suolo ha istantaneamente come velocità:

V_{T O T} = V + ω \overset{―}{O P}

che risulta nel diagramma triangolare a destra.

$I$ è il centro di istantanea rotazione e risulta fermo rispetto al suolo

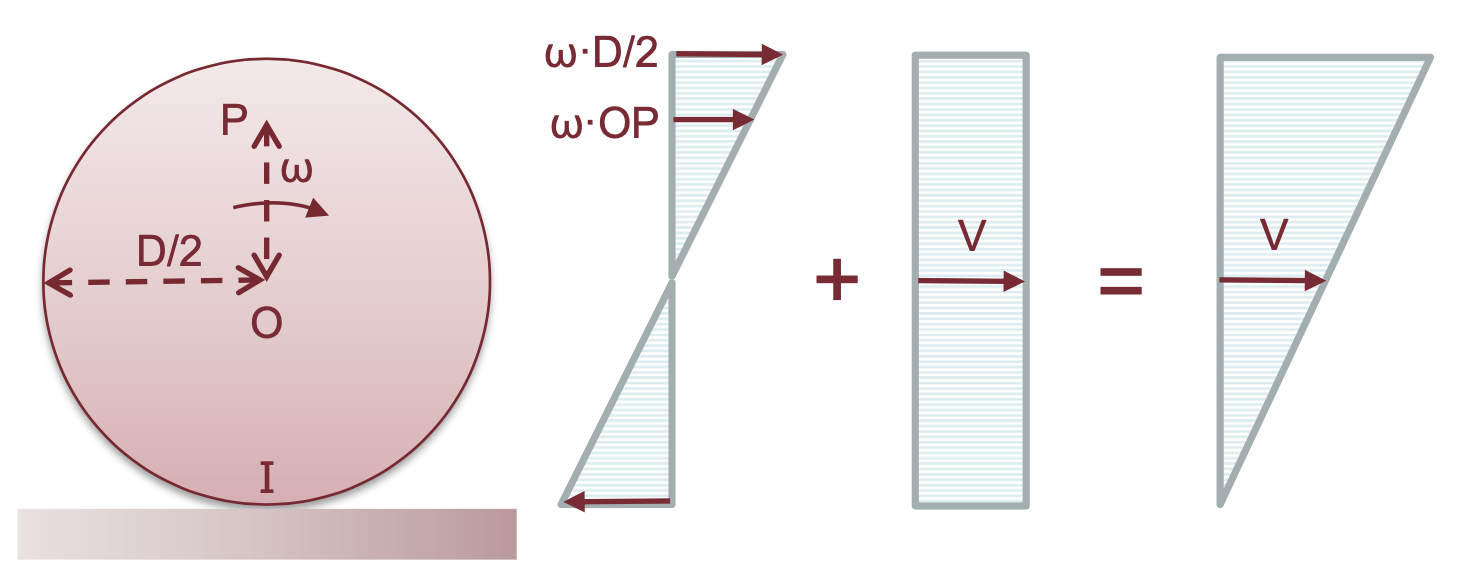
Strisciamento retrogrado

È il caso in cui $V < ω \frac{D}{2}$
In questo caso il punto I a velocità nulla risulta interno al cerchio.
Il punto di contatto invece risulta avere istantaneamente velocità contraria al moto (rispetto alla via) e pari a

ω \frac{D}{2} - V

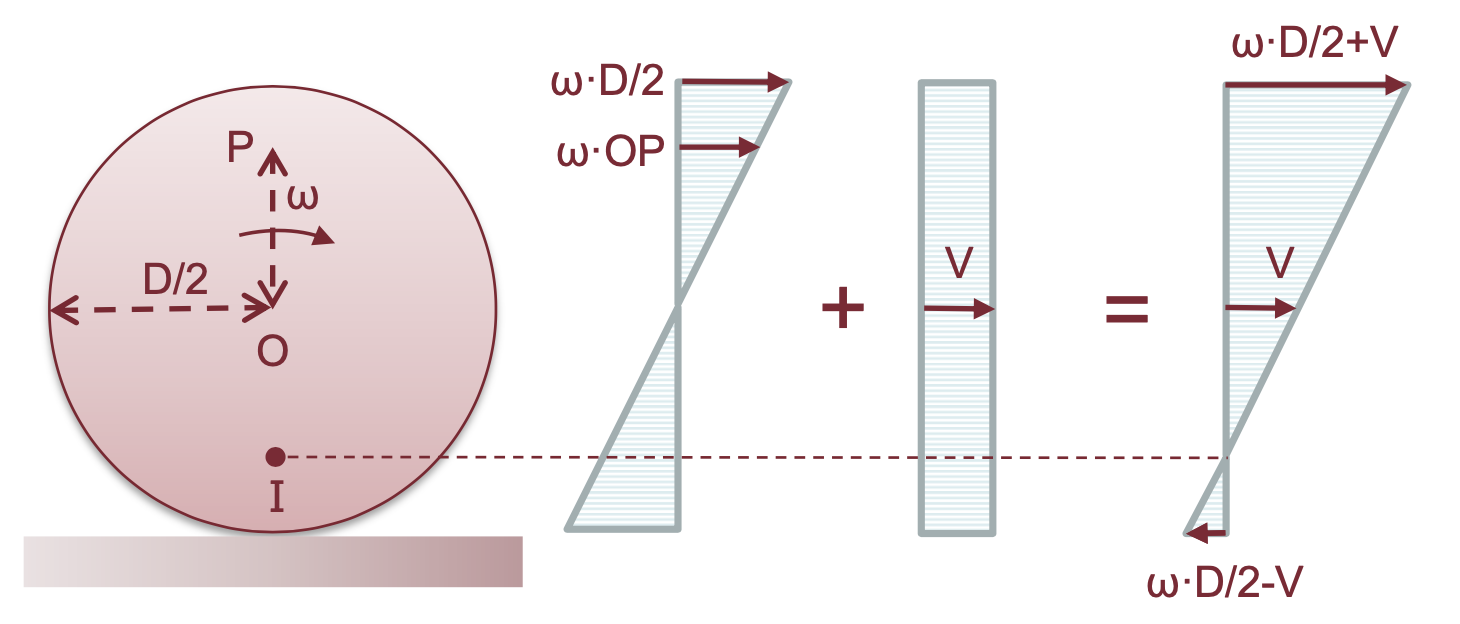
La ruota rotola più che avanzare
(slittamento)

Strisciamento diretto

In questo caso $V > ω \frac{D}{2}$

Il centro di istantanea rotazione I è esterno al cerchio.
Il punto di contatto striscia rispetto alla via con velocità diretta come quella del moto della ruota e a velocità

V - ω \frac{D}{2}

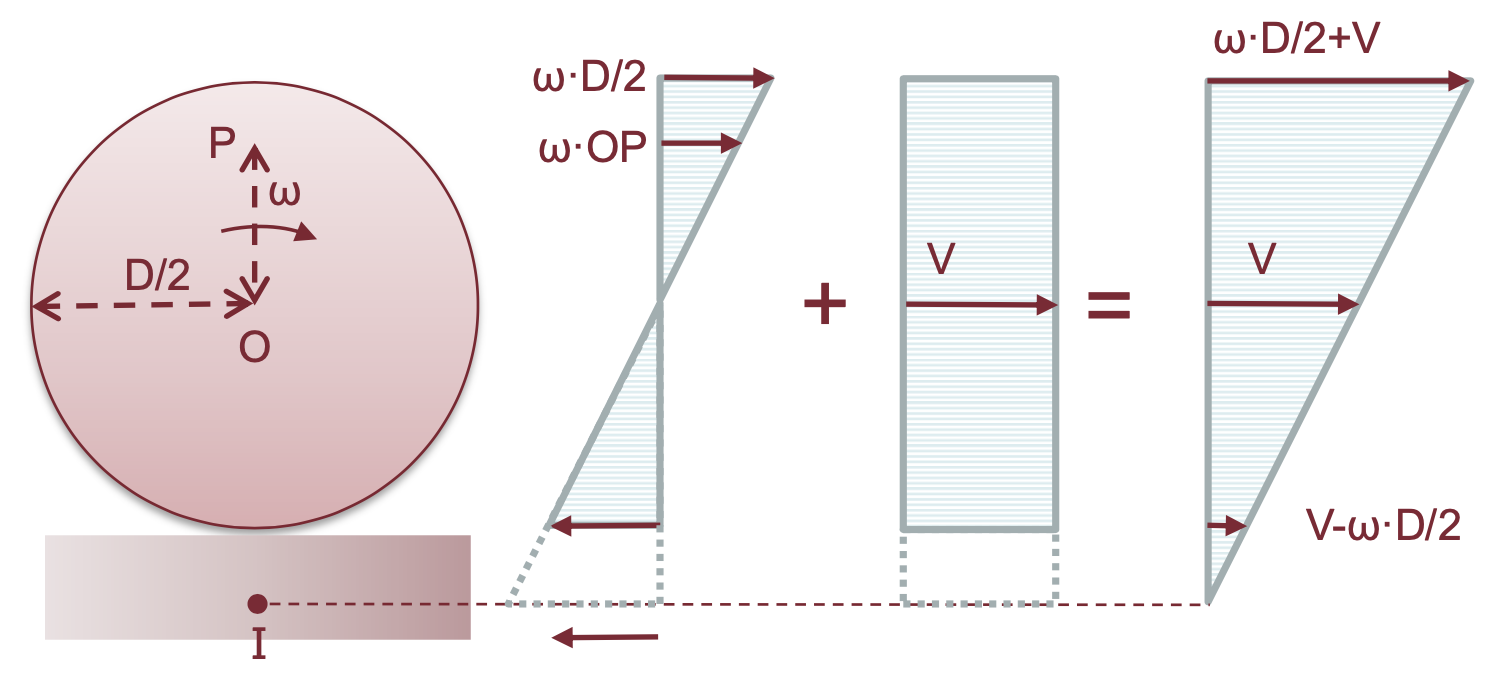
il punto di contatto tra la ruota e il terreno ha una velocità relativa rispetto all'asfalto o al terreno positiva.
(pattinamento)

Scorrimento

Quantifica la ripartizione tra il moto di #Puro rotolamento e lo strisciamento

s = \frac{Spazio percorso in assenza di strisciamento - Spazio effettivo percorso in presenza di strisciamento}{Spazio percorso in assenza di strisciamento}

s = \frac{2 π n \frac{D}{2} t - 2 π n O I t}{2 π n \frac{D}{2} t} = \frac{\frac{D}{2} - O I}{D} = 1 - \frac{2 \overset{―}{O I}}{D}

$\frac{D}{2} = O I ⟹ s = 0$ : assenza di strisciamento (#Puro rotolamento)
$\frac{D}{2} > O I ⟹ s > 0$ : arrivando al valore massimo di 1 quando $I == O$ (ruota che rotola su se stessa senza anvanzare e quindi $V = 0$ : #Strisciamento retrogrado o slittamento)
$\frac{D}{2} < O I ⟹ s < 0$ : arrivando al limite a $- \infty$ quando $\overset{―}{O I} = \infty$ e quindi $ω = 0$ : la ruota striscia senza rotolare (#Strisciamento diretto)

Nell'ultimo caso, per evitare di avere valori negativi di $s$ , si usa una formula leggermente diversa

\begin{aligned} s & = \frac{Spazio effettivo percorso in presenza di strisciamento - Spazio percorso in assenza di strisciamento}{Spazio effettivo percorso in presenza di strisciamento} \\ s & = \frac{2 π n O I t - 2 π n \frac{D}{2}}{2 π n O I t} = \frac{\overset{―}{O I} - \frac{D}{2}}{\overset{―}{O I}} = 1 - \frac{D}{2 \overset{―}{O I}} \end{aligned}

0 \leq s \leq 1

$O I$ : Raggio effettivo di rotolamento
$R$ : Raggio teorico di rotolamento

Lo scorrimento può essere anche espresso in termini percentuali:

s_{%} = s \cdot 100

Statica e dinamica della ruota deformabile elasticamente

Nella realtà, ruota e via sono costituiti da materiali deformabili in presenza di carichi esterni.
Sia ruota che via lavorano in campo elastico.

Per semplificare la modellazione del fenomeno, si può considerare la ruota deformabile poggiata su una superficie (la via) indeformabile. Il campo di pressione che ne risulta è mostrato nella figura sottostante. La pressione è proporzionale all'accorciamento di ciascuna fibra. Si avrà pertanto pressione massima al centro della sezione (segmento nel piano) AC. L'andamento è di tipo parabolico.

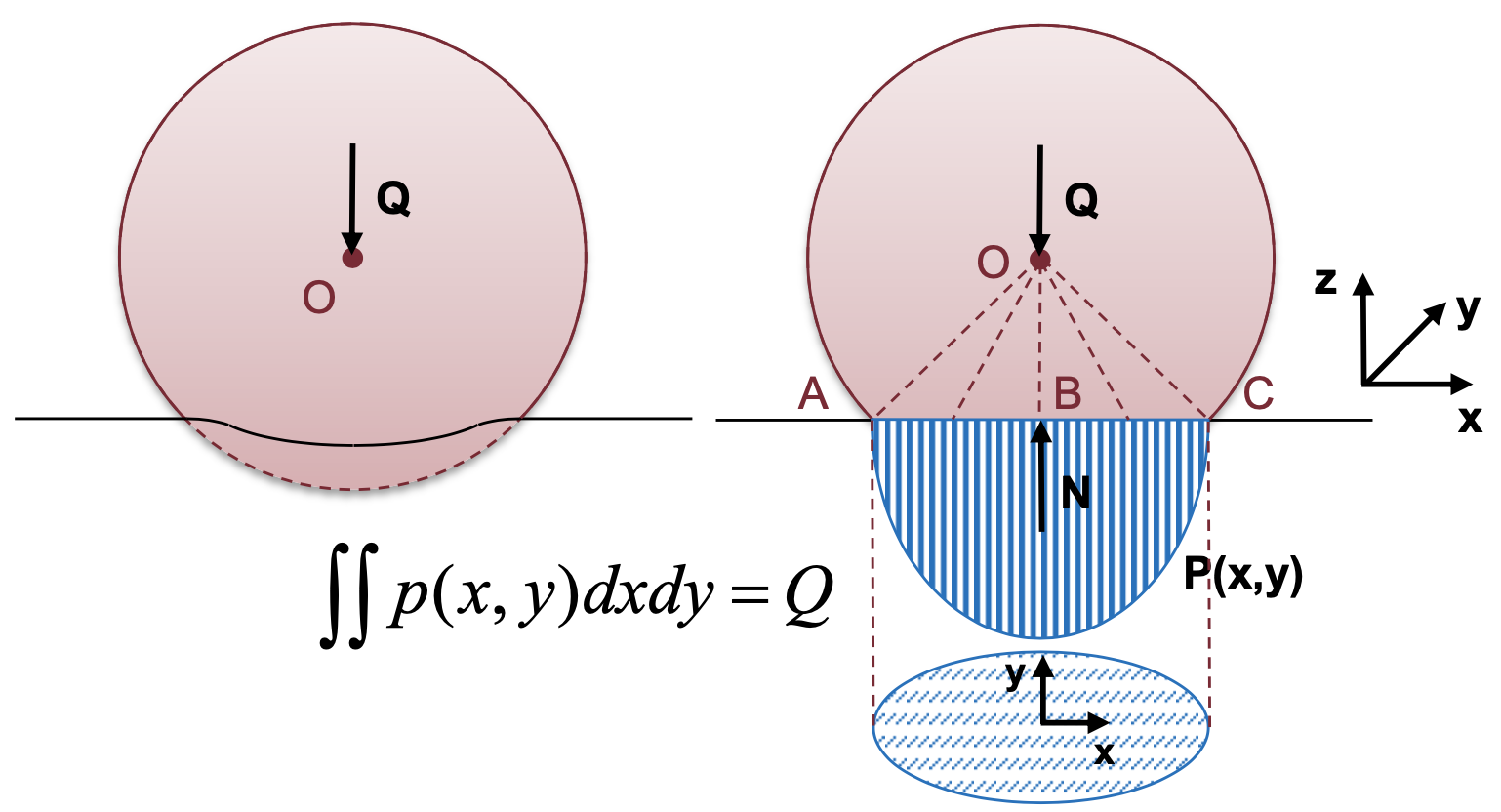
Il totale della forza sarà dato da l'integrale doppio della superficie di contatto ruota-via

Q = \iint p (x, y) d x d y

Per via della deformabilità, tra ruota e via si generano due tipi di resistenze:

#Attrito volvente
#Aderenza
#Attrito radente

Attrito volvente

Per mettere in moto la ruota occorrerà applicare un momento tale da scavallare il bordo della superficie di contatto (A o C). Questo fa sì che il campo delle pressioni si modifichi concentrandosi verso la direzione del moto e facendo sì che la reazione $N$ sia spostata in avanti di una quantità $u$ . Per mettere in rotazione la ruota occorrerà quindi applicare un momento

M = Q u

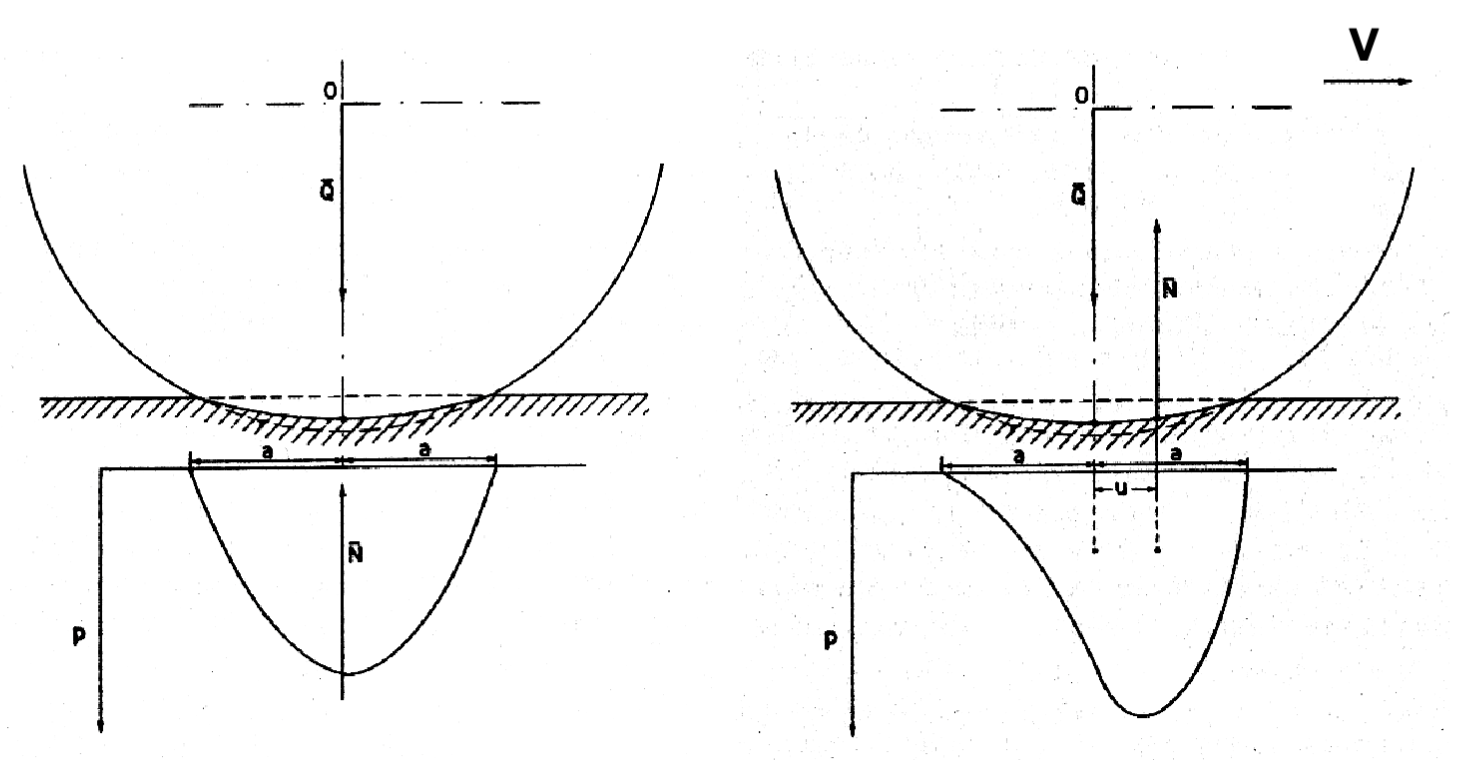
Tale momento si può applicare in due modi:

Applicando un momento torcente all'asse della ruota, $M = Q u = N u$
Oppure applicando al mozzo della ruota una forza $F$ attraverso la boccola tale che sia $F \frac{D}{2} = N u$ essendo $\frac{D}{2}$ il raggio nominale di rotolamento della ruota
si deve in definitiva avere una forza di trazione $F$

F = N \cdot 2 \frac{u}{D}

dove il termine costante $2 \frac{u}{D}$ prende il nome di #Coefficiente di attrito volvente e rappresenta la resistenza specifica che deve essere vinta per mettere in moto la ruota pesante deformata al contatto.

Aderenza

Se due corpi, A e B sono fermi tra loro, in assenza di slittamenti macroscopici, si può applicare una forza tangente alla superficie di contatto $T$ tale che:

T \leq φ N

La massima forza che si può applicare è $T_{a d e r e n z a}$

T_{a d e r e n z a} = φ N

e $φ$ rappresenta il coefficiente di aderenza

Aderenza sulla ruota portante trainata

Si prenda in considerazione in un veicolo la ruota portante trainata. Su questa agisce una forza di traino $F$ applicata nel centro $O$ che induce quest'ultimo a spostarsi parallelamente alla forza e alla via. I punti di contatto ruota-via rimangono fermi tra loro. Si dice che ruota e via sono in #Aderenza.
Il fatto che i punti di contatto ruota-via rimangano fermi tra loro significa che, nel punto $C$ si è generata una forza di attrito specifica $t$ che equilibria la quota parte $d F$ della forza di traino che si scarica su quel punto (sulla fibra $O C$ ).

Tale forza di attrito può crescere fino al valore massimo $p (x, y) f_{0}$ , essendo $f_{0}$ il coefficiente di attrito di primo distacco al contatto ruota-via.

La generica fibra si inflette per consentire lo spostamento relativo che l'attrito di primo distacco impedisce tale inflessione provoca una forza tangenziale elastica $t (x, y)$ (di taglio) al contatto. Questa va confrontata ed equilibrata con la forza tangenziale effettivamente disponibile:

t (x, y) \leq p (x, y) f_{0}

Finché tale condizione è rispettata, si ha solo deformazione elastica senza scorrimento.

Quando invece si verifica

t (x, y) > p (x, y) f_{0}

la condizione di #Aderenza non è più rispettata e il punto di contatto striscia. Pertanto ci sarà attrito pari a

t = p f_{c}

essendo $f_{c}$ il #coefficiente di attrito cinetico.

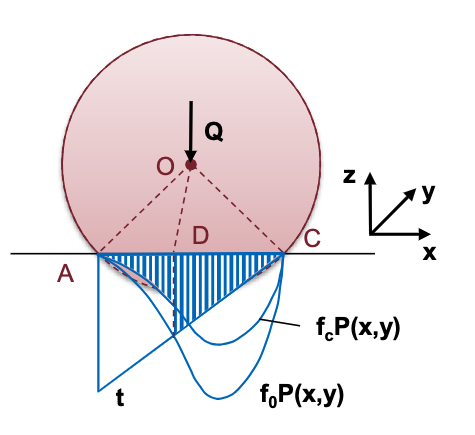
Nella generica sezione longitudinale $\overset{―}{A C}$ dell'area di contatto, ci sarà-

una zona $\overset{―}{C D}$ in attrito statico - la $t (x, y)$ cresce linearmente in presenza di sola deformazione elastica
una zona $\overset{―}{D A}$ in attrito cinetico - la $t (x, y)$ decresce fino al valore limite disponibile pari a $p (x, y) f_{c}$ .

Si avrà quindi che, la forza totale tangenziale al contatto ruota-via presenta due contributi:

Uno generato dalla crescita lineare della forza di taglio nel tratto $\overset{―}{C D}$ - $\iint_{C D} t (x, y) d x d y$
Uno d. to dall'attrito cinetico nella zona di uscita nel tratto $\overset{―}{D A}$ - $\iint_{D A} f_{c} p (x, y) d x d y$
La forza $F$ trasmessa al contatto ruota-via è

F = \iint_{C D} t (x, y) d x d y + \iint_{D A} f_{c} p (x, y) d x d y

Essendo il carico totale dovuto alla distribuzione di pressione pari a $Q$ :

Q = \iint p (x, y) d x d y

In assenza di scorrimento, la massima forza tangenziale che può essere trasmessa è

Q f_{0} = f_{0} \iint p (x, y) d x d y

Se invece tutte le fibre fossero in scorrimento si avrebbe come forza tangenziale

Q f_{c} = f_{c} \iint p (x, y) d x d y

Nel caso in cui siano presenti sia la zona in aderenza che quella in strisciamento, la forza tangenziale $F$ risultante deve necessariamente rispettare la condizione

f_{c} Q \leq F \leq f_{0} Q

e quindi dividendo per $Q$

\begin{aligned} f_{c} \leq & \frac{F}{Q} \leq f_{0} \\ f_{c} \leq & φ \leq f_{0} \end{aligned}

dove $φ$ prende il nome di #Coefficiente di aderenza
La relazione si può anche scrivere, esplicitando le forze:

f_{c} \leq \frac{\iint_{C D} t (x, y) d x d y + \iint_{D A} f_{c} p (x, y) d x d y}{\iint p (x, y) d x d y} \leq f_{0}

Quindi, il coefficiente di aderenza $φ$ effettivamente impegnata può andare da 0 (nessuna forza richiesta) a un valore massimo (che non sarà necessariamente il valore limite relativo all'attrito di primo distacco ma un valore pratico inferiore che assicuri la stabilità del contatto)

Equilibrio della ruota portante e trainata

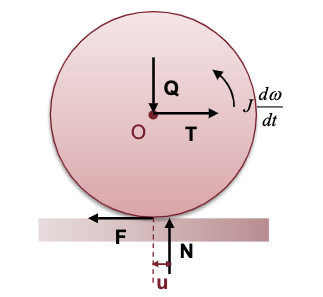
Guardiamo adesso all'equilibrio delle forze e dei momenti sulla ruota portante e trainata.

{\begin{cases} X : & T & = F \\ Y : & Q & = N \\ M_{P} : & T \frac{D}{2} & = N u + J \frac{d ω}{d t} \end{cases}

Affinché la ruota rotoli, occorre vincere l'attrito a rotolamento (#Attrito volvente) ma anche che la forza di contatto sia inferiore a $φ Q$ .

T = F = \frac{2}{D} (N u + J \frac{d ω}{d t}) \leq φ Q

Qualora questa condizione non fosse verificata, la ruota verrebbe trascinata con uno #Scorrimento crescente.
Pertanto al limite la ruota viene trascinata senza rotolare (pattinamento). Si avrebbe quindi raggio effettivo di rotolamento tendente all'infinito e la velocità angolare di rotazione tenderebbe ad annullarsi.

Equilibrio della ruota motrice

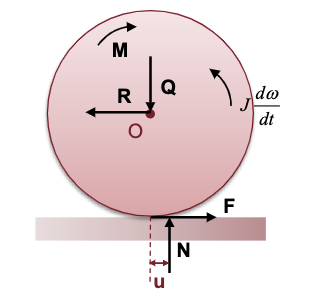
Nel caso di una ruota motrice, al posto di una forza di trazione si ha una coppia motrice $M$ . L'equilibrio in questo caso restituisce:

{\begin{cases} X : R - F = 0 \\ Y : Q - N = 0 \\ M_{P} : M - N u - R \frac{D}{2} - J \frac{d ω}{d t} = 0 \end{cases}

Anche in questo caso vogliamo sia verificata la condizione di aderenza, la quale limita la coppia motrice che può essere applicata.

F = R = \frac{2}{D} (M - N u - J \frac{d ω}{d t}) \leq φ Q

per cui

M \leq φ Q \frac{D}{2} + N u + J \frac{d ω}{d t}

Qualora questa condizione non venisse verificata, la ruota accelererà angolarmente (aumenta $ω$ ) senza però che cresca la sua velocità lineare. Al limite, la ruota rimarrà ferma nello stesso posto girando su se stessa (ruota che slitta).

Equilibrio della ruota frenata

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

Attrito radente

Sono dati due corpi in contatto tra loro in un punto $M$ , in moto relativo a velocità di strisciamento $V$ . L'accoppiamento tra i due corpi è dovuto a una forza normale alle superfici di contatto, $N$ . Ad essa corrisponderà una forza $T$ tangente alle superfici in $M$ e verso opposto alla velocità relativa di strisciamento, pari a:

T = f N

dove $f$ è il coefficiente di attrito.

Coefficienti di aderenza e attrito in funzione alla velocità

In ferrovia, il #Coefficiente di aderenza presenta, a velocità nulla, valori pari a $φ = 0.25 \div 0.35$ a seconda dello stato delle superfici di contatto.
Tale valore decresce al crescere della velocità.
L'andamento del coefficiente di aderenza in funzione della velocità è descritto dalla #Legge di Müller

Legge di Müller

legge di muller

$φ (V) = \frac{φ (0)}{1 + 0.01 \cdot V}$

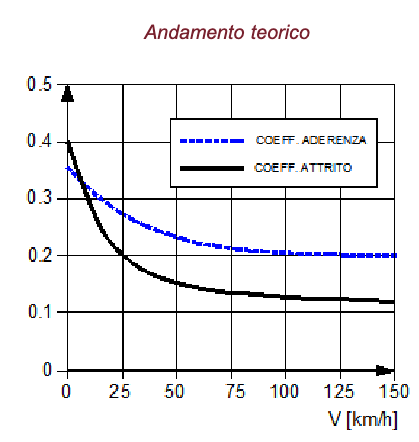
Area di contatto ruota-rotaia

La superficie di contatto tra ruota ferroviaria e rotaia è relativamente limitata. È infatti nell'ordine dei $m m^{2}$ . Varia a seconda del peso, ma in genereale assume valori $200 \div 300 m m^{2}$ per carichi di $5 \div 10 \frac{t o n}{r u o t a}$ .