07. Schematizzazione dell'offerta di trasporto
7. Schematizzazione dell'offerta di trasporto
L'integrazione di più impianti di trasporto lineari e puntuali costituisce una rete.
Rete
Nodo
In una [[#Rete]], i punti di intersezione fra le sedi di traiettoria (vie, linee, rotte) dei veicoli sono denominati nodi.
Si possono considerare nodi:
- i punti di intersezione fra sedi stradali
- i punti di variazione delle caratteristiche dell'infrastruttura
- i punti rappresentativi di luoghi di origine/destinazione della domanda
- si usano per semplificare il problema, accentrando le origini o le destinazioni.
Arco
In una nodi si chiamano archi.
Grafo
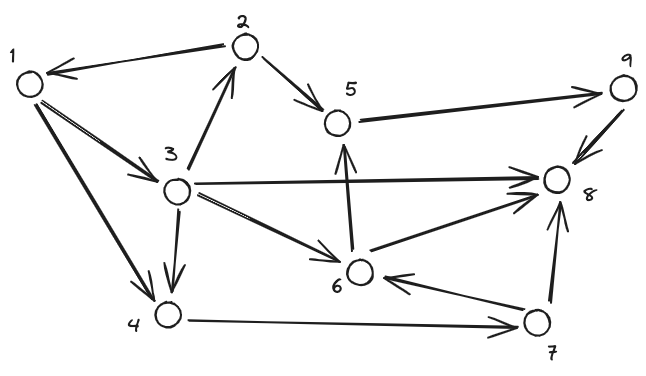
Le reti di trasporto si rappresentano attraverso un grafo, nel quale si riportano le caratteristiche funzionali della rete.
Il grafo è una visualizzazione di tutti i nodi e archi di una rete. Ogni #Nodo è numerato progressivamente e individuato attraverso il numero assegnatogli, mentre gli archi sono identificati attraverso i nodi di estremità.
Quasi sempre si usa più di un modo di trasporto.
A parte l'andare a piedi, ci sono sempre delle combinazioni.
Si accede sempre a piedi.
Il grafo rappresenta reti monomodali o plurimodali.
I grafi plurimodali possono essere combinazione di grafi monomodali
Il grafo si formalizza in una coppia di insiemi
I grafi possono essere o meno orientati:
- Se
allora si dice che il grafo è orientato - Se
allora il grafo non è orientato
Orientamento di un grafo
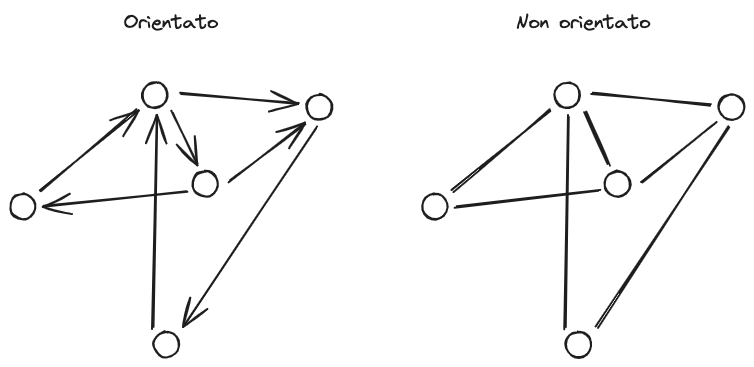
Grafo orientato
In un grafo ordinato, il nodo di partenza è detto Iniziale e quello di arrivo finale.
Grafo non orientato
Un #Grafo si dice non orientato se data una qualsiasi connessione
Si dice anche che le coppie di nodi non sono ordinate.
Connessione di un grafo
Grafo connesso
Grafo non connesso
Un nodi sono raggiungibili in almeno un modo, ovvero se c'è almeno un nodo non raggiungibile.
Completezza di un grafo
Grafo completo
Grafo non completo
Un nodi sono collegati fra loro.
Albero
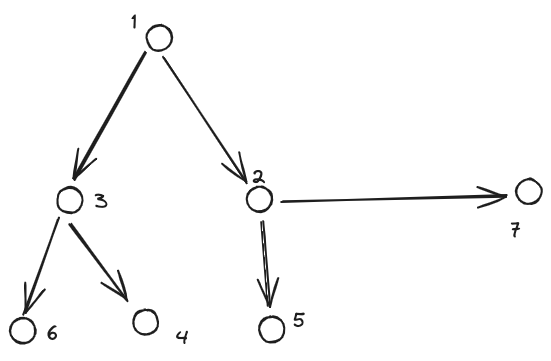
L'albero è un particolare tipo di [[#Grafo]] in cui ogni [[#Nodo]] è raggiungibile da ogni altro [[#Nodo]] mediante un solo itinerario.
Matrice del grafo
Il [[#Grafo]] è uno strumento logico. La rappresentazione grafica è solo uno dei modi. Esistono altri modi che contengono le stesse informazioni.
In particolare, sono utili:
Matrice di adiacenza
La #Matrice del grafo di adiacenza è una matrice che ha come numero di righe e colonne pari al numero di nodi nel [[#Grafo]].
L'elemento
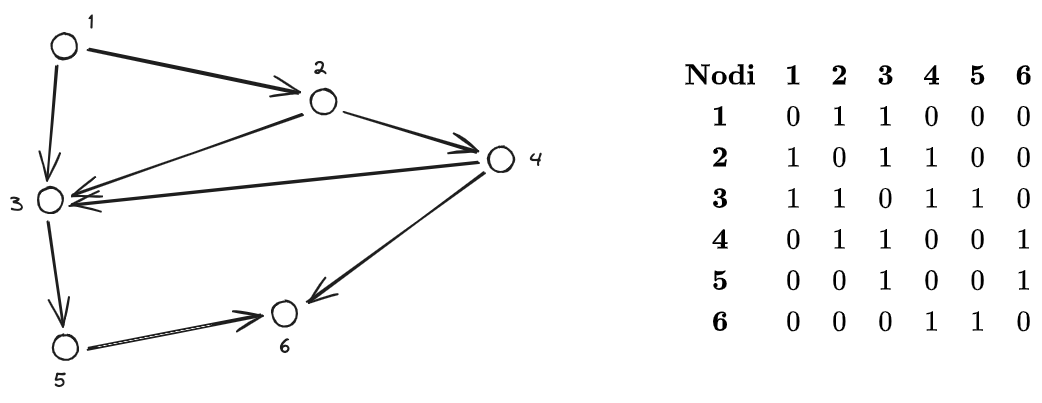
La matrice di adiacenza gode delle seguenti caratteristiche:
- È simmetrica
- Ha tutti 0 sulla diagonale
- È quadrata
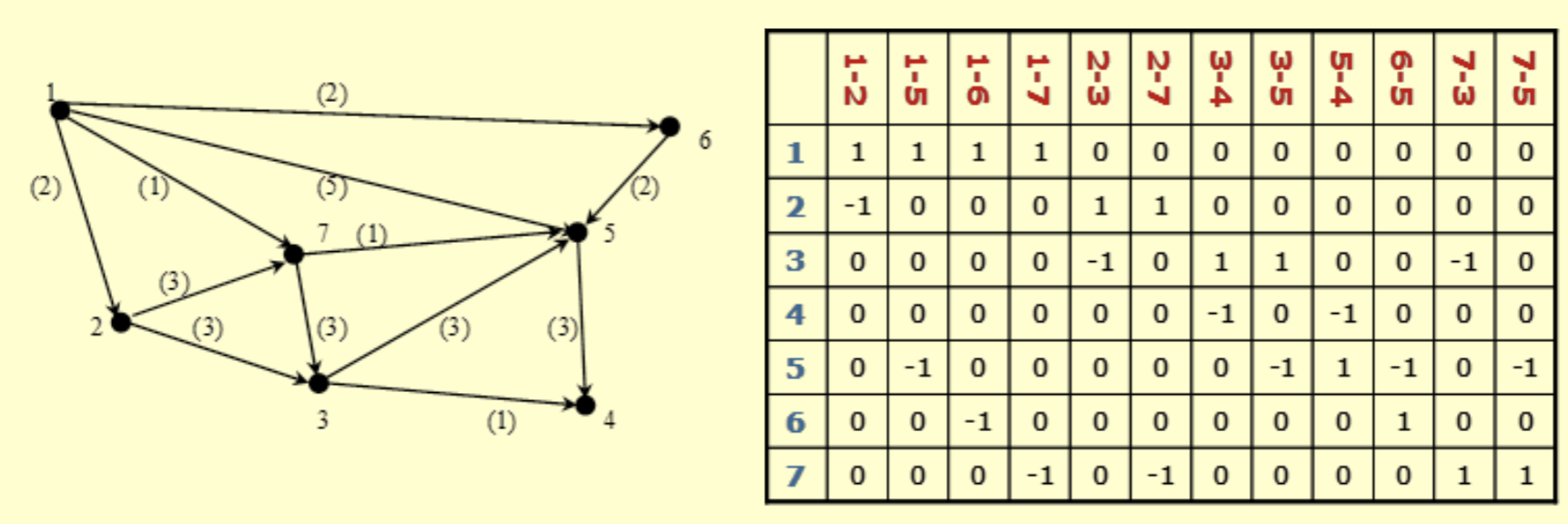
Matrice di incidenza
La #Matrice del grafo di incidenza permette di quantificare - oltre alla connessione tra due nodi, come nella #Matrice di adiacenza - il verso di connessione tra due nodi.
Ogni riga corrisponde a un [[#Nodo]]
Ogni colonna corrisponde a un #Arco
L'elemento
- 0, se il nodo
-esimo non appartiene all'arco della colonna . - 1, se
è il nodo iniziale dell'arco (Arco uscente) - -1, se
è nodo finale dell'arco (Arco entrante)
Impiego del grafo
Dobbiamo associare ad ogni [[#Nodo]] ed ogni [[#Arco]] del [[#Grafo]] una funzione che serva a far capire l'impedenza (la difficoltà ad essere percorso).
Dobbiamo cercare di simulare, cosa succede al sistema se modifico una parte (un nodo o un arco).
Si guarda alla rete come se fosse una rete idraulica o elettrica e se ne calcola l'impedenza. Si cercano poi i percorsi a impedenza minima.
L'impedenza nel nostro campo la chiamiamo: costo generalizzato del trasporto percepito dagli utenti.
Si definisce quindi un percorso/itinerario/cammino = sequenza di archi consecutivi che porta a destinazione
Si individua il cammino minimo fra due poli.
Si chiama linea di desiderio: percorso di minima impedenza complessiva
Linea di desiderio
Si chiama linea di desiderio: percorso di minima impedenza complessiva lungo un [[#Grafo]] nello spostarsi da un [[#Nodo]] all'altro.