05. Teoria del Deflusso

Teoria del Deflusso

Deflusso

deflusso

Il deflusso è la realizzazione degli atti nel tempo

Il flusso è il numero di veicoli che transitano attraverso una certa sezione nell'unità di tempo.

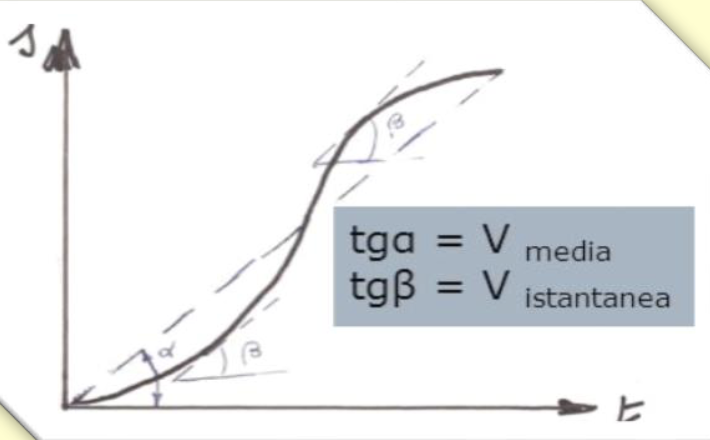
Velocità fittizie

#Velocità commerciale
#Velocità Media

Velocità commerciale

velocità commerciale ($v_{c}$)

È la velocità per andare da A a B comprese le fasi di moto e di sosta.
È data dal totale dello spazio percorso diviso il totale del tempo trascorso.

Velocità Media

velocità media ($v_{m}$)

La velocità media calcolata contando solamente le fasi di moto

Distanziamento

#Distanziamento Spaziale
#Distanziamento Temporale

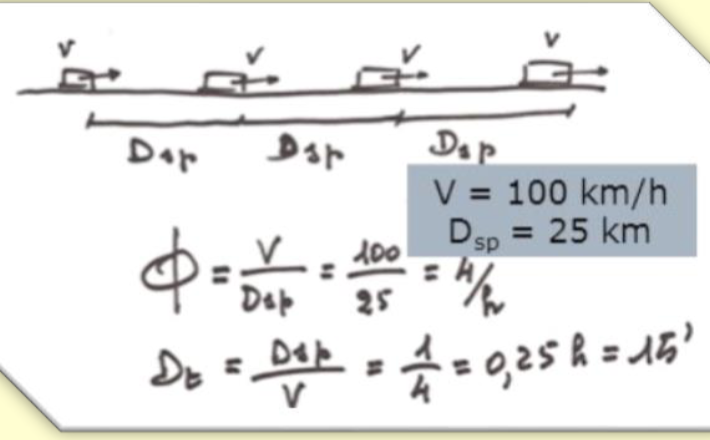
Distanziamento Spaziale

distanziamento spaziale ($d_{\rm sp}$)

Il Distanziamento spaziale è la distanza tra le teste di due veicoli successivi

Distanziamento Temporale

distanziamento temporale ($d_{\rm t}$)

Il distanziamento temporale è il tempo fra il passaggio delle teste di due veicoli successivi attraverso una stessa sezione della loro traiettoria.

Intervallo

L'intervallo è analogo al #Distanziamento ma guarda alla coda del veicolo che precede e alla testa del veicolo che segue.

#Intervallo spaziale
#Intervallo temporale

Intervallo spaziale

intervallo spaziale ($i_{\rm sp}$)

L'Intervallo spaziale è la distanza tra la testa del veicolo che precede e la coda del veicolo che segue.

Intervallo temporale

intervallo temporale ($i_{\rm t}$)

L'intervallo temporale è il tempo fra il passaggio della coda del veicolo che precede e la testa del veicolo che segue attraverso una stessa sezione della loro traiettoria.

Flusso

flusso ($\phi(v)$)

Il flusso è il numero di unità veicolari che transitano attraverso una sezione nell'unità di tempo.

Φ (v) = \frac{v}{d (v)} = v δ (v)

dove:

$δ (v) =$ Densità = inverso del distanziamento
$d (v) =$ #Distanziamento Spaziale

esempio

Schermata 2023-10-16 alle 19.04.47.png|350

Sistema a densità controllata

In un sistema a densità controllata, il #Distanziamento non è libero ma ha valori minimi che non possono essere superati. Il distanziamento è garantito attraverso diversi metodi, alcuni dei quali sono descritti di seguito.

Nell'ambito ferroviario si sono usati diversi tipi di distanziamento.

#Circolazione a Spola
#Circolazione a Bastone Pilota
#Circolazione a Intervallo di Tempo
#Circolazione a Spazio
#Marcia a vista

Circolazione a Spola

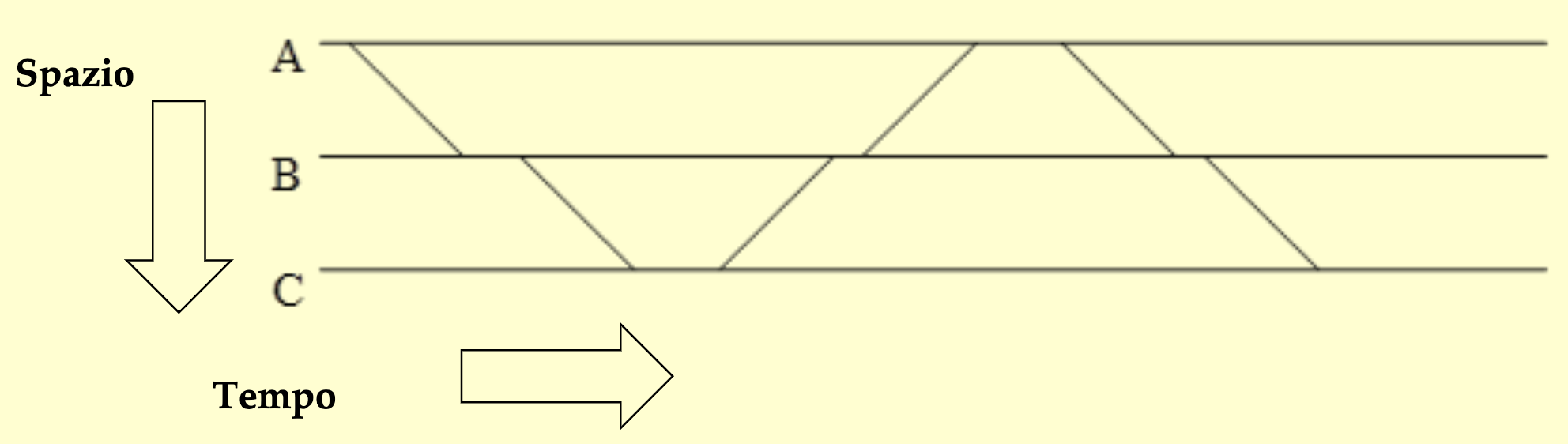
Nei #Sistema a densità controllata la circolazione a spola prevede l'utilizzo di un univo veicolo sull'intera linea. Il [[#Distanziamento]] è automaticamente garantito.

Questo tipo di circolazione è adatta esclusivamente su linee brevi e traffico estremamente modesto.

Circolazione a Bastone Pilota

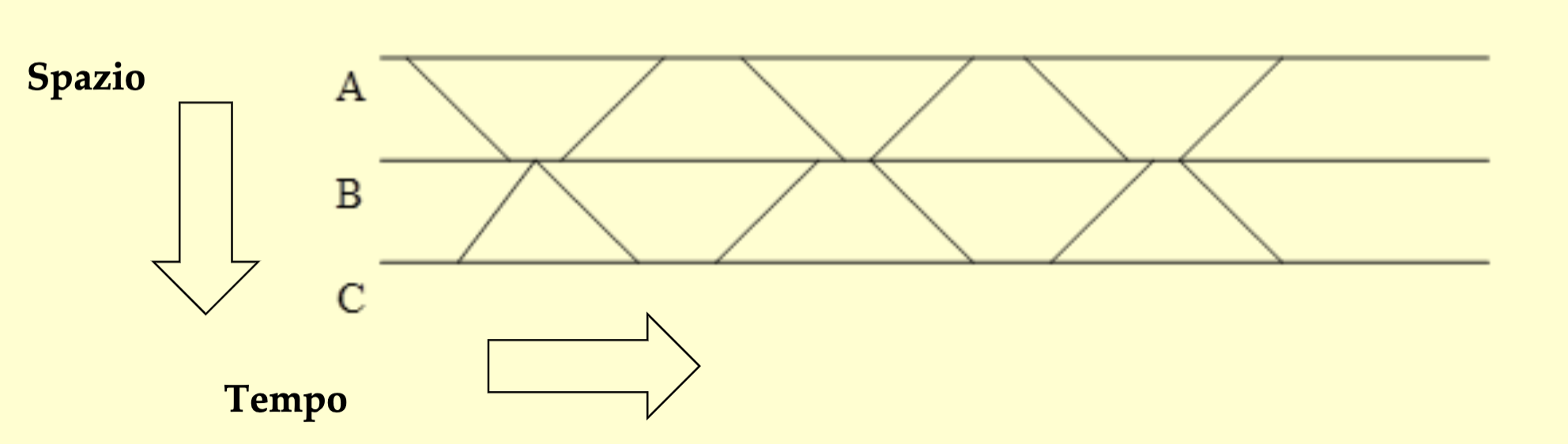
Nei #Sistema a densità controllata la circolazione a Bastone Pilota prevede che ogni macchinista porti con se un medesimo oggetto che viene via via consegnato in ogni stazione. Non si può passare la stazione senza aver ricevuto l'oggetto in questione. Ciò garantisce che tra una stazione e l'altra vi sia sempre un solo veicolo.

Seppur molto sicuro, questo metodo prevede il rallentamento o l'arresto ad ogni stazione, limitando così la capacità della linea.

Circolazione a Intervallo di Tempo

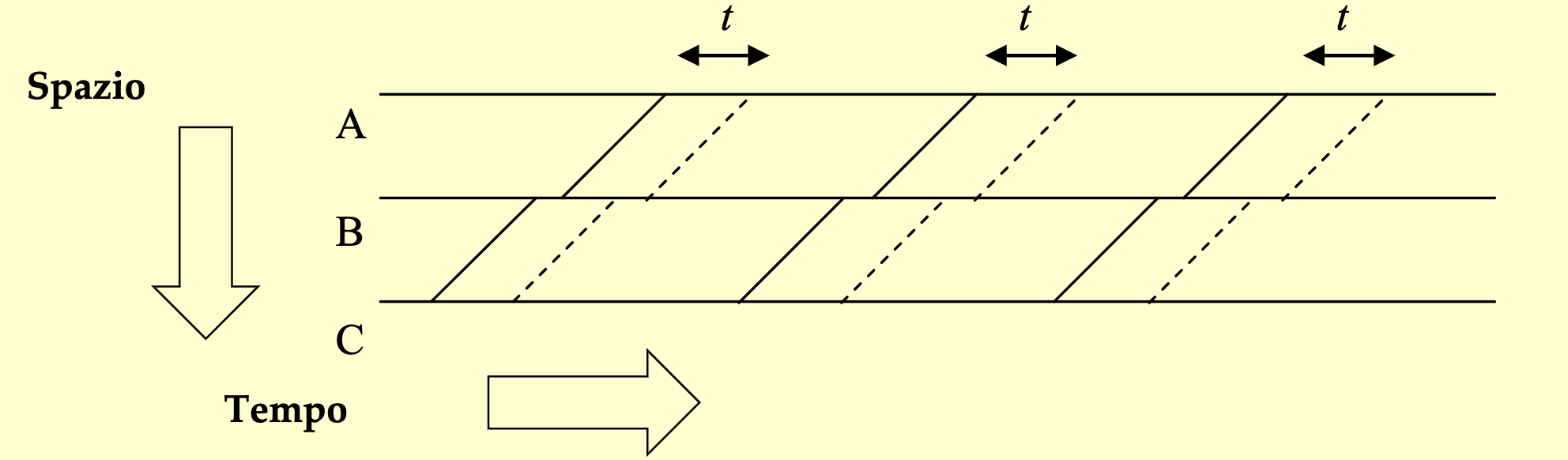
Nei #Sistema a densità controllata la circolazione a intervalli di tempo prevede che ogni sezione in cui è divisa la linea non lasci partire un veicolo fino a quando non sia trascorso un intervalli di tempo $Δ t$ predefinito.

Nonostante la semplicità questo sistema è presto caduto in disuso per la sua bassissima sicurezza. Infatti non teneva conto della variazione della velocità dei convogli in linea o di eventuali rallentamenti imprevisti, come guasti.

Circolazione a Spazio

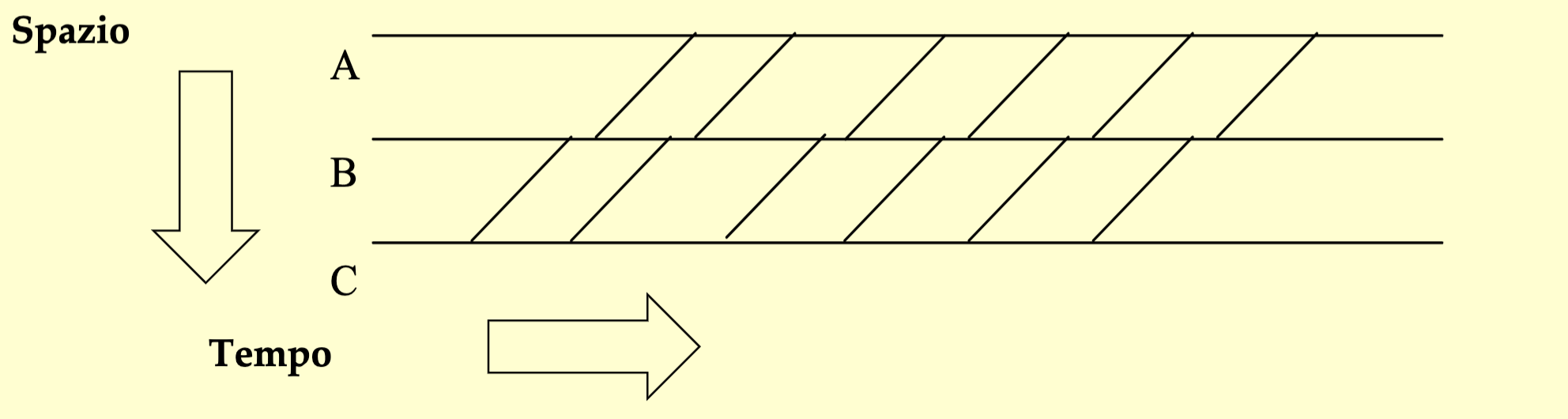
Nei #Sistema a densità controllata oramai si opera quasi sempre con un regime a spazio.
La linea ferroviaria è divisa in sezioni di blocco a lunghezza fissata. All'interno di ogni sezione di blocco deve essere presente un solo treno.
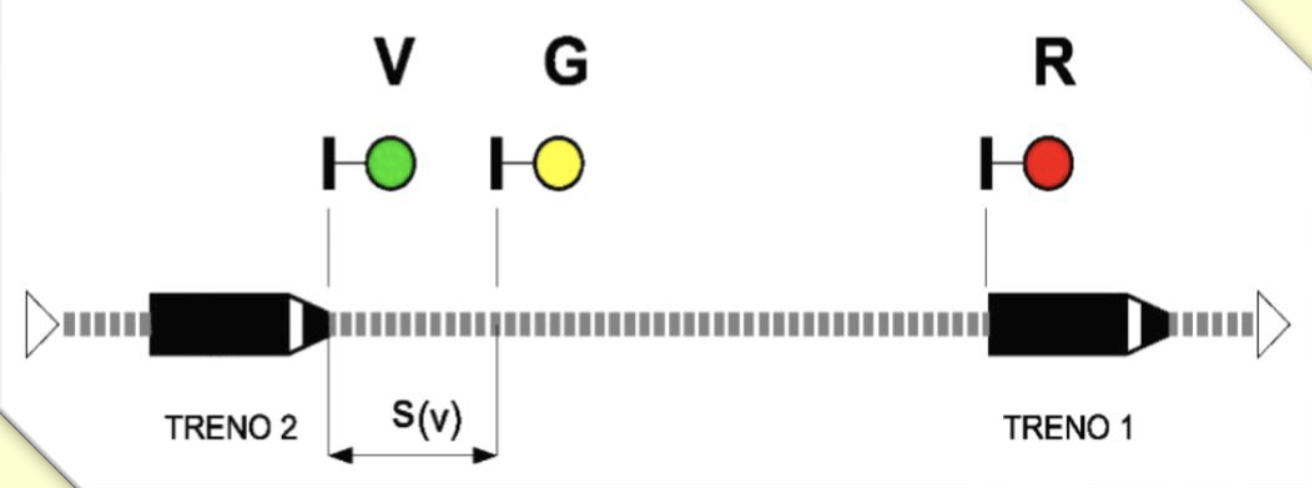
Un sistema di segnali a 2 o 3 aspetti garantisce il distanziamento comunicando al macchinista se la sezione successiva è libera o meno.

Le sezioni sono solitamente di $1500 m$ per linee a velocità massima di $150 \frac{k m}{h}$ ma possono variare in base alla velocità consentita dalla linea.

Marcia a vista

Usata ad esempio nei tram prevede che sia il macchinista a individuare la distanza idonea dal veicolo che precede. La velocità di esercizio dovrà pertanto essere ridotta.

Legge fondamentale del deflusso

Flusso

flusso ($\phi(v)$)

Il flusso è il numero di unità veicolari che transitano attraverso una sezione nell'unità di tempo.

$Φ (v) = \frac{v}{d (v)} = v δ (v)$
dove:

$δ (v) =$ Densità = inverso del distanziamento
$d (v) =$ [[#Distanziamento Spaziale]]

esempio

Schermata 2023-10-16 alle 19.04.47.png|350


Il distanziamento minimo tra due veicoli è dato dalla distanza che impiega il veicolo di coda a fermarsi.

Per un sistema ferroviario si ha che
$$
\phi(v) = \frac{v}{s(v)+\tau v+L}
$$
dove:
- $\tau (v) =$ Tempo di reazione
- $s (v) =$ Spazio di frenatura
- $L =$ Lunghezza del veicolo di testa
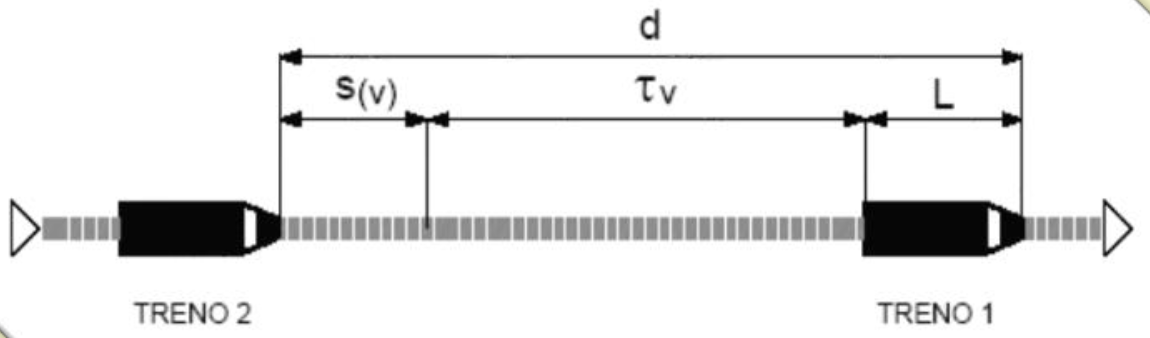
e lo spazio di frenatura è pertanto dato da:
$$
d = \tau(v) + s(v) + L
$$

![Schermata 2023-10-16 alle 19.25.49.png](/img/user/Universit%C3%A0/Triennale/3%C2%B0%20Anno/1%C2%B0%20Semestre/Tecnica%20ed%20Economia%20dei%20Trasporti/Appunti/allegati/Schermata%202023-10-16%20alle%2019.25.49.png)


### Curva di deflusso - densità controllata

In generale possiamo sostituire lo spazio di frenatura con un coefficiente $k$ che dipende dal tipo di distanziamento con cui stiamo operando, rendendo la #Legge fondamentale del deflusso come segue
$$
\Phi = \frac{v}{K \left( \frac{v^{2}}{2a} \right) + \tau(v) + L}
$$
dove:
- $K=$ Un coefficiente dipendente dal sistema di distanziamento
- $a=$ La decelerazione supposta costante
con 
$$
\begin{cases}
K = 1 \qquad \text{Marcia a vista} \\
K = 2 \qquad \text{Per sezioni di blocco protetti da segnali a 3 aspetti}
\end{cases}
$$

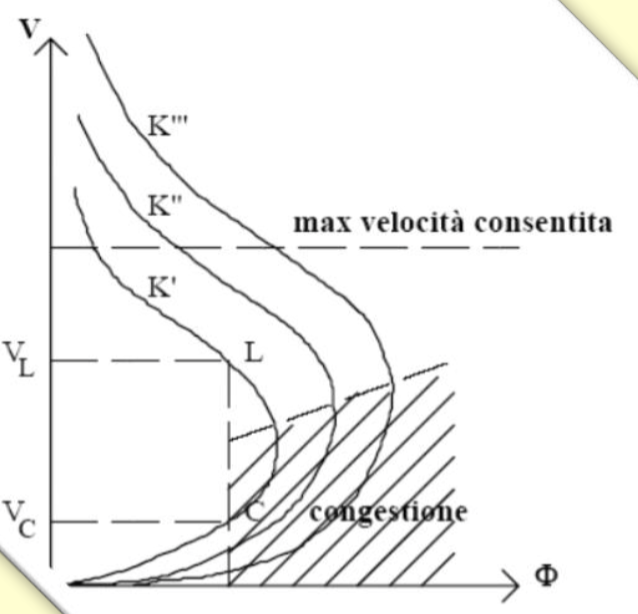
![Schermata 2023-10-16 alle 19.29.17.png|350](/img/user/Universit%C3%A0/Triennale/3%C2%B0%20Anno/1%C2%B0%20Semestre/Tecnica%20ed%20Economia%20dei%20Trasporti/Appunti/allegati/Schermata%202023-10-16%20alle%2019.29.17.png)

All'aumentare di $k$, aumenta anche il flusso.

Se si congiungono i massimi delle curve otteniamo una retta che separa la parte di flusso libero da quella di congestione.

**potenzialità della linea**: il flusso massimo consentito dalla linea



## Sistema a densità libera

Se è vietato il sorpasso, il caso a densità libera (stradale) è assimilabile al caso ferroviario.
In generale però funziona diversamente.
La modellazione è complessa per via di diversi fattori:
- Caratteristiche variabili della strada
- Tipologie di veicoli e composizione variabile
- Caratteristiche e comportamenti dei conducenti imprevedibili
- Condizioni ambientali variabili

È pertanto necessario adottare un **approccio probabilistico** nella modellazione del deflusso.
Per semplificare il processo, si parte da condizioni ideali e si applicano poi dei fattori riduttivi per tenere conto dei fattori di variabilità (condizioni meteo, altimetria, abilità dei conducenti), basati su estese rilevazioni sperimentali.

Il modello più usato è quello proposto nell'Highway Capacity Manual. È americano quindi risente della geometria stradale statunitense e dai loro autisti.

```ad-important
title: Ipotesi

Per tutte le considerazioni che seguono si applicano le seguenti ipotesi:
- Flusso **Stazionario** e **Stabile** (realistico in fasce orarie abbastanza brevi)
- Assenza di veicoli industriali
- Assenza di utenti occasionali o inserperti

Curva di deflusso - Densità libera

Per l'Highway Capacity Manual l'andamento generico del #Flusso in funzione della velocità è come segue.

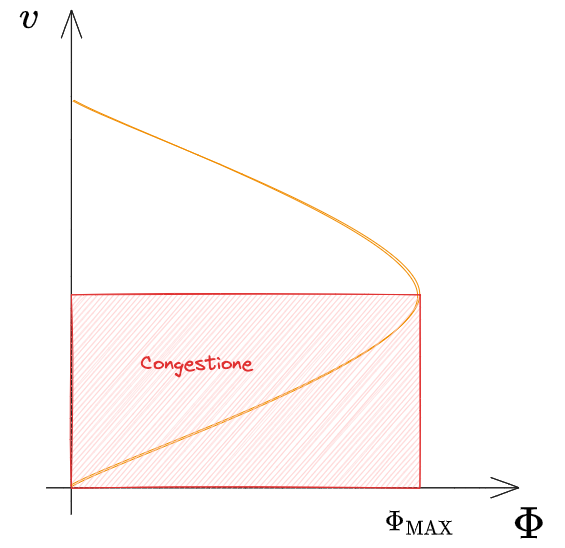
Notiamo che

Alla velocità massima si ha flusso nullo (veicolo isolato)
Il flusso massimo si ha per una velocità intermedia tra la massima e la nulla

Livelli di servizio - LOS

L'Highway Capacity Manual classifica il livello di servizio di un'infrastruttura.
Si va da livelli di servizio migliore a densità basse a livello di servizio peggiori con densità spaziali molto alte.

In particolare si ha:

A - I veicoli si possono muovere comodamente (deflusso libero) con distanziamenti spaziali elevati e i conducenti hanno un elevato comfort di guida
B - Libero/condizionato - I veicoli possono essere talora condizionati (deflusso libero/condizionato) nelle manovre ma non ci sono cadute di livello di servizio dell'infrastruttura
C - Il flusso è nel campo stabile ma i veicoli cominciano ad essere condizionati tra loro (deflusso condizionato); piccoli restringimenti di carreggiata o piccoli aumenti di domanda possono talvolta provocare cadute di livelli di servizio
D - È l'ultimo livello di deflusso stabile; i veicoli sono fortemente condizionati tra loro (deflusso condizionato/congestionato); piccoli incrementi di domanda o piccole riduzioni di offerta provocano senz'altro cadute del livello di servizio
E - Il deflusso funziona su valori prossimi alla capacità (deflusso congestionato) ed evolve rapidamente verso condizioni di instabilità
F - Il deflusso è in condizioni forzate o interrotte ed è caratterizzato da fenomeni cosiddetti stop and go
i vari livelli di servizio sono rappresentati sulla curva di deflusso sottostante:

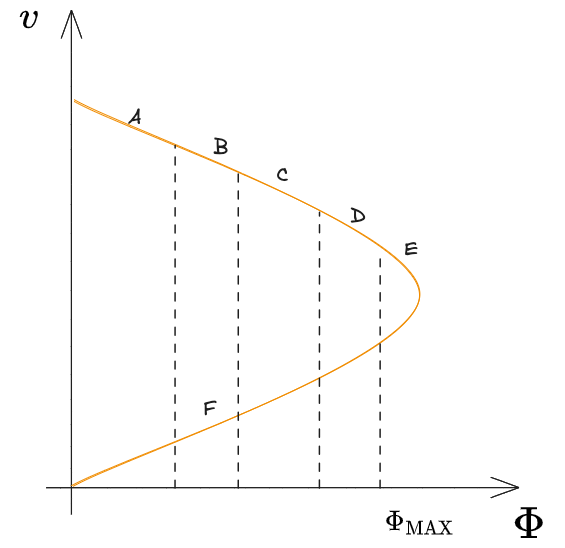
I livelli di servizio possono essere usati per dimensionare un'infrastruttura noto il flusso di utenti che la potrà utilizzare.
Solitamente si usano

Livello B per strade extraurbane
Livello C per strade urbane

Al contrario si possono ricavare i livelli di servizio per verificare il funzionamento di un'infrastruttura esistente.

Deflusso negli impianti puntuali

Determinano la potenzialità dell'infrastruttura più della potenzialità degli impianti lineari in quanto la potenzialità degli impianti puntuali risulta solitamente inferiore a quella degli impianti lineari.
Questo tipo di impianti viene analizzata sotto due aspetti:

La legge di presentazione delle unità veicolari al sistema
I tempi necessari all'effettuazione del servizio richiesto, dipendenti dalle caratteristiche organizzative e di sistema dell'impianto

In generale, quando sia il primo che il secondo punto presentano elementi di aleatorietà, il processo si definisce stocastico e si studia in termini probabilistici.

Possiamo usare modelli:

Analitici - Algoritmi (come la #Teoria delle code)
Analogici - Simulazioni
entrambi dei quali possono essere deterministici oppure aleatori.

La capacità degli impianti puntuali si studia sulla base della teoria delle code.

FLUSSO: Inverso del distanziamento temporale tra due unità veicolari che liberano l'impianto dopo aver ricevuto il servizio.

Flusso massimo: Potenzialità (capacità operativa)
Bisogna quindi definire due leggi:

Legge A - #Legge degli arrivi
Legge S - #Legge dei servizi
Possibili leggi degli arrivi:
Tempi uguali: orario cadenzato in regime non perturbato (tipo metropolitana)
Tempi diseguali ma determinati: orario libero in regime non perturbato (tipo ferrovia ordinaria)
Tempi diseguali ed aleatori: regime perturbato

Processo stocastico

processo stocastico

Il processo si definisce stocastico se almeno una delle due leggi risulta aleatoria.

I processi stocastici si dicono

Processo stocastico Discreto

processo stocastico discreto

Un [[#Processo stocastico]] si dice discreto se il cambiamento di stato avviene in temppi $t_{1}, t_{2}, . . ., t_{n}$ assegnati, non aleatori
Il caso ad esempio delle intersezioni stradali semaforizzate

Processo stocastico Permanente

processo stocastico permanente

Un [[#Processo stocastico]] si dice permanente se il sistema rimane in un certo stato per un certo tempo finito

Processo stocastico Discontinuo

processo stocastico discontinuo

Un [[#Processo stocastico]] si dice discontinuo se ogni cambiamento di stato avviene in un qualsiasi tempo $t$ non assegnato
Il caso ad esempio di un impianto terminale.

Processo stocastico Stazionario

processo stocastico stazionario

Un [[#Processo stocastico]] si dice stazionario se il fenomeno è indipendente dall'origine dei tempi e tali risultano i suoi indici probabilistici.

Legge degli arrivi

Nel campo dei trasporti si considera che gli arrivi siano distribuiti

Individualmente
Collettivamente
a caso.

ipotesi

Processo stazionario - La probabilità $p_{n} (t)$ che si abbiano $n$ eventi fra un istante iniziale 0 e un tempo $t$ non dipende dall'istante iniziale prescelto
Eventi rari - Non si verificano mai 2 eventi nello stesso istante
La probabilità che si verifichi un arrivo in un intervallo $Δ t$ , indipendentemente dal tempo $t$ di riferimento, è pari a $λ Δ t$

Sotto queste ipotesi si può dimostrare che vale la legge di legge di Poisson:

p_{n} (t) = \frac{(λ t)^{n}}{e^{λ t} n!}

dove:

$λ$ è il tasso degli arrivi, ossia il numero di arrivi in un certo intervallo di tempo.
Si fanno un tot di osservazioni, ognuno di un certo periodo di tempo.

λ t = \frac{R}{N}

dove

$R =$ numero tot degli eventi
$N =$ numero di osservazioni di durata $t$

Nella variabile di Poisson la 03. Variabili Aleatorie#Media coincide con la 03. Variabili Aleatorie#Varianza che è uguale a $λ$ .

E = V a r = λ

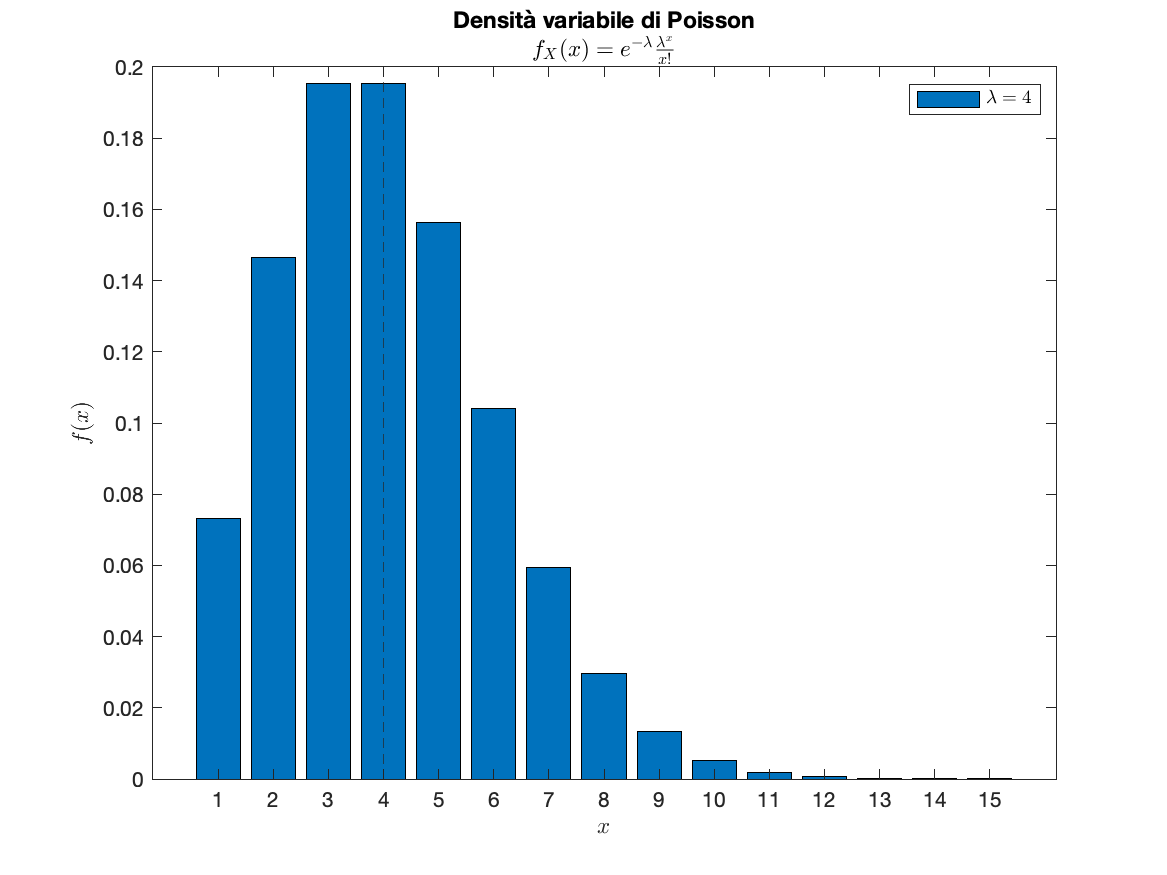
Tasso degli arrivi

Il parametro $λ$ nella #Legge degli arrivi è detto tasso degli arrivi e indica il numero di arrivi nell'unità di tempo.

λ = \frac{R}{N \cdot t}

Legge dei servizi

Occorre ora definire quale sia la legge di distribuzione di erogazione del servizio. Per farlo, si una distribuzione esponenziale.

χ (t) = \frac{1}{T_{m}} e^{- \frac{t}{T_{M}}}

dove:

$T_{m} =$ Durata media dell'occupazione dell'impianto
$μ = \frac{1}{T_{m}} =$ numero medio di unità servite nell'unità di tempo

Tasso delle unità servite

Il parametro $μ$ nella #Legge dei servizi indica il tasso delle unità servite e rappresenta il numero medio di unità servite nell'unità di tempo.

Teoria delle code

A questo punto possiamo iniziare a costruire la così detta Teoria delle code.
Per prima cosa definiamo l'#Intensità di Traffico.

Intensità di Traffico

Si definisce intensità di traffico ( $ψ$ ) il rapporto tra il #Tasso degli arrivi e il #Tasso delle unità servite

ψ = \frac{λ}{μ}

In base al valore di questo rapporto si hanno due casi:

{\begin{cases} ψ < 1 Non si genera coda \\ ψ > 1 La coda cresce a infinito nel tempo \end{cases}

Tenendo conto delle considerazioni fatte fino ad ora, si procede al calcolo delle probabilità di

avere $n$ unità nel sistema (unità in coda + unità servite)
Non attendere (0 unità nel sistema)
Avere fino ad N unità nel sistema
avere più di N unità nel sistema

Probabilità di avere n unità nel sistema

probabilità di avere $n$ unità nel sistema (unità in coda + unità servite)

$P_{n} = {(\frac{λ}{μ})}^{n} [1 - (\frac{λ}{μ})] = ψ^{n} (1 - ψ)$

Probabilità di non attendere

probabilità di non attendere (0 unità nel sistema)

$P_{0} = 1 - ψ$

Probabilità di avere fino ad N unità nel sistema

probabilità di avere nel sistema fino a $n$ unità

$n < N$

$\sum_{n = 0}^{N} P_{n} = \sum_{n = 0} ψ^{n} (1 - ψ) = 1 - ψ^{N + 1}$

Probabilità di avere più di N unità nel sistema

probabilità di avere più di $n$ unità nel sistema

$\sum_{n = N + 1}^{\infty} P_{n} = 1 - (1 - ψ^{N + 1}) = ψ^{N + 1}$

Numero medio di unità nel sistema

In ogni istante, se $ψ < 1$ si hanno in media nel sistema:

$M (n) = \frac{ψ}{1 - ψ}$

Numero medio di unità in coda

Nonostante possa sembrare controintuitivo, il numero medio di unità nella coda NON è pari a $M (n) - 1$ :

M (n - 1) \neq M (n) - 1

Va calcolato con la definizione di media:

$M (n - 1 \overset{△}{=} ν) \overset{\dots}{=} M (n) ψ$

Deflusso negli impianti puntuali

Il fenomeno del deflusso, negli impianti puntuali, è assai complesso da esprimere e sviluppare analiticamente per varie ragioni

Presenza di regimi transitori
Funzioni di distribuzione di arrivi e/o servizi complesse (non riconducibili a Poisson, Esponenziale...)
Sistemi in cascata (impianti ravvicinati in cui la legge dei servizi del primo influenza la legge degli arrivi del secondo)

Si tende quindi a studiare il fenomeno attraverso delle simulazioni.
In particolare si distinguono due casi

#Simulazione con arrivi frequenti
#Simulazione con arrivi rari

Simulazione con arrivi frequenti

Se si hanno arrivi frequenti, ossia il secondo veicolo arriva quando il primo sta ancora usufruendo del servizio, l'andamento può essere descritto dallo schema sottostante

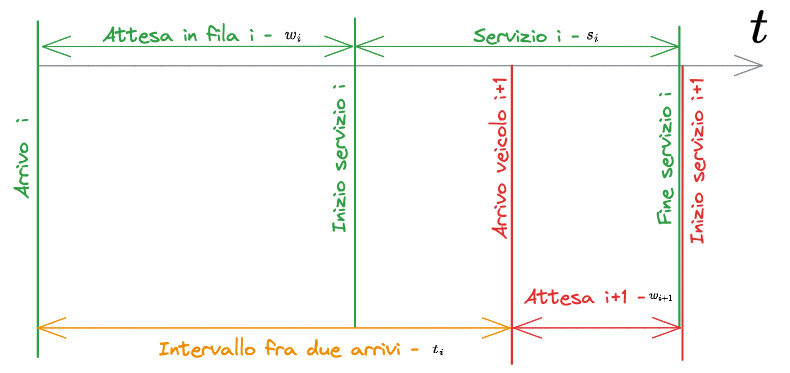
Si hanno

$w_{i} =$ Tempo di attesa del veicolo $i$ -esimo
$s_{i} =$ Tempo di servizio del veicolo del veicolo $i$ -esimo
$t_{i} =$ Intervallo tra l'arrivo del veicolo $i$ -esimo e del veicolo $i + 1$ -esimo
$w_{i + 1} =$ Tempo di attesa del veicolo $i + 1$ -esimo

Vale la relazione:

w_{i} + s_{i} > t_{i}

Pertanto, il tempo di attesa del veicolo $i + 1$ -esimo sarà dato da

w_{i + 1} = w_{i} + s_{i} - t_{i}

Simulazione con arrivi rari

Si può avere il caso in cui il secondo veicolo arriva quando il primo ha già terminato di usufruire del servizio. In questo caso l'andamento sarà descritto da questo diagramma:

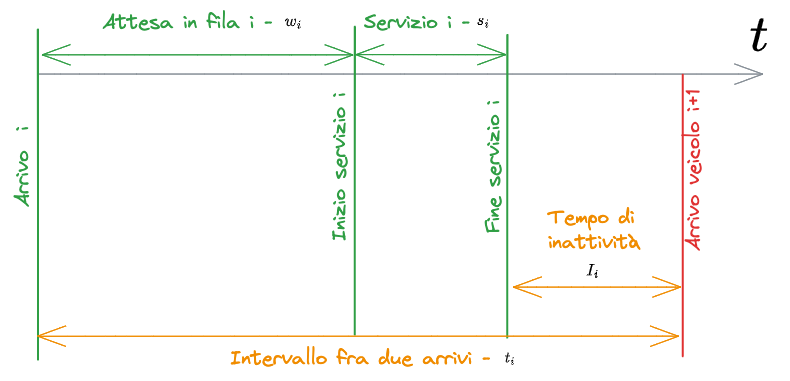
I simboli hanno lo stesso significato dei simboli in #Simulazione con arrivi frequenti. In più abbiamo:

$I_{i} =$ Tempo di inattività

In questo caso

w_{i} + s_{i} - t_{i} < 0

Per cui si avrà che il tempo di attesa del veicolo $i + 1$ -esimo sarà

w_{i + 1} = 0

[?] Ma $w_{i}$ non dovrebbe essere già uguale a zero? 📅 2023-10-27