04. Diagramma Elementare del Moto e Prestazioni del Veicolo Isolato

Altri libri di riferimento:

Ingegneria dei sistemi ferroviari - tecnologie metodi ed applicazioni, egaf
Orlandi Alessandro, Meccanica dei trasporti, ???
Leuzzi V., Fondamenti di trasporti - Appunti delle lezioni, facoltà di ingegneria di Roma
Scarponi P., Malavasi G., Fondamenti di trasporti - Applicazioni, Facoltà di Ingegneria di Roma

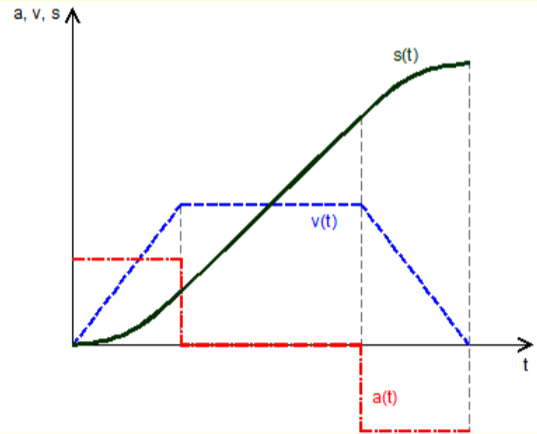
Diagramma Elementare del Moto

Forze sul veicolo in movimento

[Forze motrici]
[Forze Frenanti]
Resistenze ordinarie
Resistenze addizionali

Fasi di sosta

Si hanno quando

{\begin{cases} v = 0 \\ T - R = 0 \end{cases}

Fasi di movimento

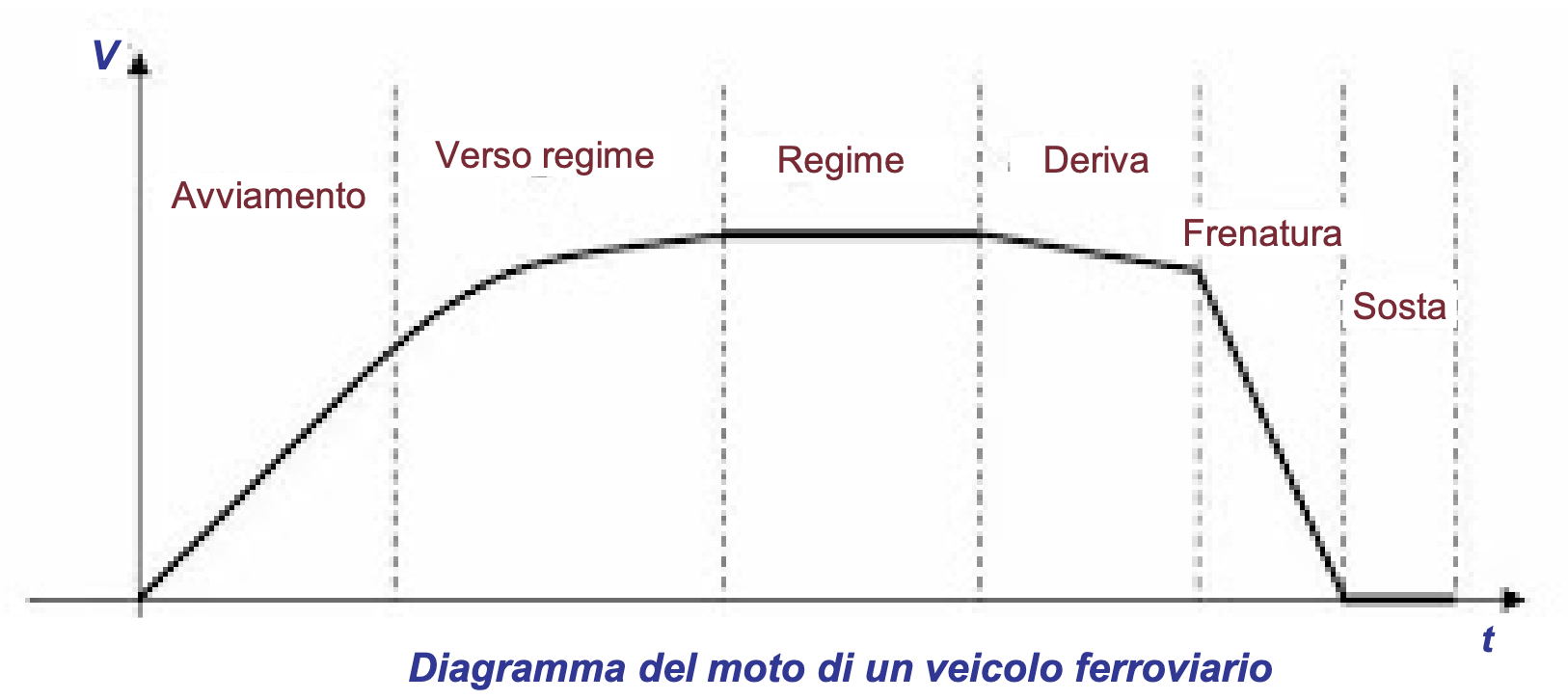
Si hanno quando

v \neq 0

Possono quindi verificarsi 4 casi:

{\begin{cases} T - R = 0 & v = c o s t \\ T - R < 0 & v ↘ \\ T - R > 0 & v ↗ \\ R > 0, T = 0 & D e r i v a \end{cases}

L'obiettivo è quello di risolvere l'equazione generale del moto:

T (v) - R (v) - R (s) = m_{e} a = m_{e} \frac{d v}{d t}

dove:

$v, a =$ Velocità e Accelerazione
$T (v) =$ Sforzo di trazione
$R (v) =$ Resistenze ordinarie (rotolamento e aerodinamica)
$R (s) =$ Resistenze addizionali (livelletta e curva)
$m_{e} =$ Massa equivalente (che tiene conto di tutte le inerzie)
$δ =$ Coefficiente di maggiorazione delle masse rotanti

m_{e} = m_{t a r a} (1 + δ) + m_{c a r i c o} \approx m (1 + δ)

Perché dalla slide 92 non c'è più $R (s)$ ma poi ricompare nella 96??
- Formule prese da fonti diverse con diverse approx. Dovrebbe esserci semrpe.
Nella slide 96, la trazione e la resistenza sono calcolate in $v_{m}$ ? Se no, come posso levarle dall'integrale?????????
- Esatto

Soluzione dell'equazione generale del moto

Per conoscere il moto di un veicolo dobbiamo risolvere l'equazione generale del moto. Per farlo la riscriviamo nella forma:

\frac{T (v) - R (v) - R (s)}{m_{e}} = \frac{d v}{d t}

che si può risolvere per separazione di variabili:

d t = m_{e} \frac{d v}{T (v) - R (v) - R (s)}

Questa andrebbe quindi integrata analiticamente restituendoci la funzione $v (t)$ .
In realtà è di nostro interesse conoscere la funzione $s (t)$ quindi, tenendo a mente la relazione

v d t = d s ⟹ d t = \frac{d s}{v}

possiamo riscrivere

d s = m_{e} \frac{v d v}{T (v) - R (v) - R (s)}

Poiché però le resistenze e la trazione dipendono dalla velocità e di solito non conosciamo analiticamente questa dipendenza, dovremo fare uso di alcuni metodi numerici per risolvere l'equazione non analiticamente ma sfruttando metodi di risoluzione alle differenze finite.
Potremmo principalmente adoperare 3 metodi distinti:

#Metodo $ Delta v$
#Metodo $ Delta s$
#Metodo $ Delta t$

È infatti noto il diagramma $T - R$ su $V$ :

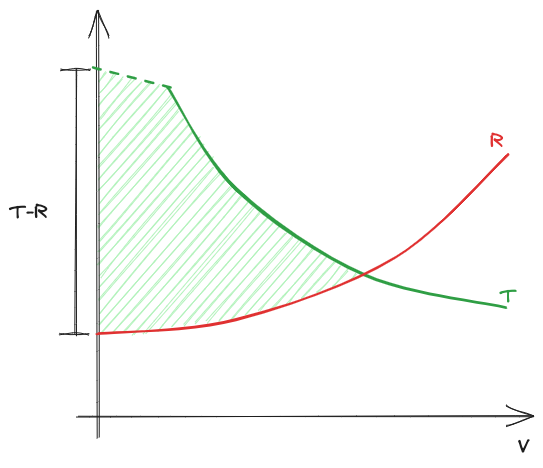
Metodo $Δ v$

Consiste nel partire da intervalli finiti di velocità.
Si scelgono $Δ v$ abbastanza piccoli in modo che tra $v_{i}$ e $v_{f}$ non vi siano variazioni troppo marcate della grandezza $T (v) - R (v)$ .
Si hanno quindi le seguenti grandezze:

{\begin{cases} v_{i} \\ v_{f} = v_{i} + Δ v \\ v_{m} = v_{i} + \frac{1}{2} Δ v \end{cases}

Possiamo quindi ricavare il valore medio dell'accelerazione nell'intervallo

\frac{Δ v}{Δ t} = a_{m} = \frac{T (v_{m}) - R (v_{m}) - R (s_{m})}{m (1 + δ)}

Una volta ricavata la $a_{m}$ si può facilmente trovare l'intervallo di tempo corrispondente:

Δ t = \frac{Δ v}{3.6 \cdot a_{m}}

dove il fattore $3.6$ è aggiunto per convertire da ore a secondi (Essendo la velocità espressa in $\frac{k m}{h}$ )
Si ricava quindi anche lo spazio percorso nell'intervallo di tempo considerato:

Δ s = \frac{v_{m} Δ t}{3.6}

attenzione

Facendo questa operazione si sta considerando la velocità costante e pari a $v_{m}$ in ogni intervallo.

Siccome ho già supposto che l'accelerazione sia costante quando ho calcolato l'intervallo di tempo, posso pensare di trovare l'intervallo spaziale in un modo alternativo per ridurre gli errori commessi.
A partire dall'equazione generale del moto posso scrivere
$\begin{aligned} \int Δ s & = \frac{m_{e}}{T (v_{m}) - R (v_{m}) - R (s_{m})} \int_{v_{i}}^{v_{f}} Δ v \\ Δ s & = \frac{m_{e}}{T (v_{m}) - R (v_{m}) - R (s_{m})} \frac{v_{f}^{2} - v_{i}^{2}}{2 \cdot {3.6}^{2}} \end{aligned}$

Il procedimento si ripete andando via via avanti nel moto. Nel farlo, dobbiamo confrontare i risultati con il percorso che si suppone noto. Se un intervallo finisse per scavallare punti di rilievo (come cambio di pendenze, curve...) occorrerebbe ridurre gli intervalli in modo da ovviare a questo problema.

Metodo $Δ s$

Per ovviare al fatto che nel #Metodo $ Delta v$ occorra ricalibrare gli intervalli in modo da evitare le variazioni di condizioni che si verificano lungo il tracciato, posso pensare di risolvere l'equazione generale del moto a partire proprio dai $Δ s$ .

{\begin{cases} s_{i} \\ s_{f} = s_{i} + Δ s \end{cases}

Comincio con il trovare l'accelerazione iniziale da:

a_{i} = \frac{T (v_{i}) - R (v_{i})}{m (1 + δ)}

È evidente che il metodo non è applicabile se parto con velocità iniziale nulla!!
otterrei infatti:

Δ t (1) = \frac{3.6 Δ s}{v_{i}}

che non posso calcolare se $v_{i} = 0$ .

04. Diagramma Elementare del Moto e Prestazioni del Veicolo Isolato

Diagramma Elementare del Moto

Fasi di sosta

Fasi di movimento

Soluzione dell'equazione generale del moto

Metodo $Δ v$

Metodo $Δ s$

Metodo $Δ t$

Rappresentazione del moto del veicolo isolato

Diagramma Elementare del Moto

Fasi di sosta

Fasi di movimento

Soluzione dell'equazione generale del moto

Metodo Δv

Metodo Δs

Metodo Δt

Rappresentazione del moto del veicolo isolato

Metodo $Δ v$

Metodo $Δ s$

Metodo $Δ t$