3. Sostentazione e Locomozione

La sostentazione è una delle quattro funzioni principali a cui devono assolvere i veicoli di trasporto
La funzione che permette al veicolo di rimanere sospeso sul mezzo che percorre.

Sostentazione

Una prima classificazione dei modi di trasporto si può effettuare sulla base della #Sostentazione:

• #Sostentazione terrestre
• #Sostentazione a vie d'acqua
• #Sostentazione aerea

Sostentazione terrestre

Che viaggia su terra.
Sfrutta la reazione del terreno.
Vale per

• Veicoli terrestri
• Aeromobili prima del decollo e dopo l'atterraggio

A sua volta si può essere:

• #Sostentazione a guida libera
• #Sostentazione a guida vincolata

Sostentazione a guida libera

Il #veicolo è libero di scegliere la propria traiettoria.

Sostentazione a guida vincolata

Il #veicolo è costretto nella sua traiettoria da una qualche guida.
Ne sono esempio le ferrovie, le funivie...

Sostentazione a vie d'acqua

A sua volta si divide in:

• #Sostentazione idrostatica
• #Sostentazione idrodinamica

Sostentazione idrostatica

Sfrutta il Principio di Archimede

Sostentazione idrodinamica

• Spinta per reazione di aria fredda con acqua o terreno (Hovercraft)

Sostentazione aerea

A sua volta si divide in:

• #Sostentazione aerostatica
• #Sostentazione aerodinamica

Sostentazione aerostatica

• Dirigibile
• Mongolfiera

Sostentazione aerodinamica

• Spinta con reazioni di aria calda o gas combusti
  • Con fluido ambiente (Esoreattori aeronautici: turbogetti, missili)
  • Senza fluido ambiente (Endoreattori: razzi)

Locomozione

Propulsione

Trazione

Sistemi di propulsione

Può essere:

• #Aderenza
• #Reazione

Aderenza

• Naturale: l'attrito che c'è naturalmente tra materiali
• Artificiale: Per mezzo di ruote dentate, cremagliere, o altri dispositivi...

Tra due corpi non in scorrimento tra loro.

C'è un coefficiente di aderenza tra la ruota e la strada/ferrovia.

Traino con la fune

<--#Aderenza

• Funicolari. Veicoli con ruote tirati con la fune
• Seggiovie e funivie

Cremagliera

<--#Aderenza

Ruota motrice

<--#Aderenza

Ruota trainata

<--#Aderenza

Reazione

<--#Aderenza

• Variazione della quantità di moto
  • Indiretta: del fluido ambiente (motore+elica)
  • Pura: della massa del sistema propulsore (razzo)
  • Diretta: di entrambi (reattore con un unico complesso motore propulsione)

Elica

<--#Aderenza

• Natanti
• Aeromobili

Esoreattore

<--#Aderenza

• Aeromobili
• Missili
• ...

Endoreattore

<--#Aderenza

• Razzi

Equazione generale del moto

La #Locomozione richiede che un motore fornisca energia per la traslazione
La forza di trazione $T$ che risulta applicata al mezzo deve essere in grado di vincere le resistenze al moto e di produrre accelerazione secondo l'equazione generale del moto.

• $T(v)=$ Forza di trazione, altrimenti definita come risultante delle forze attive
• $R_{\mathrm{t}\mathrm{o}\mathrm{t}}(v)=$ Somma delle resistenze al moto
• $m=$ Massa del veicolo che subisce l'azione delle forze attive e passive
• $\beta =$ Coefficiente di maggiorazione delle masse rotanti per tenere conto della necessità di accelerare masse rotanti e traslanti lungo traiettorie diverse da quelle del veicolo

Caratteristica meccanica di trazione

La funzione $T(v)$ è chiamata Caratteristica meccanica di trazione del mezzo e dipende dalla caratteristica meccanica del motore $C(n)$, dove $C$ è la coppia fornita dal motore all'albero e $n$ è il numero di giri dell'albero stesso.

Tornando all'equazione generale del moto:

Immaginiamo di saperla risolvere, dobbiamo trovare la forza necessaria a muovere il veicolo e trovare la caratteristica ???.

La caratteristica meccanica del veicolo è $T(v)$.

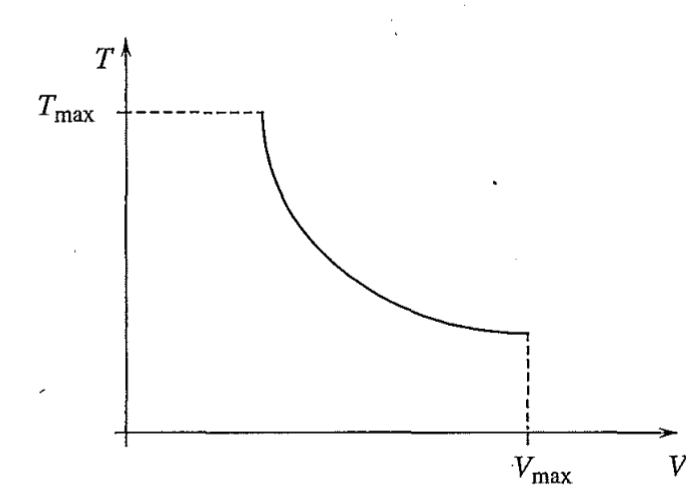
Ha come equazione: $T=\frac{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}{v}$
da cui

La potenza del motore invece:

Dove $n$ è il numero di giri

rendimento:

Può essere anche $\eta =0.97$.

Il motore può anche lavorare a potenza costante. Che è il caso ideale.
La Caratteristica meccanica del veicolo ideale permette di lavorare a potenza costante e alla potenza massima del motore per cui è stato progettato quel motore.

Si può ricavare a partire dalla caratteristica meccanica dei motori a bordo.

Il motore può erogare una certa coppia ($C_m$) in funzione del numero di giri. Da quella, si può risalire alla caratteristica meccanica del veicolo.
Per farlo dobbiamo conoscere il rapporto di trasmissione.

Nei veicolo stradali cambia cambiando la marcia.
Otteniamo quindi tante curve di $T(v)$ quante sono le marce del veicolo.

La caratteristica di trazione ideale è un'iperbole equilatera.
È limitata.

Per l'iperbole, se la trazione andasse a 0, la velocità andrebbe a infinito e viceversa.

• La forza massima di trazione a basse velocità è data dal limite di aderenza oppure dai limiti di confort
• Ad alta velocità, il limite è imposto dalle prestazioni del mezzo di trazione (velocità massima di rotazione del collettore nei motori a corrente continua) o delle condizioni di sicurezza (caratteristiche del binario e del tracciato plano-altimetrico o del sistema di segnalamento per il trasporto ferroviario)

La caratteristica di trazione ideale è anche stabile. Non è detto il viceversa.

Le resistenze le possiamo quasi sempre schematizzare con un andamento parabolico.
La resistenza al moto non va mai a 0, neanche a velocità nulla. C'è sempre la forza di primo distacco.

Resistenze al moto

Ci sono:

Fattori causali

I fattori che causano #Resistenze al moto sono:

• Natura del mezzo ambiente
• Modalità di sostentazione e locomozione
• Caratteristiche del moto (traiettoria, velocità, accelerazione)
• Massa del veicolo

Resistenze specifiche

Nel mondo dei trasporti si tende a considerare le resistenze per unità di peso:

• $r=$ Resistenza specifica ($\frac{N}{kN}=\frac{kg}{t}$ con chilogrammo e tonnellata peso) - $1kg=10N=10k{g}_p$
• $R=$ Resistenza totale

Resistenze ordinarie e addizionali

Si ha che le resistenze possono essere:

• #Resistenze ordinarie
• #Resistenze Addizionali

Resistenze ordinarie

Le registriamo nel:

• Moto piano
• Moto Rettilineo
• Moto uniforme

Le fonti di #Resistenze al moto ordinarie sono principalmente:

• Ruota - Terreno per i veicoli stradali
• Assi - Telaio per i veicoli ferroviari

Tra le resistenze ordinarie, troviamo:

• #Resistenza al rotolamento
• #Rotolamento perno-cuscinetto
• #Resistenza aerodinamica

Resistenza al rotolamento

Una Resistenza ordinaria

Immaginiamo di avere una ruota ferma. Questa, per via del carico che porta (peso) si deformerà in corrispondenza della superficie di contatto. Il peso sarà quindi distribuito su una certa superficie secondo un campo di pressioni che si dimostra essere parabolico.

Immaginiamo ora che la ruota si muova a velocità costante verso destra, mossa da una forza trainante $T$ applicata nel suo asse di rotazione. L'esperienza ci dice che senza la forza, una volta in movimento la ruota tenderà a fermarsi. Deve esserci una qualche forma di attrito di rotolamento. Al punto di contatto troveremo due reazioni del terreno, una diretta verso l'alto, l'altra verso sinistra. Le reazioni le consideriamo applicate a una distanza $x$ dalla proiezione dell'asse di rotazione

Andando a scrivere le equazioni cardinali per il sistema sopra, usando come polo dei momenti il centro di rotazione, avremo:

Dalla legge dell'attrito abbiamo che

e quindi

con $R$ dato, una volta risolto il sistema, da

In definitiva possiamo esprimere il coefficiente di attrito come:

Rotolamento ruota-strada

Nel campo stradale, la #Resistenza al rotolamento dipende da

• Pressione di gonfiaggio
• Flessibilità della carcassa
• Attrito generato nell'area di impronta
• Attrito viscoso tra pneumatico e filetti fluidi dell'aria

La determinazione delle resistenze è effettuata per via sperimentale:

• In laboratorio (su tamburo)
• Su strada

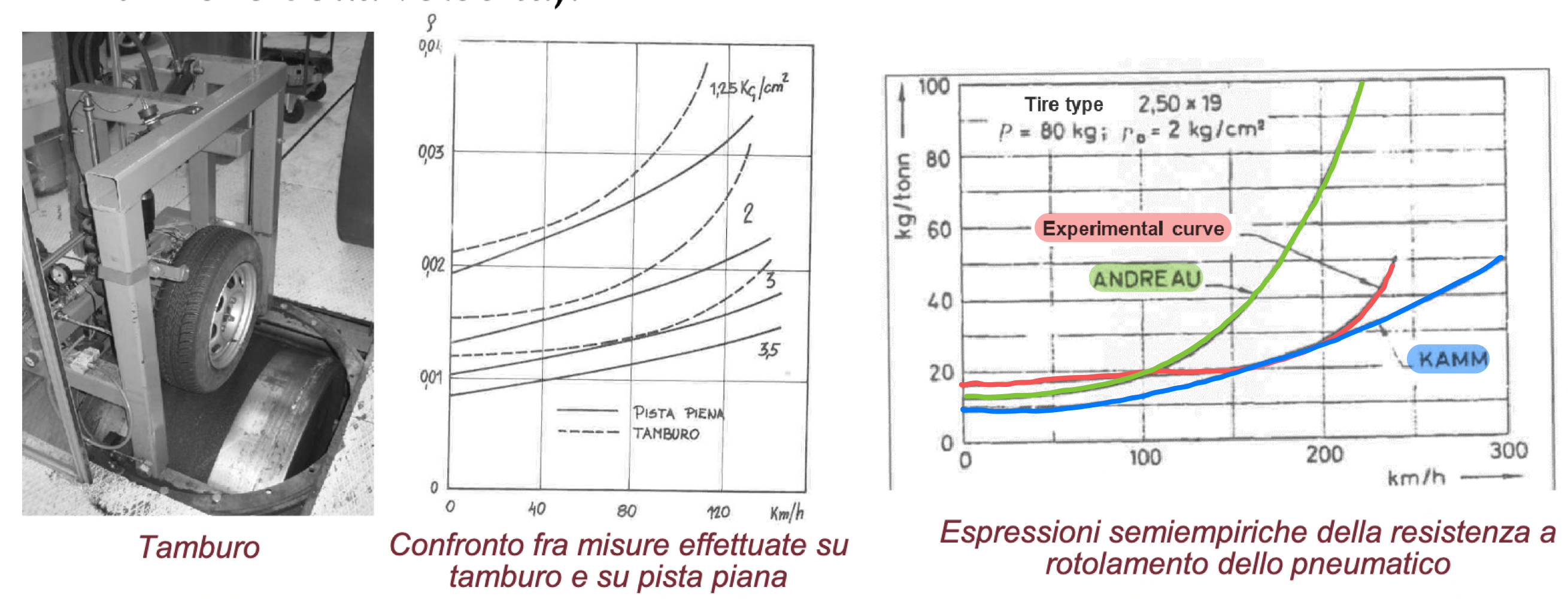
Come si vede nel grafico a dx, modelli diversi forniscono andamenti diversi delle resistenze in funzione della velocità. In rosso si vede il risultato sperimentale.

Rotolamento perno-cuscinetto

Ci sono 2 tipi di cuscinetti

• #Cuscinetto a Strisciamento
• #Cuscinetto a rotolamento

Cuscinetto a Strisciamento

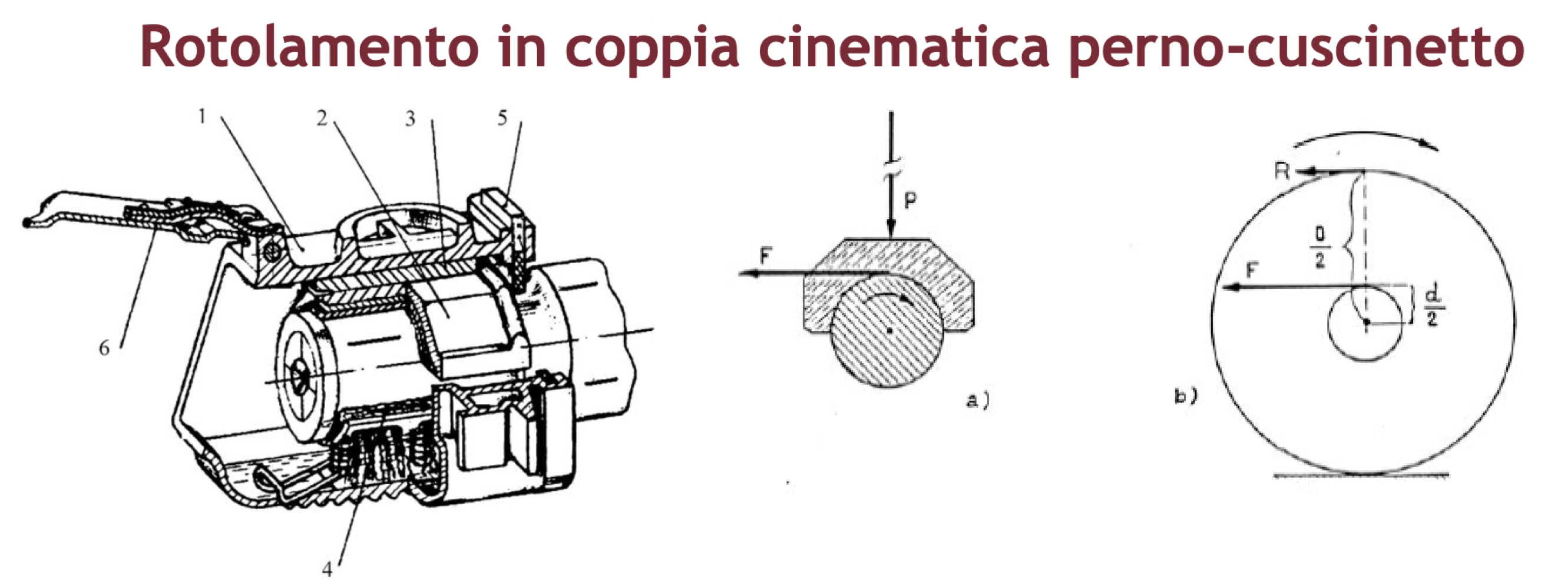
Una volta veniva chiamato bronzina (perché realizzato in una lega a base di bronzo).
Le due parti sono in contatto tra loro e lo scorrimento è assicurato da un'opportuna lubrificazione.

La forza di trazione deve vincere la coppia resistente provocata dall'attrito tra le parti del cuscinetto

Cuscinetto a rotolamento

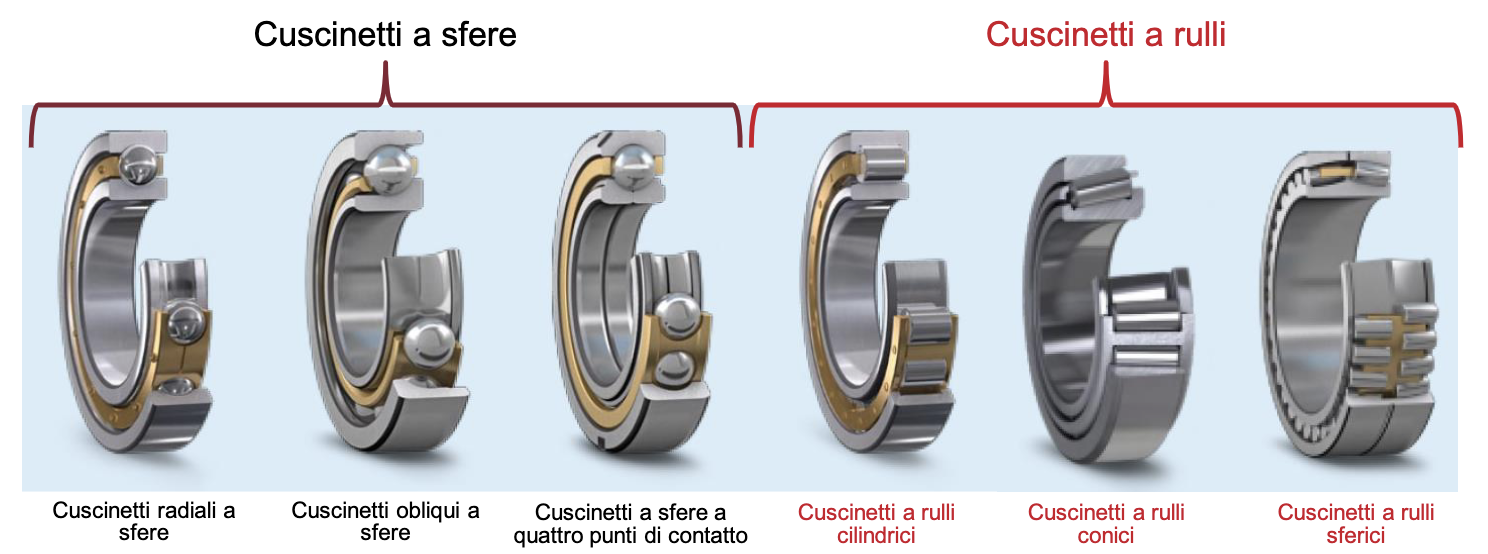
Il contatto è rotolante invece che strisciante. Il rotolamento può essere assicurato da:

• Sfere
• Rulli
  • cilindrici
  • Conici
  • Sferici
    La resistenza è leggermente crescente con la velocità

Resistenza aerodinamica

È generata da

• Attrito
• Salto di pressioni
  ...tra veicolo e "tubo" d'aria che lo investe.

L'unico modo che abbiamo per eliminare del tutto la resistenza aerodinamica è quella di porre il veicolo in un tunnel sottovuoto.

Immaginiamo di avere una portata costante d'aria:

dove:

• $\rho =$ Densità dell'aria
• $S=$ Superficie
• $V=$ Velocità dell'aria

Dovendo $Q$ rimanere costante, è evidente che al diminuire della sezione disponibile al fluido, la velocità del flusso aumenta.

Nel caso ideale, quando un flusso attraversa un veicolo, arriva con velocità $V_0$, viaggerà con velocità $V_1>V_0$ lungo il veicolo (per via della sezione minore) e uscirà nuovamente a velocità $V_0$.

In realtà però interviene anche il Principio di Bernoulli, per cui l'energia totale dell'aria:

dove $P$ è la Pressione
Se $V_1>V_0$, se non ci sono dissipazioni di energia, $P_1<P_0$.

Nella realtà l'energia viene dissipata. Quindi all'uscita si ha che $V_2<V_0$ e $P_2<P_1<P_0$.

Si ha quindi una resistenza che si oppone al moto del veicolo. In corrispondenza del punto di uscita si genera un moto turbolento che fa si che ci sia un calo di pressione: ne corrisponde un elevato Numero di Reynolds, il che significa grande resistenza al moto.

La resistenza sarà data da:

dove:

• $C_r=$ Coefficiente di resistenza aerodinamica
• $\rho =$ Densità dell'aria
• $S=$ Sezione
• $V=$ Velocità del fluido

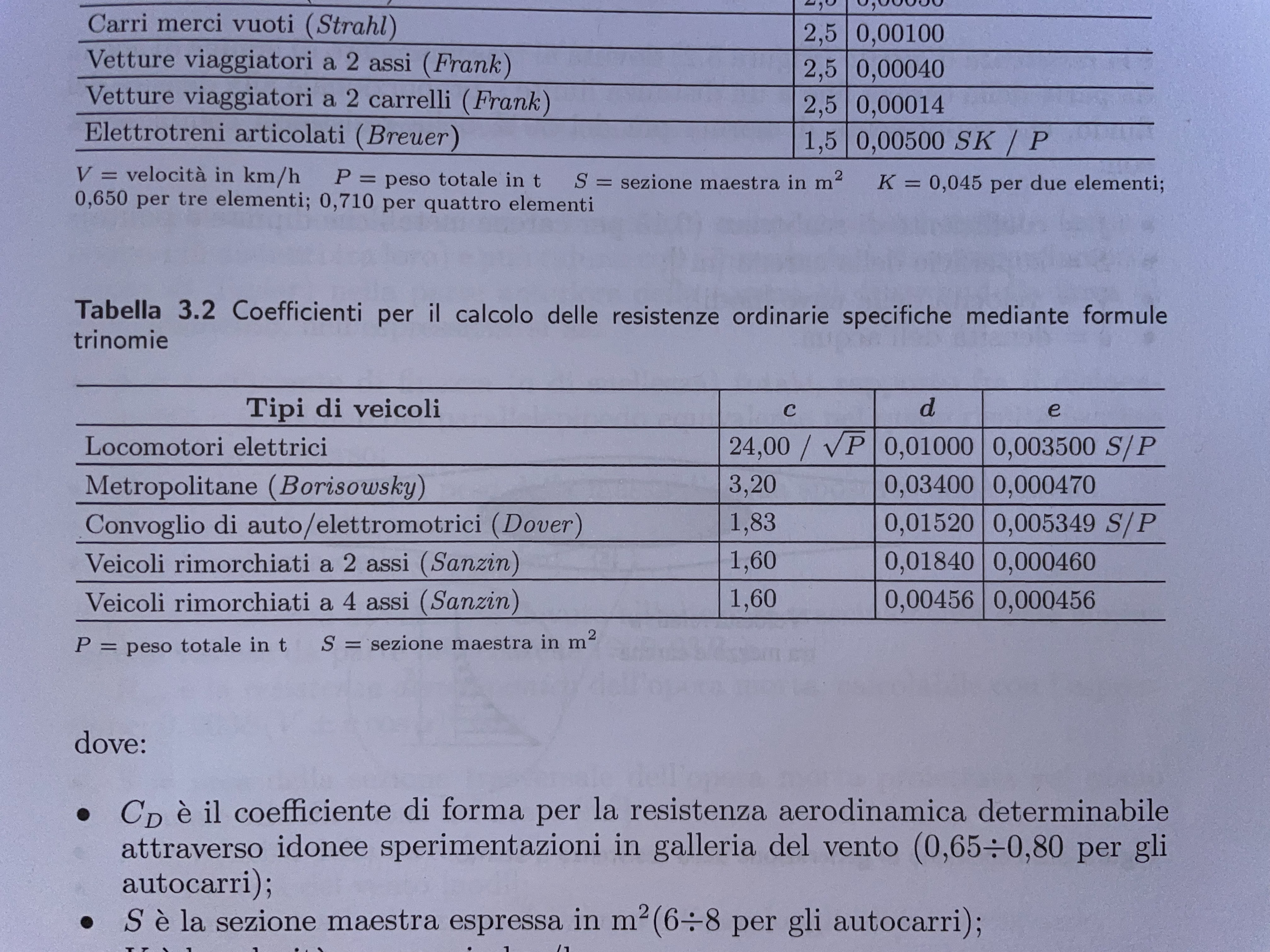
Formule binomie e trinomie

Visto i numerosi fattori che intervengono nel calcolo della resistenza, si segue un approccio sperimentale.
Sperimentalmente si trovano delle formule, dette formule binomie e formule trinomie che quantificano la resistenza totale che agisce su un veicolo.

dove

• $r=$ Resistenza specifica
• $v=$ Velocità del veicolo in $\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}$
• $a,b,c,d,e=$ coefficienti determinati sperimentalmente per vari tipi di veicolo

La differenza tra formula binomia o trinomia sta nei tipi di resistenze che intervengono.

La resistenza al rotolamento dipende dalla velocità. A basse velocità la posso trascurare e uso quindi la formula binomia. A velocità più elevate sono costretto a tenerne conto e applico le formule trinomie.

Resistenze Addizionali

• Altre condizioni
  • Moto accelerato
  • Curva
  • Salita
  • Galleria
  • ...

Resistenza dovuta alla livelletta (pendenza)

Quando un veicolo cerca di risalire un pendio si ottiene una resistenza al moto addizionale

dove $\alpha$ è l'angolo del pendio e nei conti si approssima $\sin \alpha \approx \tan \alpha$.

Resistenze specifiche per tipo di veicolo

Resistenze al moto per Natanti

Il compendio generale delle resistenze per natanti ci dà la seguente formula:

dove:

• $R_a=$ #Resistenza di attrito tra opera viva e acqua (la parte sommersa)
• $R_v\approx 0.06R_a=$ Resistenza dovuta ai Vortici che si formano per depressioni a poppa
• $R_o=$ Resistenza dovuta alla #Generazione di onde a prua e poppa
• $R_{\mathrm{v}\mathrm{i}\mathrm{s}}\approx 0.03R_o=$ Resistenza dovuta al trascinamento di lamine viscose
• $R_{\mathrm{a}\mathrm{e}\mathrm{r}}=$ Resistenza dovuta all'attrito tra opera morta e aria

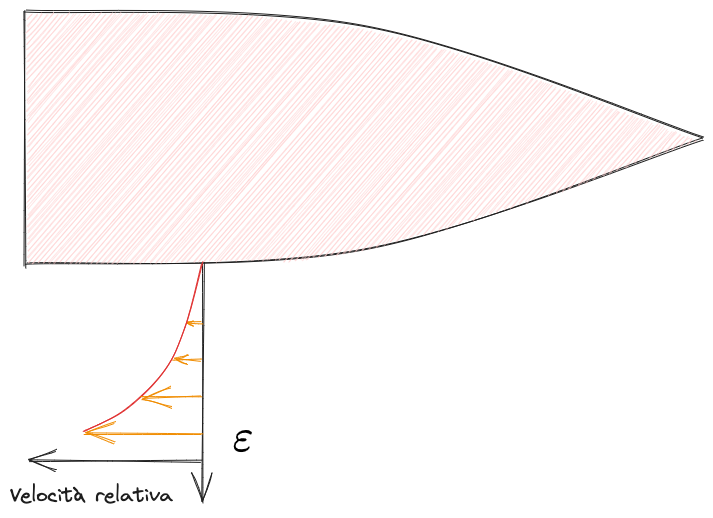
Resistenza di attrito tra opera viva e acqua

dove:

• $f=$ Coefficiente di scabrezza ($\approx 0.15$ per carene metalliche nuove)
• $S=$ Superficie della carena in ${\mathrm{m}}^2$
• $V=$ Velocità della nave in $\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{i}$
• $\delta =$ Densità dell'acqua

È la resistenza di attrito dovuta al trascinamento di lamine di acqua da parte della carena fino a una distanza limite $\epsilon$ proporzionale alla densità del fluido, che rappresenta di norma più del $50\mathrm{\%}$ della resistenza complessiva.

Generazione di onde a prua e poppa

dove:

• $D=$ Dislocamento: la massa d'acqua spostata dalla carena in tonnellate
• $\delta =$ Coefficiente di finezza (snellezza): il rapporto tra il dislocamento e il volume del parallelepipedo equivalente nel quale risulta iscritta l'opera viva
• $V=$ Velocità della nave in nodi
• $L=$ Lunghezza della carena in $\mathrm{m}$

Viene ridotta con l'adozione del Bulbo di Taylor

Resistenza aerodinamica

dove:

• $S=$ Area proiezione ortogonale alla direzione del moto della sezione trasversale dell'opera morta
• $V=$ Velocità della nave in nodi
• $v=$ Velocità del vento in nodi
• $\alpha =$ Angolo tra la direzione del vento e asse longitudinale della nave

In assenza di vento si considera $R_{\mathrm{a}\mathrm{e}\mathrm{r}}=0.02R_{\mathrm{t}\mathrm{o}\mathrm{t}}$

Resistenze al moto per aeromobili

Le resistenze di cui tenere conto negli aeromobili sono dovuta al variare:

• della viscosità e della densità dell'aria
• della forma e dell'assetto dell'aeromobile
• del carico Q ovvero del carico alare $q={\displaystyle \frac{Q}{S}}$
• della velocità del vento relativo $V$

Nomenclatura aeromobili

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗