10. Processi Biologici
10. Processi Biologici
I processi biologici consistono nel replicare i processi biologici naturali all'interno dell'impianto di trattamento per depurare i reflui.
Li troviamo di solito a valle dei trattamenti primari.
I processi biologici possono essere:
- Anaerobici
- Anossici
- Aerobici
Inoltre, possono essere:
- A biomassa sospesa - ci sono microrganismi sospesi nel liquido nella forma di fiocchi
- A biomassa adesa - i microrganismi si accumulano aderendo alla materia
- Supporto fisso
- Supporto Mobile
Il vantaggio dei PB è quella di favorire la trasformazione del substrato organico in materia cellulare. La materia cellulare può essere più facilmente separata dalla fase liquida attraverso processi di 6. Sedimentazione.
Cerco di favorire nel reattore le reazioni che ci fanno comodo. Dobbiamo promuovere lo sviluppo di certe tipologie di biomassa.
Cercheremo di fare in modo che la biomassa cresca su un supporto.
Parliamo di sostanze tipo Sostanze Organiche Biodegradabili (SOB).
Serve un reattore dove far crescere Biomassa che degradi la SOB in condizioni aerobiche.
Processo biologico in un reattore di Batch
La cinetica biologica viene tipicamente studiata seguendo la crescita dei microrganismi in coltura pura.
Si ipotizza che una certa quantità di microrganismi venca introdotta a un certo istante in un reattore batch.
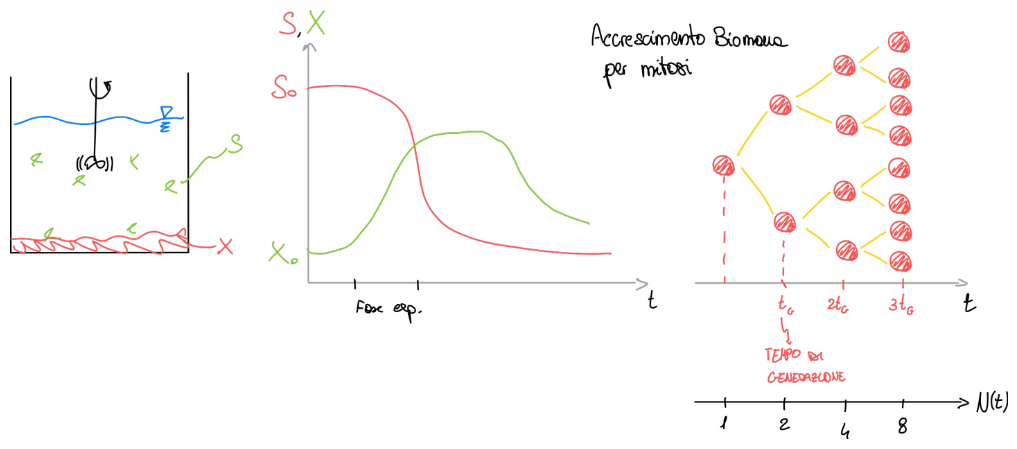
Alla fine della fase di acclimatazione, la biomassa cresce in maniera esponenziale per mitosi. Nella fase di crescita esponenziale, il substrato non è limitante alla crescita --> la biomassa cresce alla velocità max (liberamente).
L'incremento della popolazione microbica seguirà una progressione geometrica.
Il numero di microrganismi all'istante
dove:
Numero di microrganismi all'istante 0 Tempo di generazione: il tempo impiegato per la mitosi
Passando ai logaritmi posso scrivere:
dove definisco il #Tasso massimo di crescita della biomassa:
Quando la quantità di substrato è limitante per la crescita della biomassa si ha la fase di respirazione endogena. In tali condizioni, il tasso di crescita è espresso dall'#Equazione di Monod.
Si definiscono ora alcune grandezze utili a caratterizzare le velocità di crescita di substrato e biomassa:
- #Grandezze del substrato
- #Grandezze della Biomassa
Grandezze del substrato
Si avranno:
- #Velocità di utilizzazione del Substrato
- #Tasso di utilizzazione del Substrato
Si definisce inoltre una relazione che metta in relazione il #Tasso di crescita lorda della Biomassa con la concentrazione di substrato: l'#Equazione di Monod:
Equazione di Monod
L'equazione di Monod mette in relazione il #Tasso di crescita lorda della Biomassa con la concentrazione di substrato
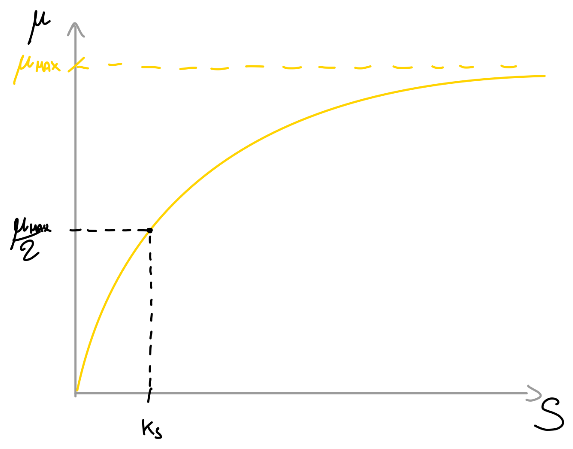
Velocità di utilizzazione del Substrato
In quanto il substrato diminuisce, per avere velocità positiva si inserisce un segno
Tasso di utilizzazione del Substrato
Il tasso di utilizzazione, è una velocità specifica, normalizzata in termini di biomassa:
Grandezze della Biomassa
- #Velocità di crescita lorda della Biomassa
- #Velocità di respirazione endogena della Biomassa
- #Velocità di crescita lorda della Biomassa
In generale non si fa riferimento alle velocità ma al loro valore specifico (tasso) rispetto alla concentrazione della biomassa
- #Tasso di crescita lorda della Biomassa
- #Tasso di respirazione endogena della Biomassa
- #Tasso di crescita netta della Biomassa
Velocità di crescita lorda della Biomassa
g = gross
Tasso di crescita lorda della Biomassa
Velocità di respirazione endogena della Biomassa
dove "d" sta per decadimento
Tasso di respirazione endogena della Biomassa
Velocità di crescita netta della Biomassa
Tasso di crescita netta della Biomassa
Tasso di rendimento di crescita
Non tutto il substrato che viene consumato diventa biomassa, infatti:
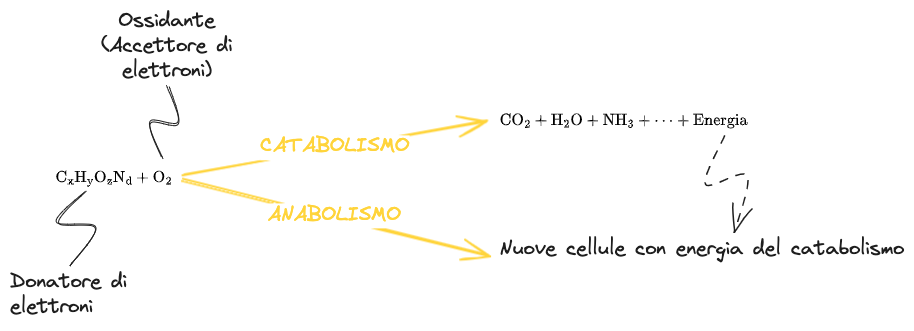
Della quantità complessiva di substrato consumato nelle reazioni biologiche,
- una parte viene trasformata in prodotti finali dando luogo alla produzione di energia
- la parte restante è usata per la costruzione di nuovo materiale cellulare
Si definisce pertanto un Tasso di rendimento di crescita:
Il Tasso di rendimento di crescita è il rapporto tra quanta biomassa nasce rispetto a quanto substrato viene consumato:
che di solito assume valori
Il vantaggio che si ottiene coi processi biologici è di convertire il substrato (disciolto) in biomassa, la quale è più facile da rimuovere.
Reattore a fanghi attivati
Un reattore a fanghi attivati è un reattore all'interno del quale la rimozione della sostanza organica viene realizzata sfruttando opportune reazioni biochimiche di degradazione.
- Attivati: perché siamo noi a introdurre i microrganismi

Nel nostro sistema si avrà pertanto crescita di biomassa la quale crescerà proprio nutrendosi del substrato. La biomassa poi è più facile da rimuovere per sedimentazione rispetto al substrato.
Un sistema a fanghi attivati sarà pertanto costituito da:
- Un reattore biologico (CFSTR) in cui la biomassa cresce consumando substrato
- Un sedimentatore secondario in cui la biomassa viene fatta sedimentare in un fango di scarto
- Il liquido depurato in uscita dal sistema
Un sistema a fanghi attivati può poi avere o meno ricircolo del fango in uscita dal sedimentatore secondario. Di seguito sono analizzati entrambi i casi:
- #Sistema a fanghi attivati - senza ricircolo
- #Sistema a fanghi attivati - con ricircolo e spurgo dalla linea di ricircolo
Sistema a fanghi attivati - senza ricircolo
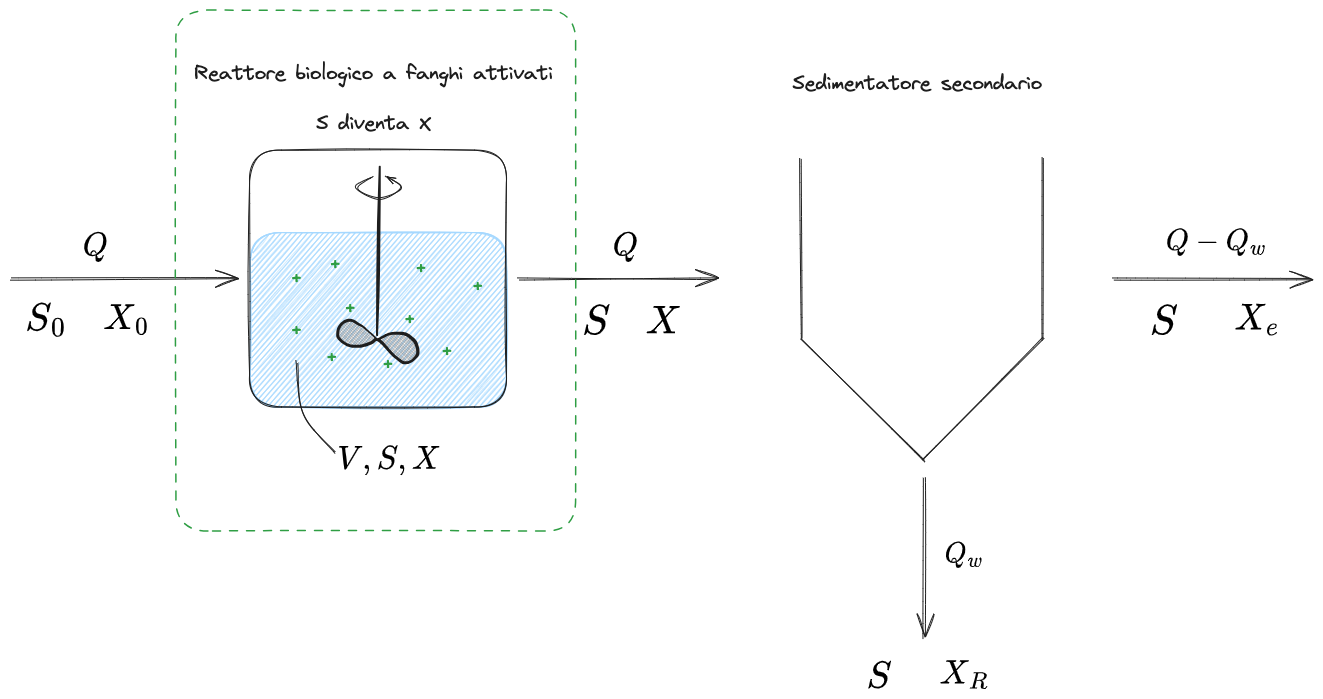
In ingresso si avranno concentrazioni di Substrato ed eventuale Biomassa (
In uscita dal CFSTR, così come al suo interno, si avranno invece concentrazioni minori di Substrato,
Nel sedimentatore secondario, la biomassa viene fatta sedimentare ed espulsa (portata
Per quanto riguarda il substrato invece, si suppone che nel sedimentatore la sua concentrazione non vari. Essendo poi questo disciolto in acqua, avrà la stessa concentrazione nel fango e nell'effluente, sempre pari a
Riassumendo:
Si mostrano sotto le unità di misura con cui vengono misurate le concentrazioni di substrato e biomassa:
Equazioni di progetto - senza ricircolo
Per trovare le equazioni di progetto per i #Sistema a fanghi attivati - senza ricircolo occorre prima di tutto fare i bilanci di materia per substrato e Biomassa. In entrambi i casi si eseguirà il bilancio supponendo le condizioni stazionarie.
Bilanci per Substrato e Biomassa
Bilancio del Substrato - senza ricircolo
Ricordando come si esegue il bilancio di materia per un reattore, avremo:
dove:
#Velocità di utilizzazione del Substrato - Accumulo supposto uguale a zero per via delle condizioni stazionarie
Isolando per
dove il rapporto
Ricordando infine la definizione di #Tasso di utilizzazione del Substrato, possiamo riscrivere anche questo come:
Bilancio della Biomassa - senza ricircolo
Ricordando come si esegue il bilancio di materia per un reattore, avremo:
dove:
Portata in massa in ingresso Portata in massa in uscita #Velocità di crescita netta della Biomassa - Accumulo supposto uguale a zero per via delle condizioni stazionarie
Si ricorda inoltre quanto detto nell'introduzione ai #Sistema a fanghi attivati - senza ricircolo:
Per cui il bilancio fornisce, trascurando il contributo dato dalla biomassa in ingresso, la seguente equazione per la #Velocità di crescita netta della Biomassa:
dove il rapporto
Ricordando infine la definizione di #Tasso di crescita netta della Biomassa, possiamo riscrivere anche questo come:
Equazione di progetto per il substrato - senza ricircolo
Si è quindi trovato, rispettivamente nei #Bilancio del Substrato - senza ricircolo e #Bilancio della Biomassa - senza ricircolo che:
Ricordando inoltre l'#Equazione di Monod:
possiamo scrivere:
Risolvendo a questo punto per
Equazione di progetto per la biomassa - senza ricircolo
Ricordando il #Tasso di rendimento di crescita, nonché quanto trovato nel #Bilancio del Substrato - senza ricircolo e nel #Bilancio della Biomassa - senza ricircolo, rispettivamnte
scriveremo:
a questo punto, risolvendo per
Sistema a fanghi attivati - con ricircolo e spurgo dalla linea di ricircolo
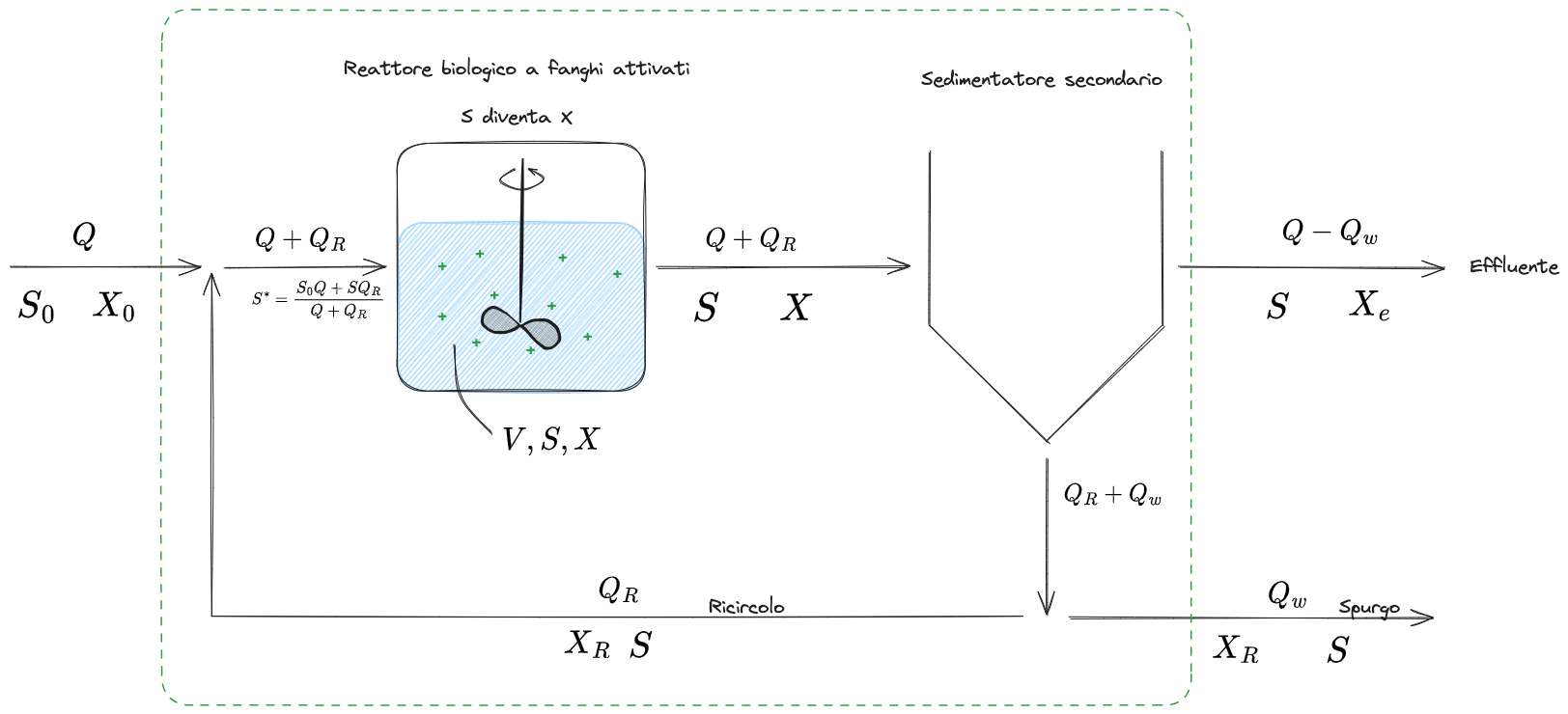
Definisco il #Tempo di residenza cellulare
Tempo di residenza cellulare
Il tempo di residenza cellulare (o anche età del fango) indica quanto tempo la Biomassa risiede nel sistema.
con
è un valore medio: è una media statistica ha significato solo in condizioni di stato stazionario - Rappresenta quanto tempo ci mettiamo a rinnovare tutta la biomassa nel reattore.
- [?] Perché
rappresenta quanto tempo ci mettiamo a rinnovare tutta la biomassa nel reattore?
Equazioni di progetto - con ricircolo
Si trovano le equazioni di progetto nel caso di #Sistema a fanghi attivati - con ricircolo:
Bilanci per substrato e biomassa - con ricircolo
Bilancio del Substrato - con ricircolo
Ricordando come si esegue il bilancio di materia per un reattore, avremo:
dove:
Portata in massa in ingresso Portata in massa in uscita #Velocità di utilizzazione del Substrato - Accumulo supposto uguale a zero per via delle condizioni stazionarie
Facendo le dovute semplificazioni e risolvendo per la #Velocità di utilizzazione del Substrato si ottiene:
Si noti che l'espressione è uguale a quella ottenuta per il sistema senza ricircolo.
Bilancio della Biomassa - con ricircolo
Ricordando come si esegue il bilancio di materia per un reattore, avremo:
dove:
Portata in massa in ingresso Portata in massa in uscita #Velocità di crescita netta della Biomassa - Accumulo supposto uguale a zero per via delle condizioni stazionarie
Inoltre, si trascura la componente in ingresso
Risolvendo per la #Velocità di crescita netta della Biomassa:
passando al #Tasso di crescita netta della Biomassa si ottiene:
dove si è usata la definizione di #Tempo di residenza cellulare.
Equazione di progetto per il Substrato - con ricircolo
Si omettono i passaggi che sono del tutto analoghi a quelli fatti per ricavare l'#Equazione di progetto per il substrato - senza ricircolo.
Si ottiene così
Equazione di progetto per la Biomassa - con ricircolo
Si omettono i passaggi che sono del tutto analoghi a quelli fatti per ricavare l'#Equazione di progetto per la biomassa - senza ricircolo.
Si ottiene così
I parametri cinetici li diamo per costanti.
Analisi delle equazioni di progetto - con ricircolo
Si rappresentano gli andamenti delle Equazioni di progetto, sia per il Substrato
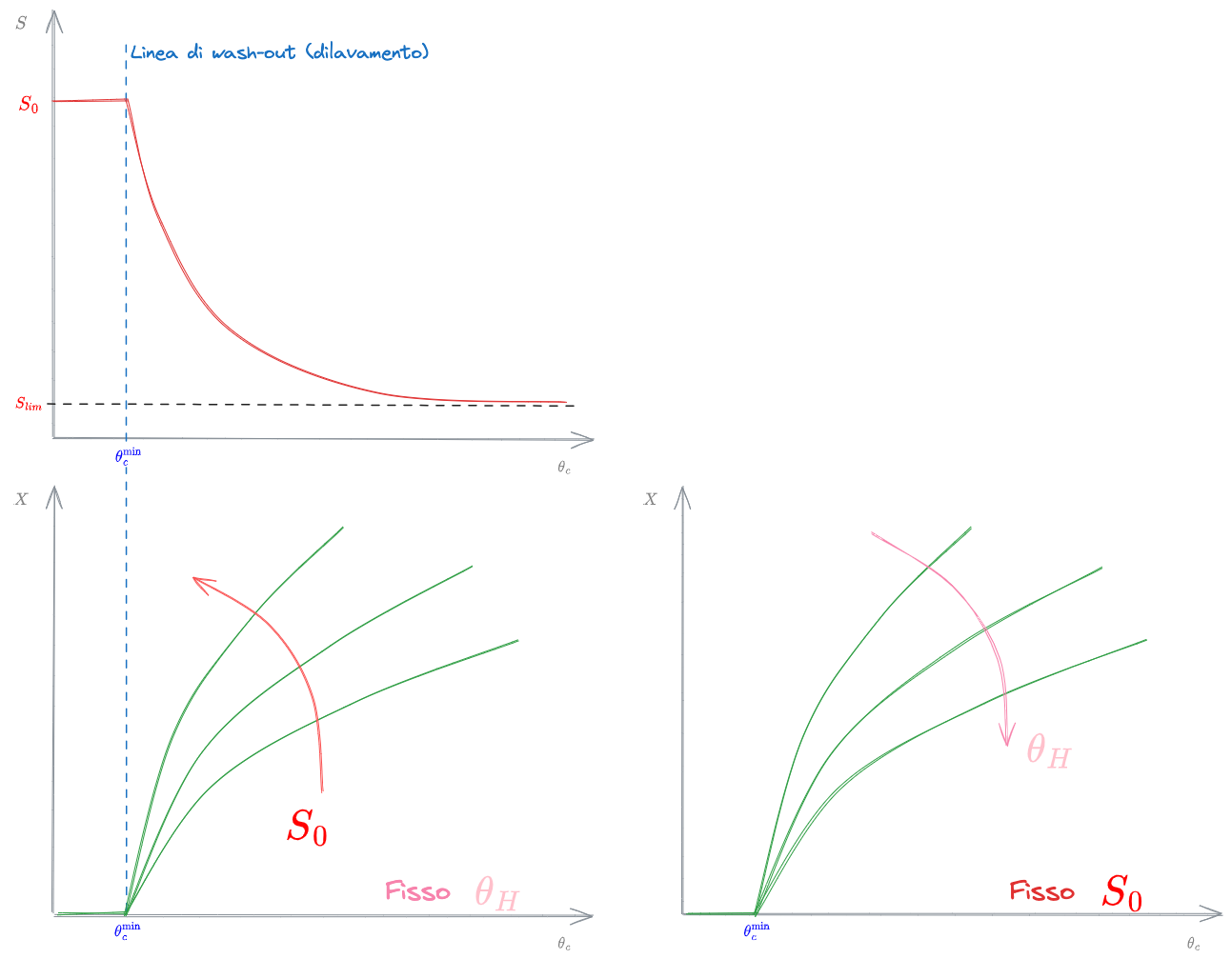
È sbagliato dire prima o dopo in senso temporale.
I grafici raffigurano per ogni valore di
Curva del substrato
CURVA del SUBSTRATO:
Si noti che la curva del Substrato è tagliata al valore
A valore bassi di
Curva della Biomassa
CURVA della BIOMASSA:
Per quanto riguarda la biomassa non è possibile costruire un'unica curva, in quanto l'andamento dipenderà, oltre che da
Si noti prima di tutto che, per valori di
- [?] Perché per valori bassi di
si ha concentrazione nulla di biomassa?
Inoltre, fissato un certo valore di
Infatti, dall'#Equazione di progetto per la biomassa - con ricircolo, si ha che
È evidente che, fissato
Questo si verifica perché, essendo
Se
Valore limite del Substrato
VALORE LIMITE del SUBSTRATO:
Si osservi inoltre che
- [?] Perché S non va a 0 per
che va a infinito in termini intuitivi? - [?] "
non va a 0 perché serve un minimo di substrato per avere una certa quantità di biomassa". Cosa vuol dire questa frase?
ile contengono i parametri cinetici: e (e ). Stiamo considerando che dentro c'è della biomassa che reagisce per consumare il substrato.
Abbiamo detto che
- Non c'è rimozione di substrato
- Non c'è biomassa nel sistema
Si osservi cosa avevamo trovato nel #Equazione di progetto per la biomassa - con ricircolo:
Si vede che, più la biomassa risiede all'interno del #Sistema a fanghi attivati - con ricircolo, più cresce lentamente, essendo
Inoltre ricordando l'#Equazione di Monod:
Ci mettiamo ora nella condizione in cui
Inoltre, supponendo che sia
Punto di washout
PERCHÉ ESISTE
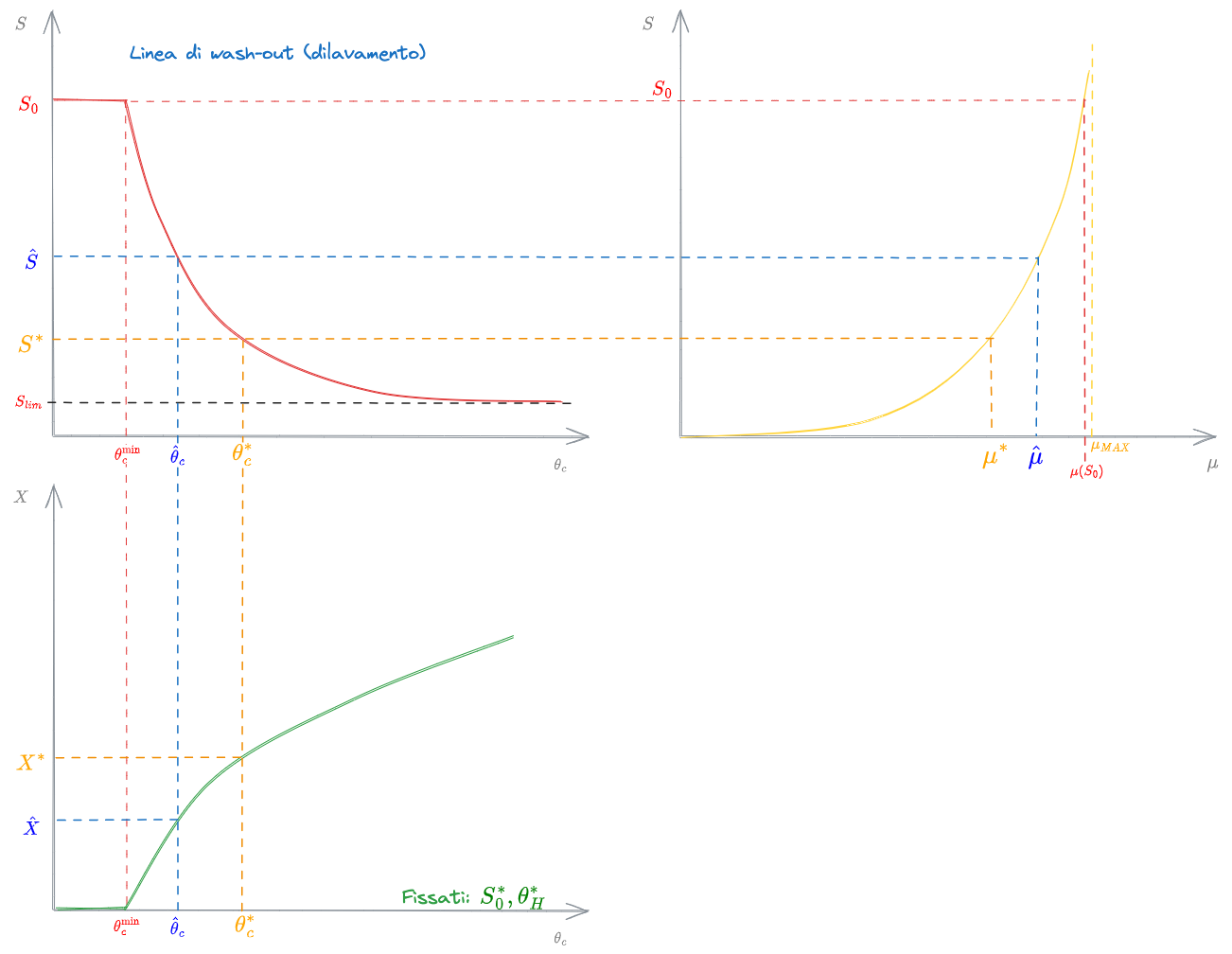
Dobbiamo garantire che la Biomassa rimanga nel reattore almeno
Ricordo la definizione di #Tempo di residenza cellulare:
Per capire il perché sotto
Prendo
Prendo un certo valore di
SI può anche calcolare il #Tasso di crescita netta della Biomassa,
Inoltre, si è trovato che c'è proporzionalità inversa tra il tempo di residenza cellulare e il tasso di crescita netta della biomassa:
Siamo noi a indurre una certa quantità di biomassa, lavorando a un determinato valore di
Prendo
Si considera ora un valore di
Ora, i microrganismi hanno meno tempo per degradare il substrato.
E quindi sarà necessaria meno biomassa per degradare meno substrato.
Quindi, per
Ossia, per valori di concentrazione di biomassa minore, e concentrazione di substrato maggiore, si avrà un tasso di crescita di microrganismi maggiore.
Infine, se prendo come
Prendendo
A questo punto, a valori di
Ad esempio, è come se, quando nel reattore nascono 20 microrganismi, cerco di spurgarne 25. In una prima fase di transitorio questo sarebbe anche possibile, ma è chiaro che in condizioni stazionarie la cosa non potrebbe funzionare. Arriverei a voler rimuovere un numero di organismi maggiore di quelli che effettivamente ho
Per valori di
Per quanto appena detto, il punto di
Obbligatorietà dello spurgo
Se non ci fosse spurgo sarebbe meglio. Infatti nella realtà lo spurgo è un flusso contenente circa la metà del substrato rimasto.
È impossibile però non avere spurgo.
Infatti, al fine di mantenere la condizione stazionaria, se ci fosse crescita di biomassa, dovrei comunque aumentare lo spurgo.
La quantità di Biomassa (
Al crescere di tanta biomassa, bisogna spurgare tanto, provocando un abbassamento del tempo di residenza cellulare.
Produzione di Biomassa
È legata al
La Produzione di biomassa è la crescita della Biomassa nell'unità di tempo. Rappresenta la nuova biomassa che viene prodotta dal sistema. Tenendo sempre a mente di voler mantenere le condizioni di stato stazionario, corrisponderà anche alla biomassa che viene espulsa nello spurgo nell'unità di tempo ([[#Obbligatorietà dello spurgo]]).
Ammesso di trovarci in condizioni stazionarie:
Ne risulta, direttamente dalla definizione, che il #Tempo di residenza cellulare è:
E quindi, ricordando l'#Equazione di progetto per la biomassa - con ricircolo:
Ricordando che
mentre la quantità
Rendimento effettivo di crescita della biomassa
Il rendimento effettivo di crescita della biomassa è il rendimento di crescita della biomassa che, a differenza del [[#Tasso di rendimento di crescita]], tiene conto del consumo della biomassa per via della respirazione endogena.
Per questa ragione si può definire anche
Si ricorda che era
Inoltre, ricordo essere
Vediamo che rapporto c'è tra
Possiamo quindi affermare che:
E quindi, ricordando che avevamo scritto la #Produzione di Biomassa come
Per elevati valori di
In quanto ricircolo sempre la stessa biomassa e quindi non ne genero di nuova.
Si osservi che
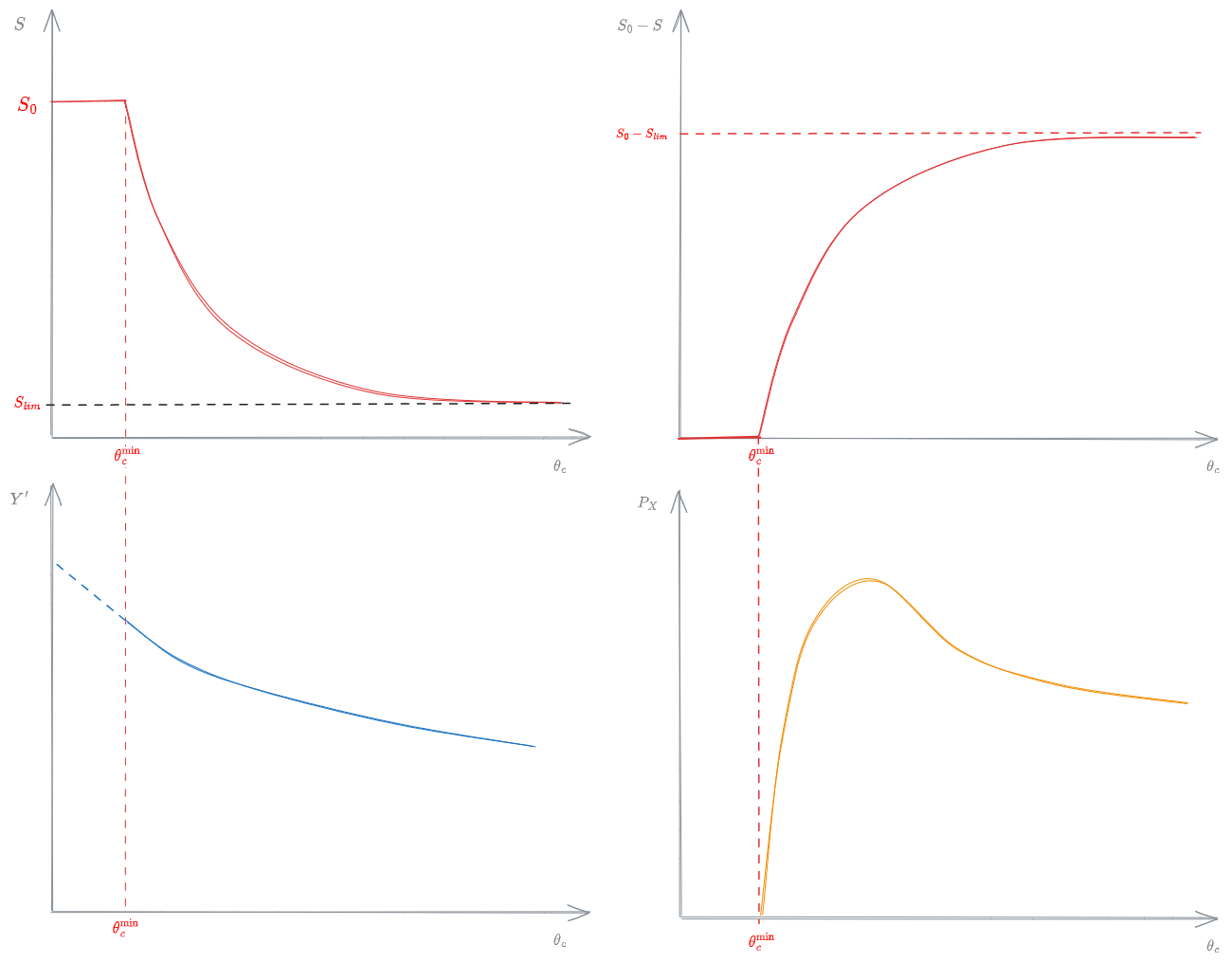
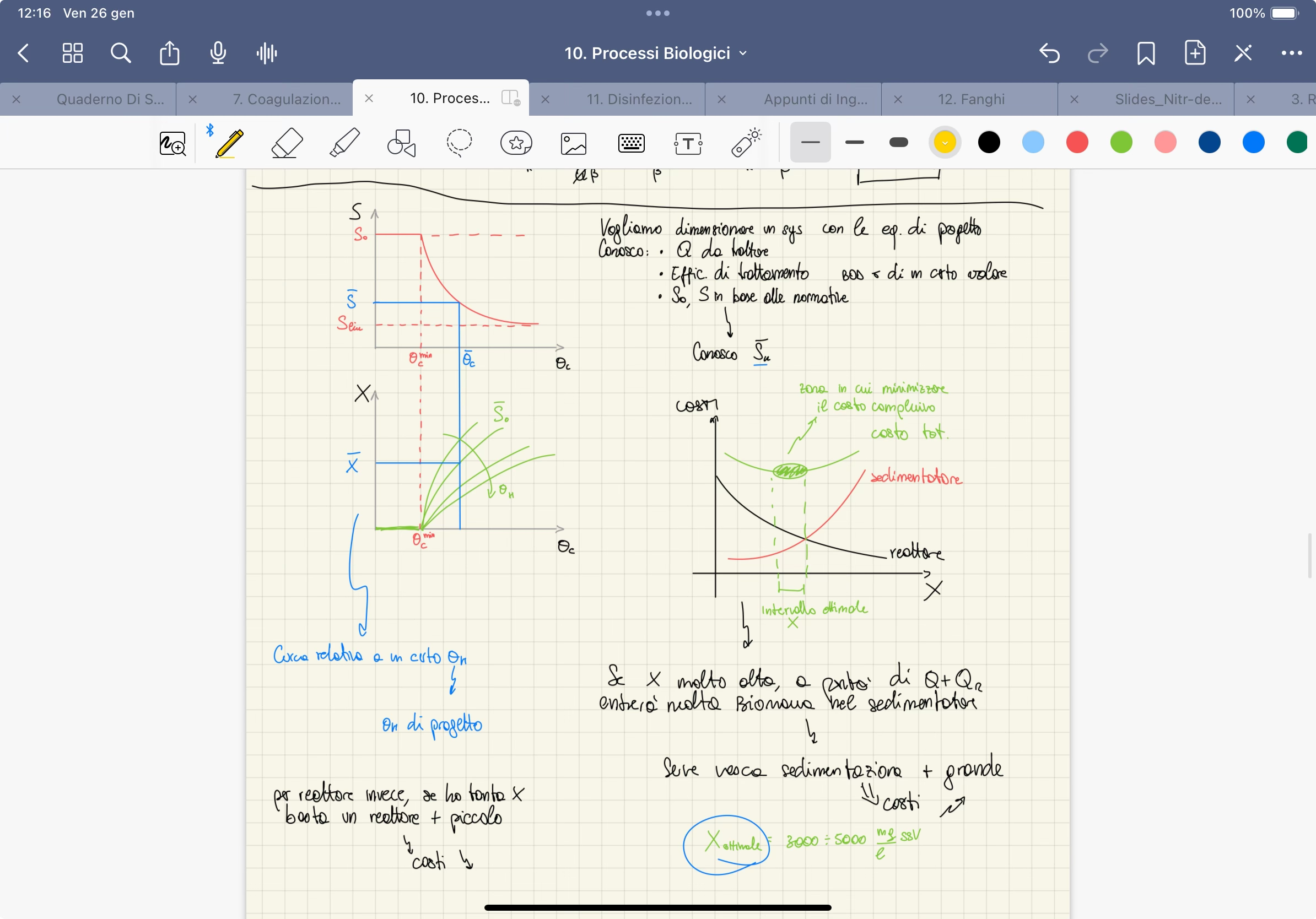
Per
Lavorare a
- Rimuovere molto substrato
- Avere tanto tempo a disposizione con poco substrato
- Questo significa presenza di respirazione endogena
Gli impianti che lavorano in queste condizioni si chiamano Impianti ad aerazione prolungata. Questo tipo di impianti si usa solo per impianti di piccole dimensioni.
- Questo significa presenza di respirazione endogena
Sistemi a fanghi attivati - con ricircolo e spurgo dal reattore
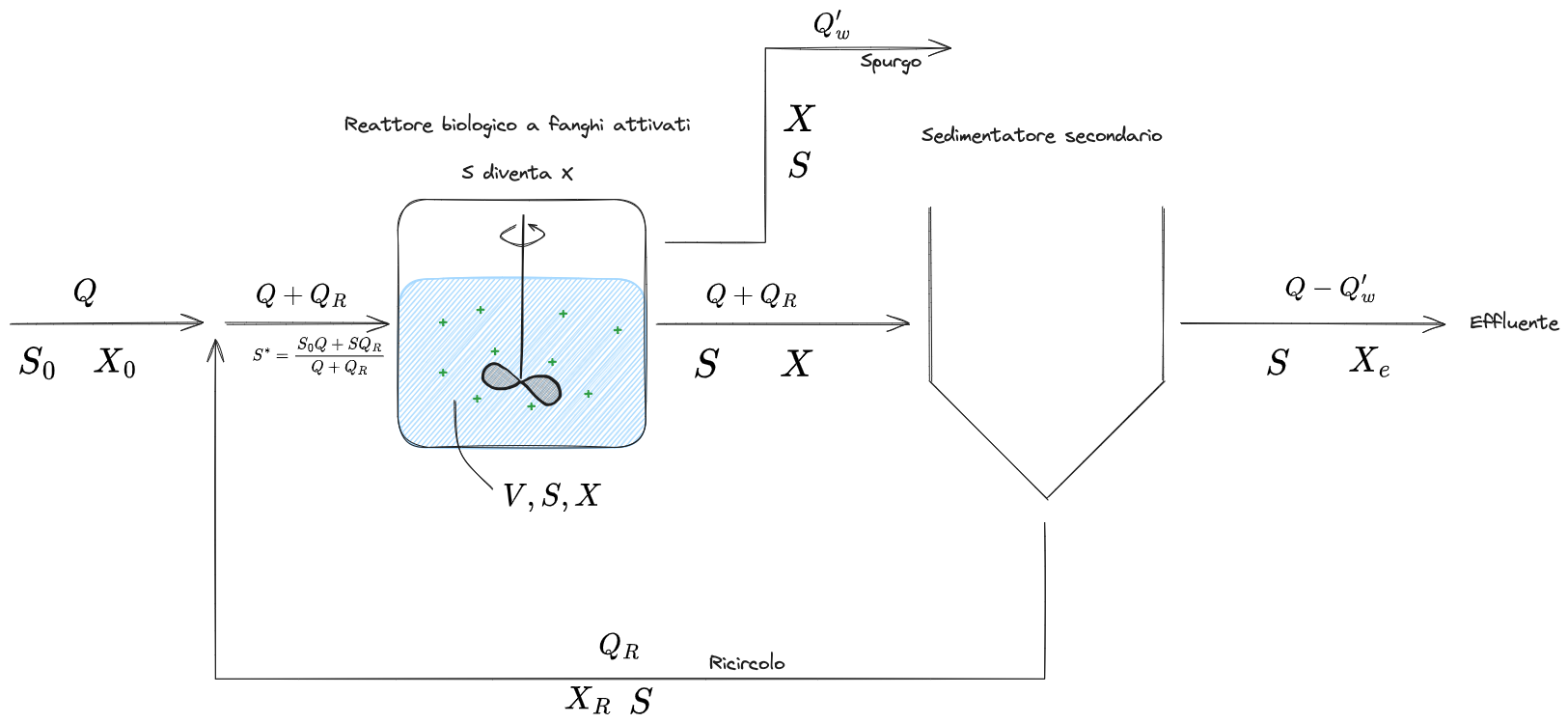
I sistemi visti fino ad ora (#Sistema a fanghi attivati - con ricircolo e spurgo dalla linea di ricircolo) prevedevano lo spurgo dei fanghi dalla linea di ricircolo.
Posso però pensare di spurgare direttamente dal reattore, una portata
Si ricorda la definizione di #Tempo di residenza cellulare:
dove possiamo riscrivere il denominatore come #Produzione di Biomassa,
Voglio confrontare il sistema con spurgo dal reattore con quello con spurgo dalla linea di ricircolo. Per farlo dovremo imporre che i due sistemi abbiano un #Tempo di residenza cellulare uguale. Avremo così due sistemi equivalenti.
- [?] Perché i due sistemi così sono equivalenti? Ossia: perché i due sistemi sono equivalenti se hanno lo stesso #Tempo di residenza cellulare?
- Il funzionamento del sistema, in termini di sub, biomassa, ecc. dipende da
. Per paragonare i due sistemi, non posso che farlo a parità di
- Il funzionamento del sistema, in termini di sub, biomassa, ecc. dipende da
Trascuro
Essendo
dovrà pertanto essere:
Si vede quindi che si dovrà mantenere uguali i rapporti tra le portate di spurgo e le concentrazioni di biomassa nello spurgo.
Avendo trascurato
Confronto tra sistemi con spurgo da ricircolo e da reattore
Si confrontano ora i #Sistemi a fanghi attivati - con ricircolo e spurgo dalla linea di ricircolo e #Sistemi a fanghi attivati - con ricircolo e spurgo dal reattore.
Si hanno:
se spurgo dalla linea di ricircolo se spurgo dal reattore
Si noti che, nel caso di spurgo dalla linea di ricircolo, per regolare lo spurgo, devo conoscere siache . Nel secondo caso invece, basta conoscere e quindi posso limitarmi a controllare la portata.
Dal punto di vista economico, conviene il #Sistema a fanghi attivati - con ricircolo e spurgo dalla linea di ricircolo perché usa portate in uscita minori.
Rapporto tra
Cerchiamo ora di capire che rapporto intercorra tra
Per farlo eseguiremo il bilancio di materia guardando esclusivamente al sedimentatore secondario.
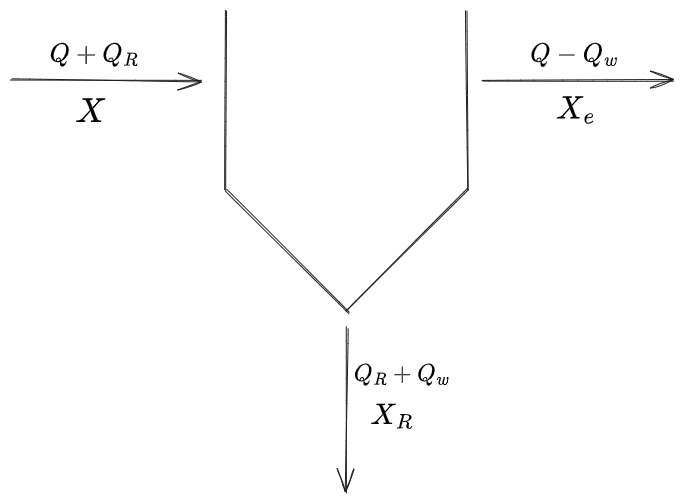
Come sempre, trascurerò il contributo dovuto alla concentrazione di biomassa nell'effluente,
Di solito inoltre, si ha che:
Posso quindi anche trascurare
Avrò pertanto, dopo le dovute semplificazioni:
Ottengo così che
Abbiamo detto
❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ dimensionamento con equazioni di progetto
❗❗❗❗❗❗❗❗❗❗❗❗❗
Richiesta di Ossigeno
Al fine di mantenere le condizioni aerobiche all'interno dei #Reattore a fanghi attivati occorre fornire ossigeno al sistema.
- Diffusori a balle
- Turbina
- Getti d'aria
In questo capitolo ci riproponiamo di calcolare la richiesta di ossigeno del sistema. Misureremo tutto in termini di richiesta biochimica di ossigeno (BOD), o meglio, di. Quest'ultimo tiene conto anche della respirazione endogena. Se faccio un bilancio di massa complessivo, teoricamente sto tenendo conto di tutti i termini in gioco.
Ricordando le ipotesi di - condizioni stazionarie
- Spurgo dal sedimentatore
eseguo il bilancio di massa:
dove
è la richiesta di ossigeno
Si noti che bisogna convertire le concentrazioni di substrato e biomassa in termini di:
Per il Substrato:
Per la Biomassa:
Riscrivo il bilancio di materia inserendo i coefficienti di conversione appena definiti:
Si ottiene così:
L'ossigeno in ingresso è associato al substrato entrante.
dove
Calcolo dei fattori di conversione
Calcoliamo il valore di
Ricordo che la Richiesta biochimica di ossigeno (BOD) è dato dall'equazione:
Quindi il
risulta
In definitiva:
Per il calcolo di
Pertanto sarà:
Ossia:
In definitiva, la richiesta di ossigeno sarà:
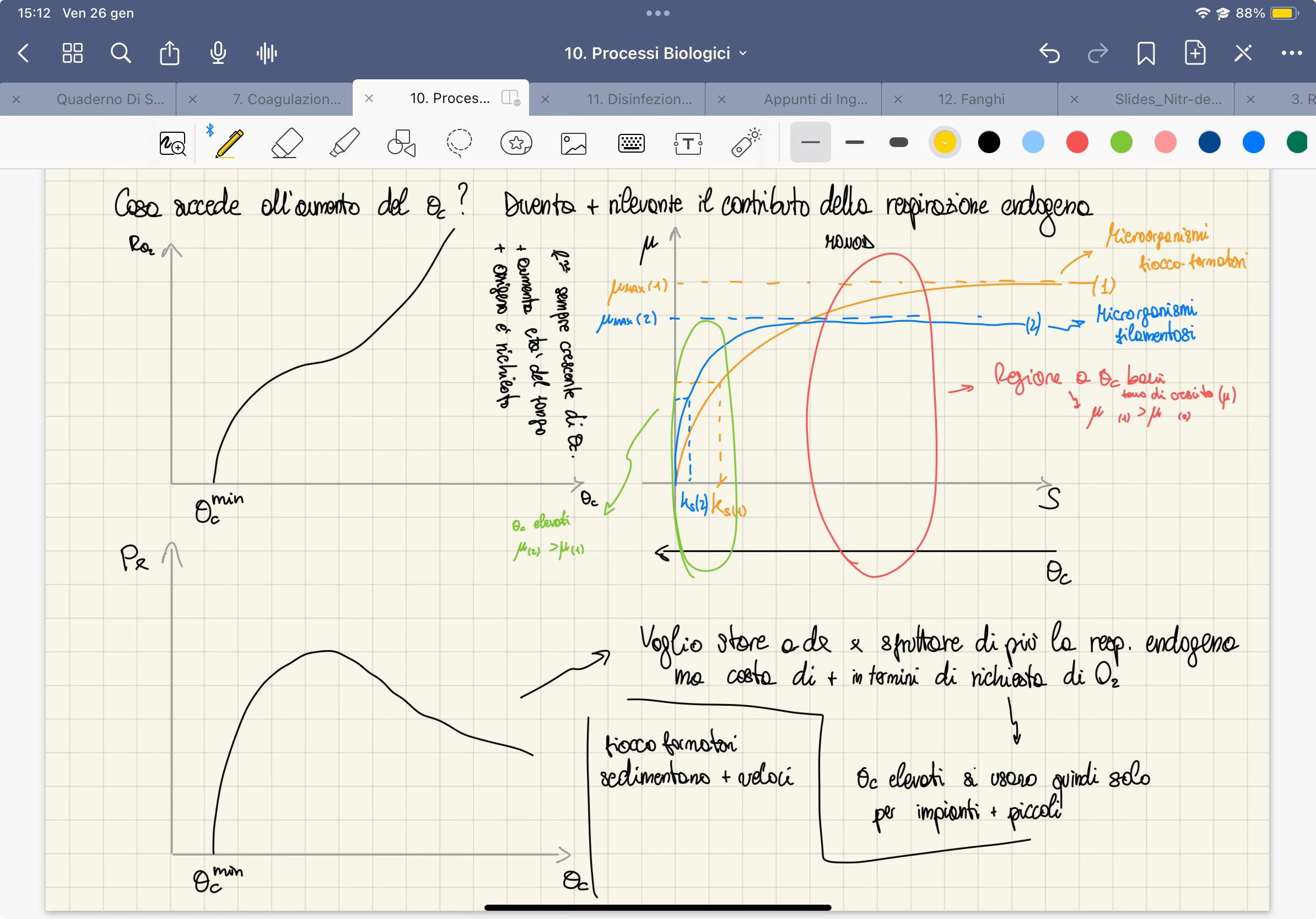
- [?] Che differenza c'è tra fiocco-formatori e filo-mentosi?
Con riferimento alla
Nel sistema non è che c'è un solo tipo di microrganismi. Ci sono milioni di tipologie diverse.
A seconda delle condizioni di funzionamento si può avere la selezione di un tipo di biomassa piuyyosto che una ltra.
in condizioni di S elevate, i microrganismi di tipo 1 sono quelli che crescono con velocità maggiore (vd. grafico scarabbocchio). Seleziona microrganismi di tipo 1. S elevati e theta_c bassi
Al contrario, in condizioni di S bassi (theta_c alti) sto in condizioni di scarso substrato. Seleziona biomassa di tipo 2.
Una curva di biomassa di tipo 2, è tipico di organismi filamentosi: curva ripida vicino l'origine, ma velocità massima minore. Si sviluppano come fossero fibre, filamenti. Hanno difficoltà a sedimentare. --> si sviluppano bulking se proliferano troppo.
Sedimentatore Secondario
Studiamo ora nel dettaglio il sedimentatore secondario.
Il sedimentatore secondario è una vasca che ha lo scopo di separare il refluo dalla Biomassa, con l'obiettivo di ottenere un refluo chiarificato.
Tipicamente il sedimentatore secondario è costituito da una vasca cilindrica con alla base un tronco di cono all'interno della quale sedimenta e si accumula la biomassa in un fango che viene poi messo in ricircolo o spurgato.
Per semplicità, si considererà questa parte di accumulo tutta concentrata in un unico punto.
Passerò quindi dalla situazione schematizzata a sinistra a quella schematizzata a destra:
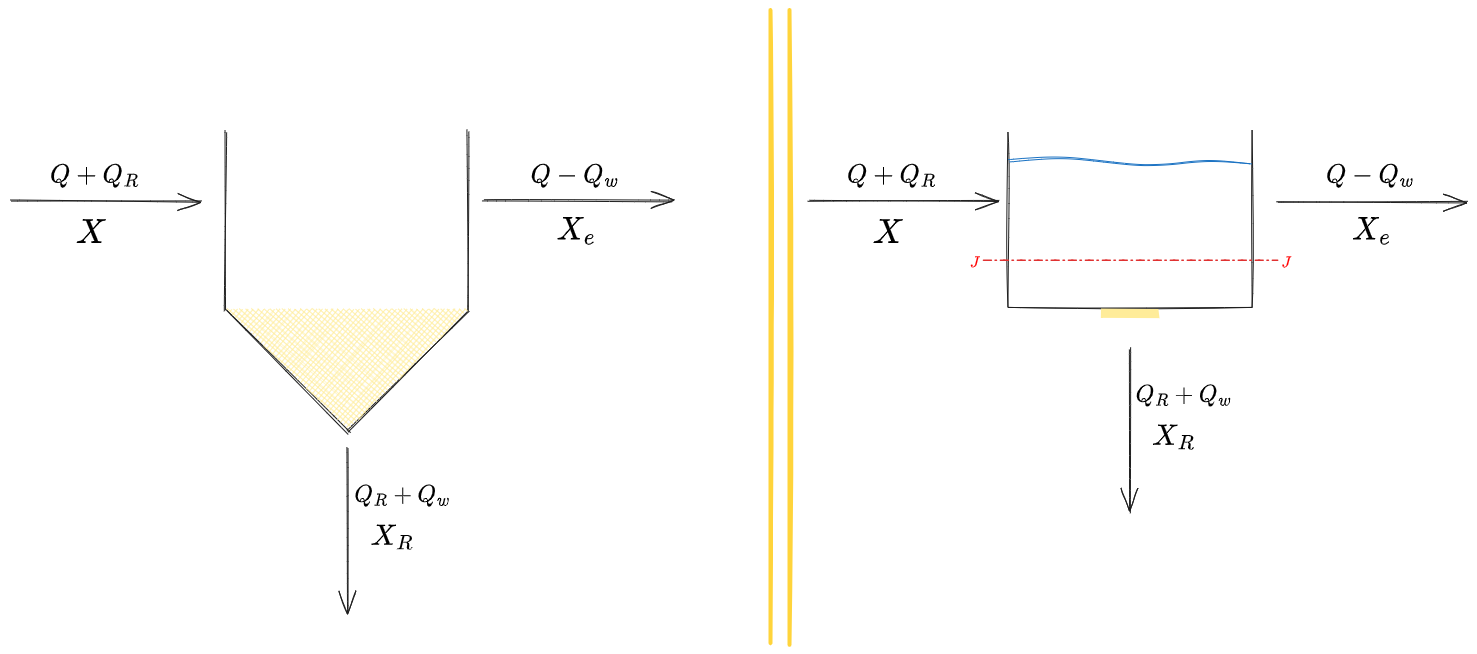
Lo studio del sedimentatore avverrà facendo riferimento alla #Teoria del Flusso Solido
Teoria del Flusso Solido
Flusso di Solidi
Il flusso di solidi è la quantità di particelle (massa) che attraversano una certa sezione (superficie) nell'unità di tempo.
Il Flusso di Solidi è esprimibile anche come una concentrazione per una velocità:
Nella #Teoria del Flusso Solido applicata ai sedimentatori, il flusso di solidi è dovuto a 2 diversi contributi:
Il contributo della gravità Il #Flusso Solido di Underflow
Il Flusso solido totale è pertanto dovuto alla somma dei due contributi appena menzionati:
Il cui andamento è mostrato sotto:
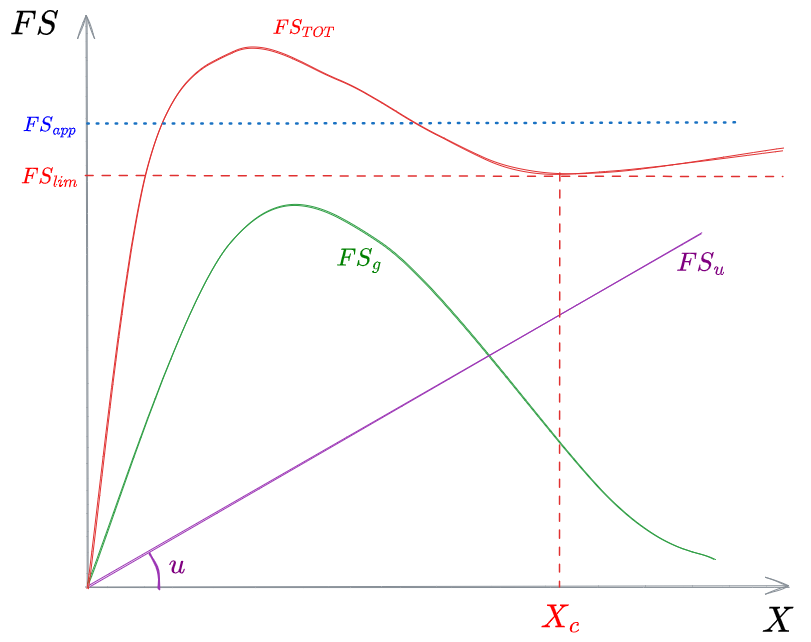
La prima parte della curva di
All'interno del sedimentatore, la concentrazione è costante sezione per sezione. Inoltre, la concentrazione aumenta man mano che ci si trova a profondità maggiori della vasca. Si può pertanto guardare alla concentrazione
La curva
Si può dire quindi che la
FLUSSO SOLIDO LIMITE
Notiamo che la curva di
FLUSSO SOLIDO APPLICATO
Se, come abbiamo detto,
Si guardi al grafico e al
Si noti che per il valore di
che è verificato se è verificata la condizione
Inoltre, al fine di sfruttare al massimo la capacità del sedimentatore, cercheremo di applicare un flusso il più grande possibile. Il che si traduce nella condizione:
FONDO DEL SEDIMENTATORE
Sul fondo del sedimentatore si avranno le seguenti condizioni:
in corrispondenza del quale si ha una concentrazione
Viene da chiedersi per quale motivo il
Per prima cosa, potremmo di ignorare
A bassi valori di
Oltre tale concentrazione, diventa molto più rilevante il contributo di #Flusso Solido di Underflow. Questo è dovuto all'aspirazione del fango dal fondo del sedimentatore. Quindi se è vero che si ha poco #Flusso Solido per gravità per via delle elevate concentrazioni, si avrà comunque un flusso totale che torna a crescere.
Coniugata della retta di underflow
Abbiamo detto che il flusso massimo che posso applicare senza incorrere in fenomeni di accumulo nel #Sedimentatore Secondario è
Abbiamo anche visto che in corrispondenza di
Spezzando
dove, essendo il [[#Flusso Solido di Underflow]]
e quindi:
Abbiamo quindi dimostrato la seguente cosa:
In corrispondenza di
Inoltre si può dimostrare che la coniugata alla retta di underflow (la retta a pendenza
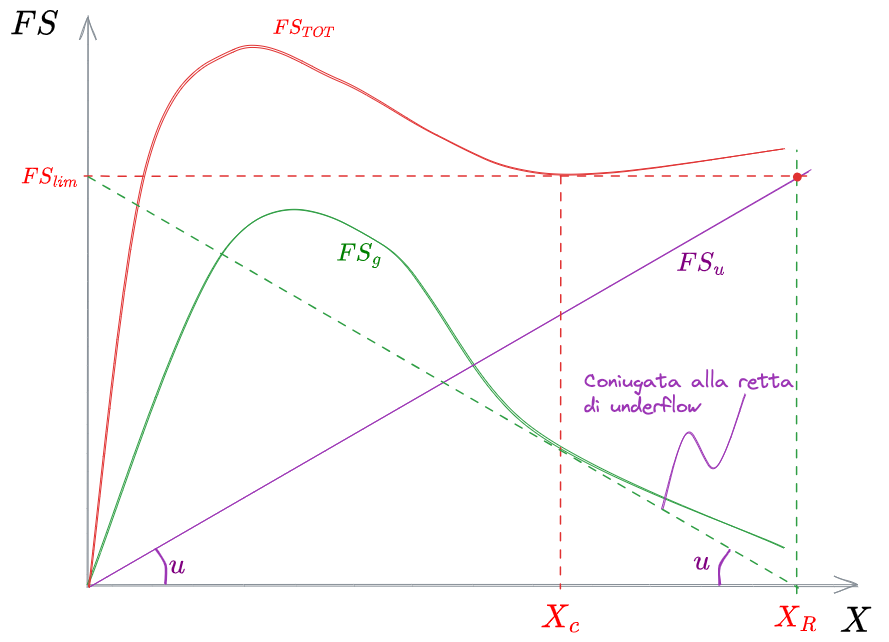
Flusso Solido per gravità
Il flusso solido solido per gravità è il contributo del #Flusso di Solidi dovuto alla sedimentazione che avviene naturalmente all'interno del #Sedimentatore Secondario.
È esprimibile come prodotto tra la concentrazione di biomassa alla sezione
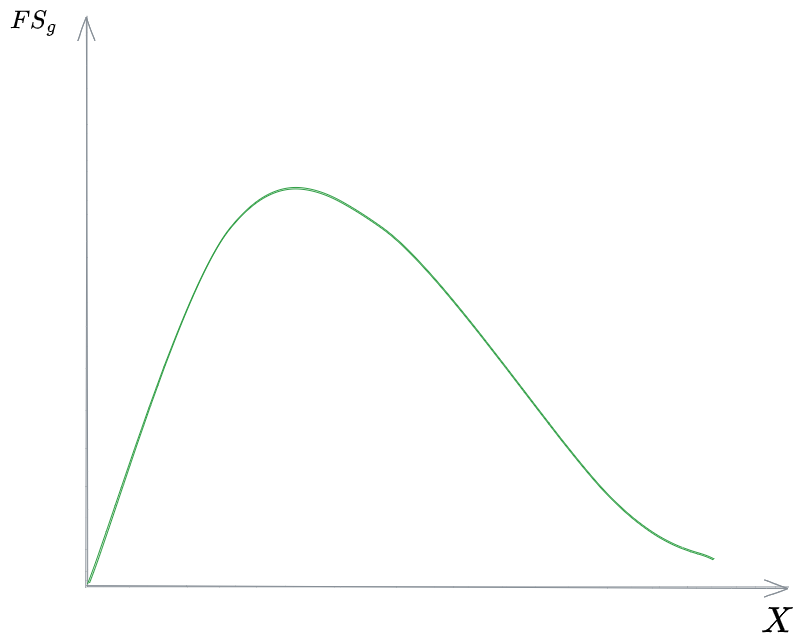
L'andamento del flusso solido per gravità è spiegato da quanto detto in merito alla velocità di sedimentazione
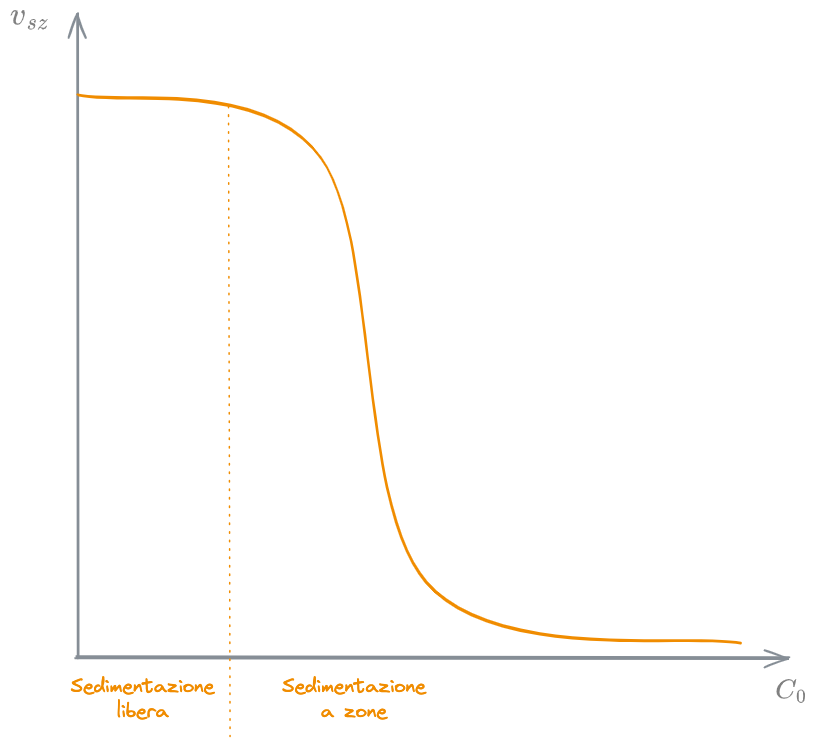
Si noti come, per valori bassi di concentrazione, la
Per elevati valori di concentrazione invece, la velocità di sedimentazione subisce una forte diminuzione, dovuta al maggiore ostacolarsi a vicenda delle particelle. Anche il
Flusso Solido di Underflow
Il Flusso Solido di Underflow è il flusso dovuto all'aspirazione causata dalla rimozione del fango alla base del sedimentatore.
È dato da:
dove
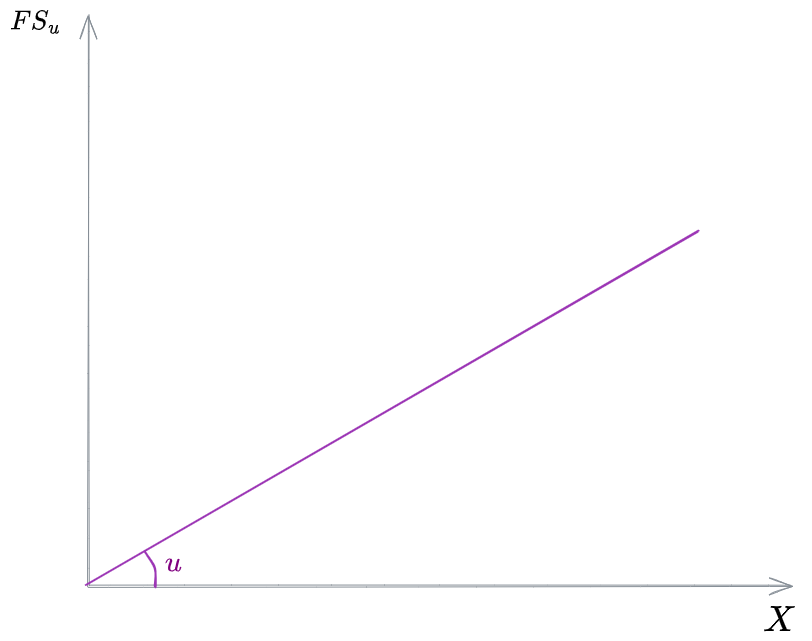
Velocità di Underflow
La velocità con cui viene estratto il fango è costante ed uguale a
Dimensionamento e gestione del sedimentatore secondario
Dimensionamento del sedimentatore
Analizziamo il #Sedimentatore Secondario.
Le grandezze note del sistema sono:
- conosciuta o assegnata (rapporto di ricircolo) e da e rapporto di ricircolo - La posso assumere - l'unica cosa nota a priori
Rimangono incognite per il dimensionamento:
Sezione del sedimentatore. Senza la sezione non possiamo conoscere le quantità legate al flusso
Nota
Questa infatti abbiamo detto ha le seguenti caratteristiche:
- Tangenza con
- Passaggio per
Esisterà una sola retta con queste caratteristiche. Trovatoposso anche tracciare .
La #Velocità di Underflow è per definizione(avendo considerato nullo il contributo di ).
Graficamente, si può calcolare
dove si è scritto
relazione che si ottiene facendo il bilancio di materia per la Biomassa:
In definitiva si avrà che
e quindi, la sezione necessaria a garantire il corretto funzionamento del sedimentatore:
Gestione del sedimentatore
Punto di Stato
La gestione del sistemi a fanghi attivati con ricircolo e spurgo dalla linea di ricircolo: capire cioè quali siano le condizioni stazionarie di funzionamento del sistema, nonché identificare l'evoluzione nel passaggio da una condizione operativa di stato stazionario a un'altra.
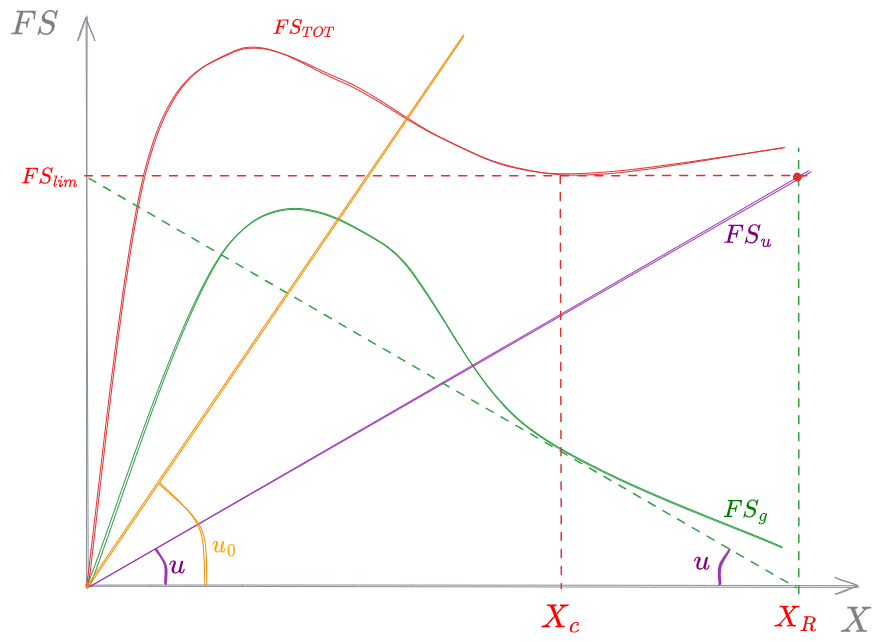
Per questo sistema è possibile definire, oltre alla già menzionata #Velocità di Underflow, una #Velocità di Overflow,
Tale velocità, identifica sul piano
- [?] Cosa rappresenta in pratica la retta di overflow? Ha a che fare con la velocità di overflow della 6. Sedimentazione?
- Retta di overflow: analoga alla retta di unnderflow ma con
invece che come pendenza. La traccio per analogia a quella di underflow. Volendola interpretare fisicamente, è dove è il flusso ascensionale dovuto al trascinamento dell'effluente. - Differenza tra velocità di overflow nella sedimentazione di tipo 1 e questa:
Il sistema in esame risulta identificato da un punto
trascurando il contributo della concentrazione dell'effluente e assumendo
Dividendo membro a membro per l'area della sezione orizzontale del sedimentatore
che diventa, ricordando le definizioni di #Velocità di Underflow e #Velocità di Overflow
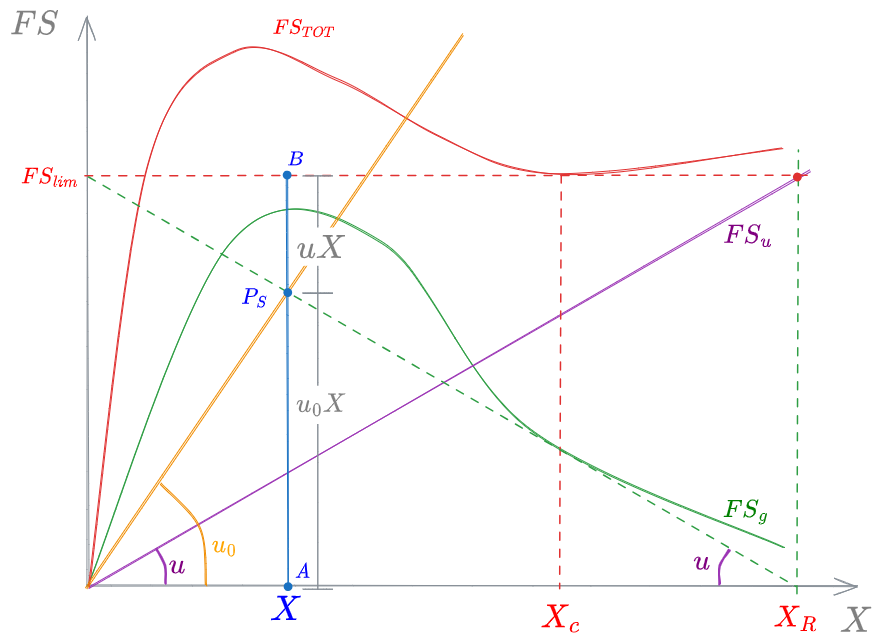
Dall'espressione appena ricavata si intuisce come, assegnato un certo valore della concentrazione di biomassa
Secondo le relazioni appena descritte risulta quindi chiaro che il punto di stato
Allo scopo di soddisfare il criterio di chiarificazione del surnatante, risulta evidente che il punto di stato debba trovarsi al di sotto della curva di
- [?] Perché, per garantire la chiarificazione (CRITERIO DI CHIARIFICAZIONE), bisogna avere punto di stato al di sotto della curva
? Perché questa condizione garantisce che la velocità di risalita del surnatante sia sempre inferiore a quella di sedimentazione del fango? Perché quest'ultima cosa garantisce la chiarificazione? - La risultante delle due velocità verticali è diretta verso il basso
Nella condizione descritta, il
Compreso che
- #Variazione della portata in ingresso
- #Variazione della concentrazione di biomassa
Le variazioni avverranno sotto le seguenti ipotesi:
- Variazione istantanea
- Le altre grandezze non variano
Variazione della portata in ingresso
Immaginiamo un'aumento della #Velocità di Overflow, dovuta ad esempio a un'aumento della portata influente
Si passerà così da
Rimarranno invece invariate le condizioni relative alla retta du Underflow e il valore della concentrazione di biomassa
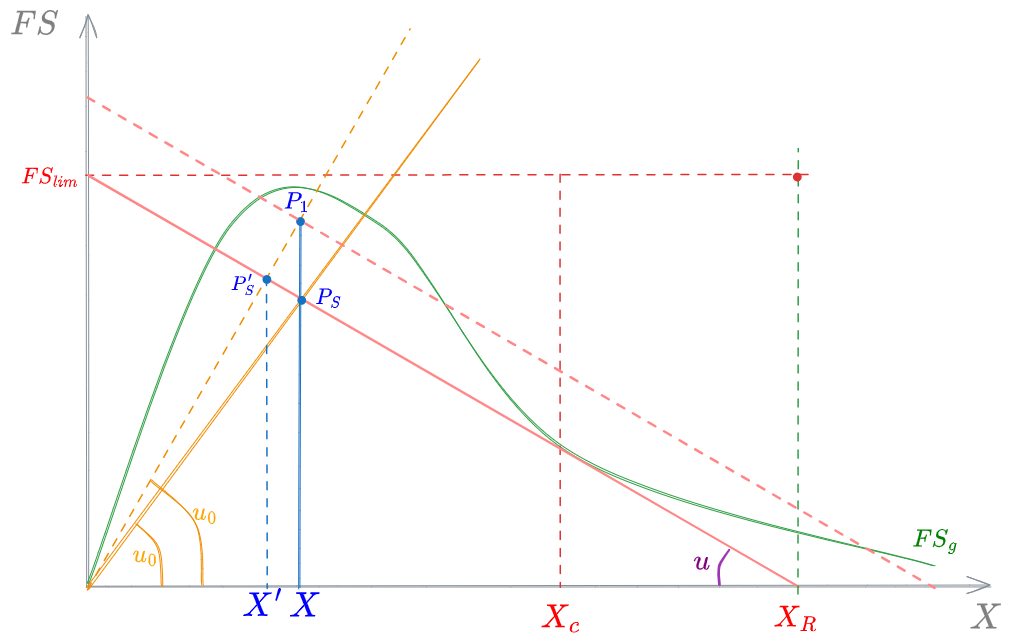
La modifica della portata influente avrà pertanto come conseguenza una traslazione della coniugata alla retta di underflow fino al punto
Il #Flusso di Solidi applicato sarà pertanto variato da
dove, essendo
Si ricorda che
Questa cosa risulta evidenziata anche dal fatto che la retta di Underflow interseca la curva di [[#Flusso Solido per gravità]]
Al fine di tornare in una condizione di equilibrio, la retta di underflow inizierà a traslare verso il basso, tornando a passare per il punto
A questo punto viene individuato un nuovo punto di stato,
In definitiva si avrà una diminuzione della concentrazione della biomassa del sistema (
Variazione della concentrazione di biomassa
Immaginiamo ora un aumento istantaneo di concentrazione di biomassa da
Rimangono invariate la pendenza della retta di Underflow (
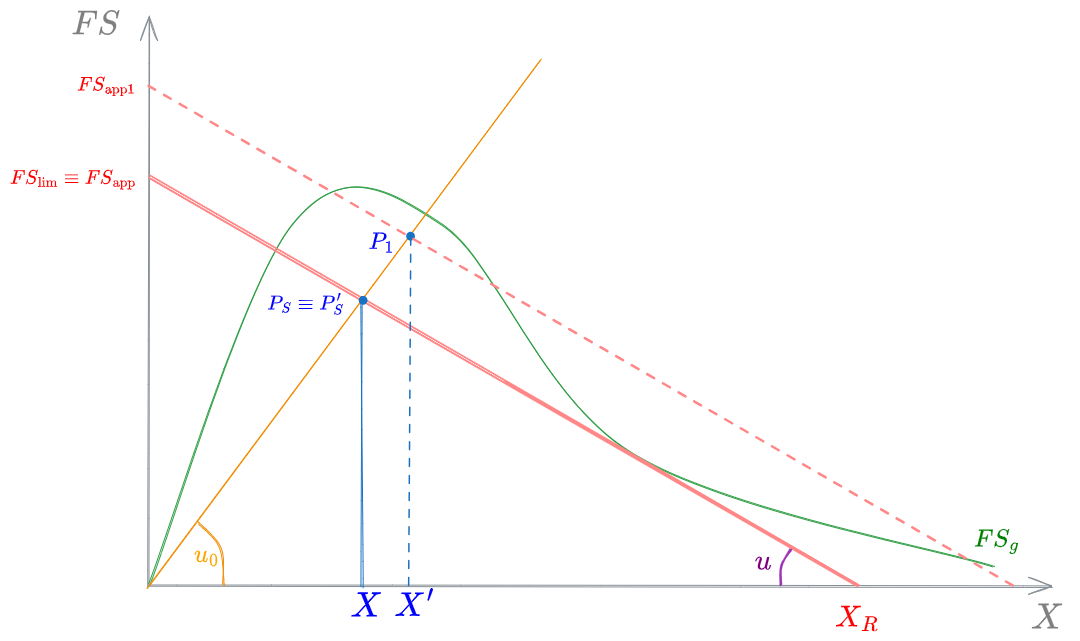
Come conseguenza si avrà una traslazione verso l'alto della retta di Underflow.
Notiamo che, come nel caso di #Variazione della portata in ingresso, in questa condizione la retta di underflow interseca la curva di [[#Flusso Solido per gravità]]
In particolare, il nuovo [[#Flusso di Solidi]] applicato sarà:
Il raggiungimento delle condizioni di stato stazionario si avrà esclusivamente quando la retta di underflow tornerà a traslare verso il basso per riportare il nuovo punto
- [?] Perché nonostante il punto di stato sia tornato al punto di stato precedente, le condizioni nel sistema sono variate?
Dal punto di vista del sedimentatore è la stessa condizione: stessa
La
Non è detto che questo
Questo è un problema dal punto di vista dell'eliminazione del substrato, non della sedimentazione della biomassa.