06. Sedimentazione

6. Sedimentazione

La sedimentazione è il principale processo di depurazione delle acque. È un processo che si basa sulla gravità per rimuovere le particelle solide dal fluido.

osservazione

Qualora la densità del fluido risulti superiore a quella delle particelle, si sfrutta per la depurazione un processo analogo, detto flottazione.

La sedimentazione può essere separata in 4 meccanismi, sulla base della concentrazione dell'agente inquinante.

Tipo 1: #Sedimentazione libera
Tipo 2: #Sedimentazione per Flocculazione
Tipo 3: #Sedimentazione a zona
Tipo 4: #Sedimentazione per Compressione

[?] Non ho capito il discorso del contenitore inclinato, isobare ecc.
- Ho chiesto ma non ho ancora capito

Sedimentazione libera

sedimentazione libera

È la sedimentazione che avviene in condizioni di particelle isolate. Queste sedimentano per gravità senza che vi sia alcuna interazione tra le particelle. Ogni particella sedimenta come se fosse da sola.

Si considera una particella isolata di diametro $D$ . Ammesso che la sua densità risulti maggiore di quella del liquido, questa tenderà a muoversi verso il basso.

Le forze in gioco sono:

Forza di Archimede - Dovuta alla differenza di pressione tra i due estremi della particella
Forza di Inerzia - Verso opposto all'accelerazione
Forza di attrito viscoso
Forza peso

Sia $m_{L}$ la massa del liquido con lo stesso volume della particella. Il bilancio delle forze fornisce:

\begin{aligned} F_{i} & = P - F_{A} - F_{R} \\ m_{s} \frac{d v}{d t} & = m_{s} g - m_{L} g - C_{D} ρ_{L} \frac{v^{2}}{2} S \end{aligned}

dove

$C_{D} =$ Coefficiente di attrito idrodinamico
$ρ_{L} =$ Densità del liquido
$S = \frac{π D^{2}}{4} =$ Superficie che genera attrito (sezione maestra)

In generale, la $F_{R}$ dipende da:

F_{R} = f (\frac{v^{2}}{2}, ρ, μ, S, R e)

Essendo $V = \frac{1}{6} π D^{3}$ il volume della particella (considerata una sfera) e $ρ_{s}$ la sua densità, si può scrivere la massa della particella come:

m_{s} = ρ_{s} V

Il bilancio delle forze diventa così:

\begin{aligned} ρ_{s} \frac{1}{6} D \frac{d v}{d t} & = ρ_{s} \frac{1}{6} π D^{2} g - ρ_{L} \frac{1}{6} π D^{3} g - C_{D} ρ_{L} \frac{v^{2}}{2} π \frac{1}{4} D^{2} \\ ρ_{s} \frac{1}{3} D \frac{d v}{d t} & = g \frac{1}{3} D (ρ_{s} - ρ_{L}) - C_{D} ρ_{L} v^{2} \frac{1}{4} \end{aligned}

Questa si potrebbe integrare per ottenere la $v (t)$ . Immaginiamo però di metterci nelle condizioni stazionarie in cui la velocità della particella ha raggiunto la velocità terminale:

v = v_{l i m} ⟹ \frac{d v}{d t} = 0, v = cost = v_{l i m}

per cui

0 = g \frac{1}{3} D (ρ_{s} - ρ_{L}) - C_{D} ρ_{L} v_{l i m}^{2} \frac{1}{4}

da cui si ottiene, risolvendo l'equazione algebrica, l'#Equazione di Newton

Equazione di Newton

Nella #Sedimentazione libera, si descrive la velocità terminale di una particella isolata con la seguente equazione:

equazione di newton

$v_{l i m} = \sqrt{\frac{4 g (ρ_{s} - ρ_{L}) D}{3 C_{D} ρ_{L}}}$

Il $C_{D}$ si può considerare uguale a

C_{D} = \frac{24}{R e} + \frac{3}{\sqrt{R e}} + 0.34

con Numero di Reynolds pari a:

Re = \frac{ρ_{L} v D}{μ} = \frac{v D}{ν}

dove:

$μ =$ Viscosità dinamica del fluido
$ν = \frac{μ}{ρ_{L}} =$ Viscosità cinematica del fluido

osservazione

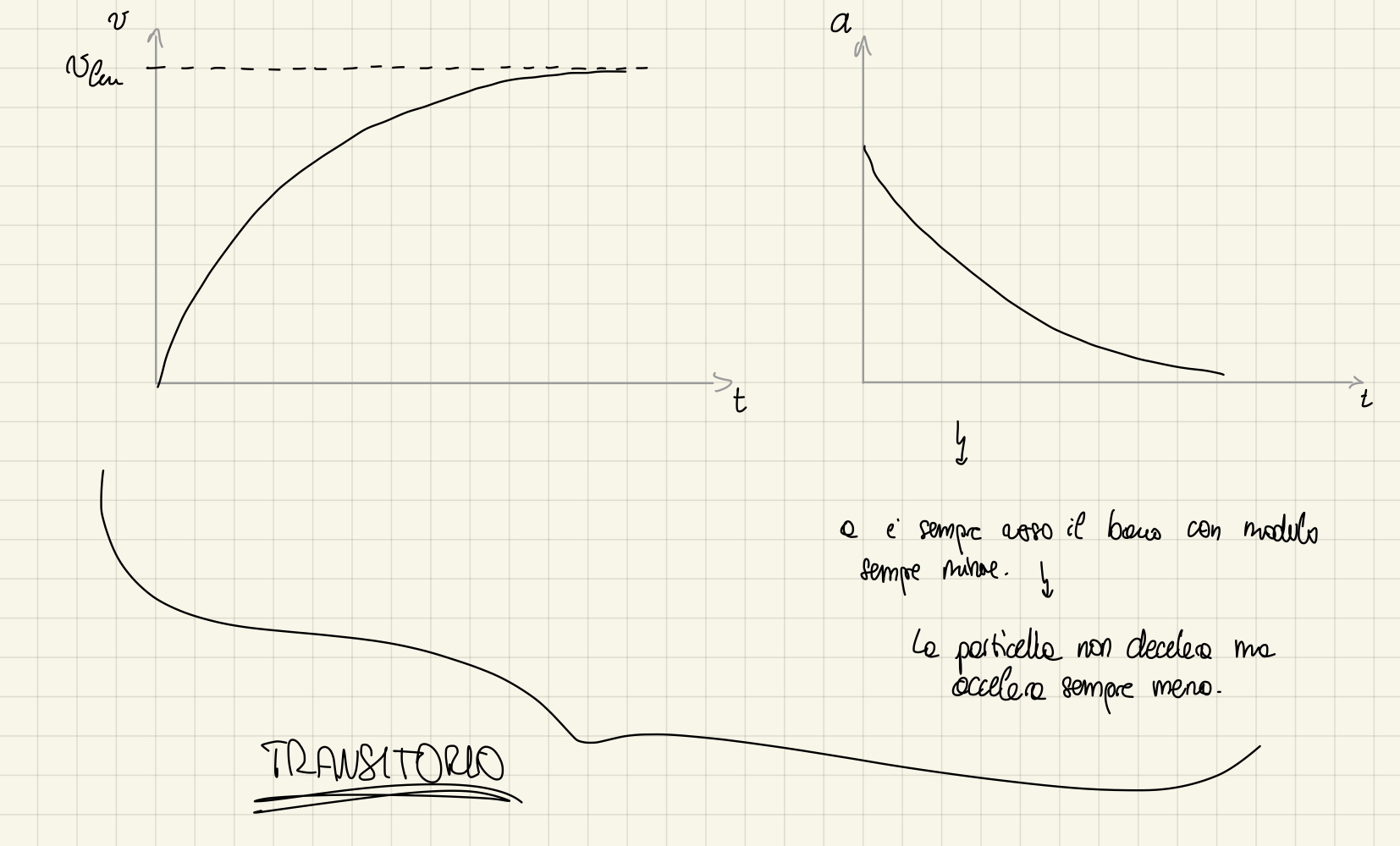
Si noti che l'#Equazione di Newton è implicita rispetto alla velocità. Per risolverla andrebbero usati dei metodi numerici. Se però si suppone che ci si trovi in condizioni di [[Moto Laminare]] si può semplificare.
$R e < 0.3 C_{D} ≃ \frac{24}{R e} = \frac{24 μ}{ρ_{L} v D}$

Sostituendo nell'#Equazione di Newton:

v_{l i m} = \sqrt{\frac{4}{3} \frac{ρ_{s} - ρ_{L}}{ρ_{L}} g D \frac{ρ_{L} v_{l i m} D}{24 μ}}

che semplificando e risolvendo per $v_{l i m}$ diventa la cosiddetta #Equazione di Stokes

Equazione di Stokes

equazione di stokes

$v_{l i m} = \frac{1}{18} g \frac{(ρ_{s} - ρ_{L}) D^{2}}{μ}$

che è conosciuta come #Equazione di Stokes.

Quando si studia la #Sedimentazione libera, si procede come segue:

Suppongo moto laminare
Applico l'#Equazione di Stokes
Verifico se $R e < 0.3$
- Se $R e > 0.3$ applico l'#Equazione di Newton

Per farlo uso un metodo che seppure grezzo permette di calcolare la velocità limite in maniera abbastanza semplice.
Si usa l'#Equazione di Stokes. Si calcola con la nuova velocità ottenuta Reynolds e se ancora non è verificata l'ipotesi di moto laminare si ripete. Si va avanti fino a quando due valori consecutivi di velocità non abbiano distanza inferiore a una tolleranza scelta a priori.

| v_{l i m}^{(i)} - v_{l i m}^{(i - 1)} | < ε

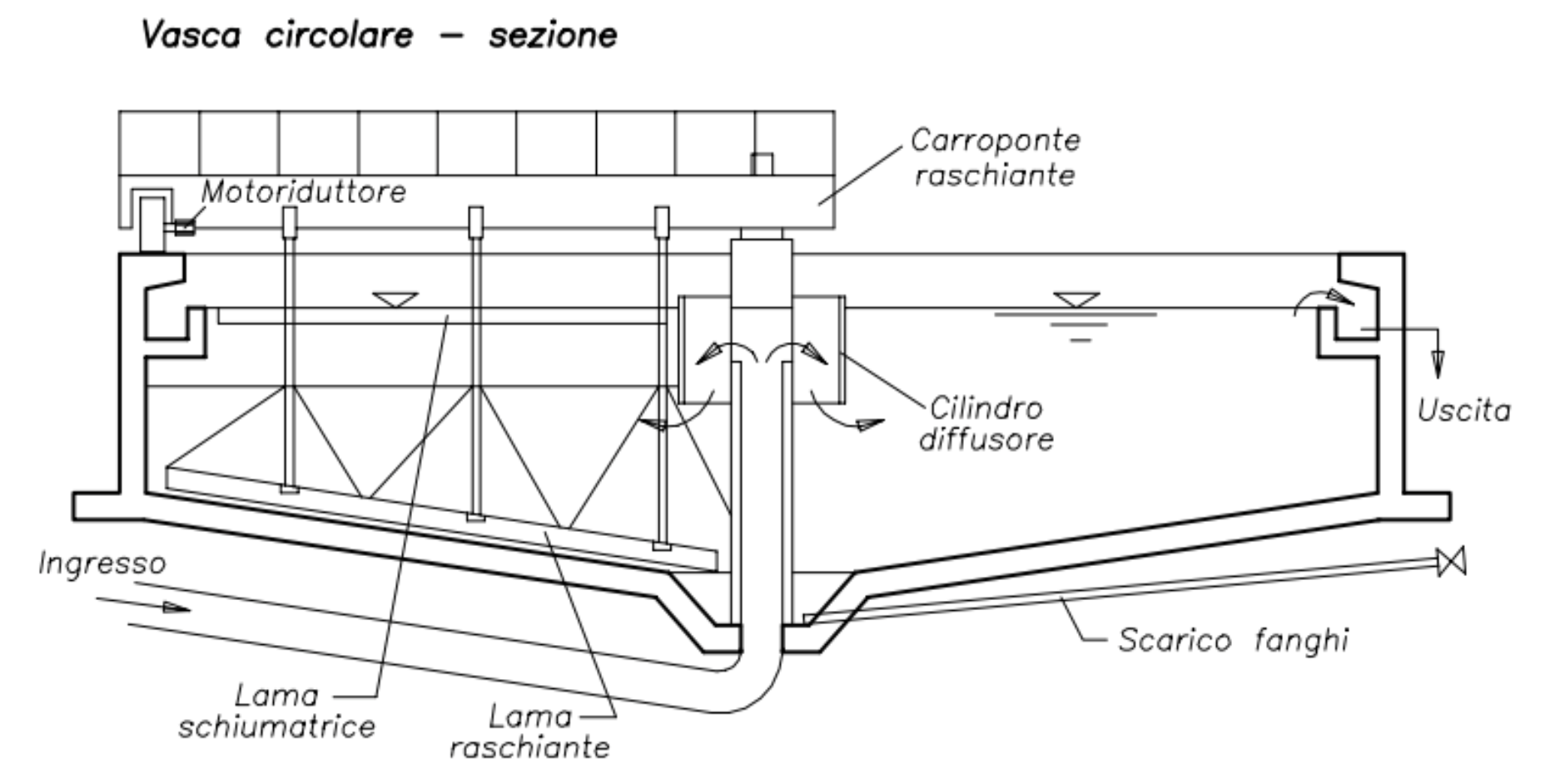
Vasca di dissabbiatura

Solitamente, la #Sedimentazione libera riguarda principalmente le sabbia.

Si ha quindi una vasca di dissabbiatura. Si considera la vasca di forma rettangolare (un parallelepipedo in 3D). In questa vasca entra una portata $Q$ a concentrazione $C_{0, S S T}$ ed esce la stessa portata a concentrazione $C_{u, S S T}$ .
ST
La parte sedimentata prende il nome di Fango.
Si suppone che il fango non venga risollevato una volta raggiunto il fondo.
La vasca è un parallelepipedo di dimensioni $L \times B \times H$

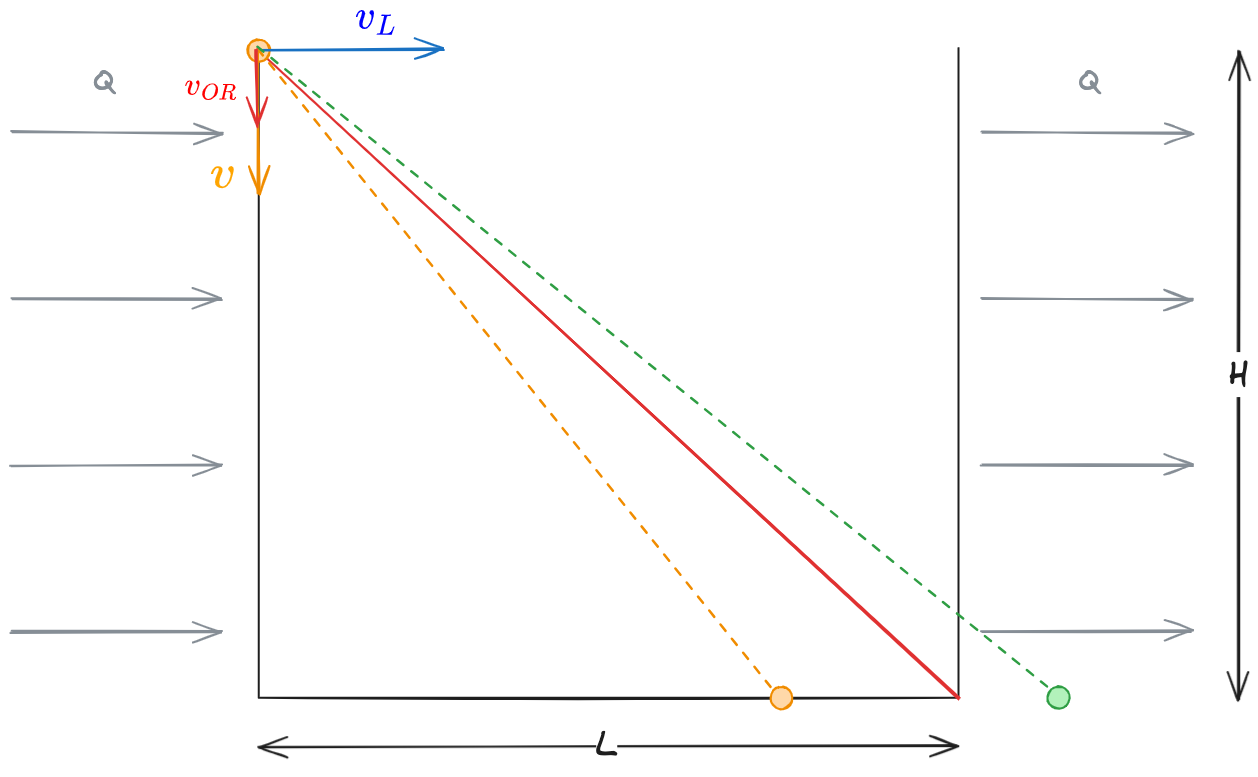
Si guardi alla vasca sopra - si trascura lo strato limite...
Come conseguenza della portata $Q$ , il liquido si muove orizzontalmente (e allo stesso modo la particella se si suppone che non ci sia slittamento tra solido e liquido) a velocità orizzontale $v_{L}$ . Sia $v$ la velocità verticale delle particelle.
Alcune particelle toccheranno il fondo entro la lunghezza $L$ , altre invece andranno oltre.

Ci interessa la particella che raggiunge il fondo proprio alla fine della vasca (segue traiettoria coincidente con la diagonale della vasca). La velocità verticale di questa particella la chiamiamo $V_{O R}$ (#Velocità di Over Flow - Carico idraulico Superficiale).

Se $v_{s} \geq v_{O R}$ tutte le particelle sedimentano entro la lunghezza della vasca --> L'inquinante è rimosso completamente
Se $v_{s} < v_{O R}$ non tutte le particelle sedimentano entro la lunghezza della vasca. Alcune che entrano a quota minore potrebbero riuscire a sedimentare, oltre una certa quota, non sedimentano più.

Mettiamoci nel secondo caso e trasliamo tutte le traiettorie in modo che tutte le particelle sedimentino entro $L$ .
Otterremo una quota, $h_{2}$ , entro la quale le particelle vengono completamente rimosse. Le particelle oltre tale quota, invece, non vengono rimosse.

ipotesi

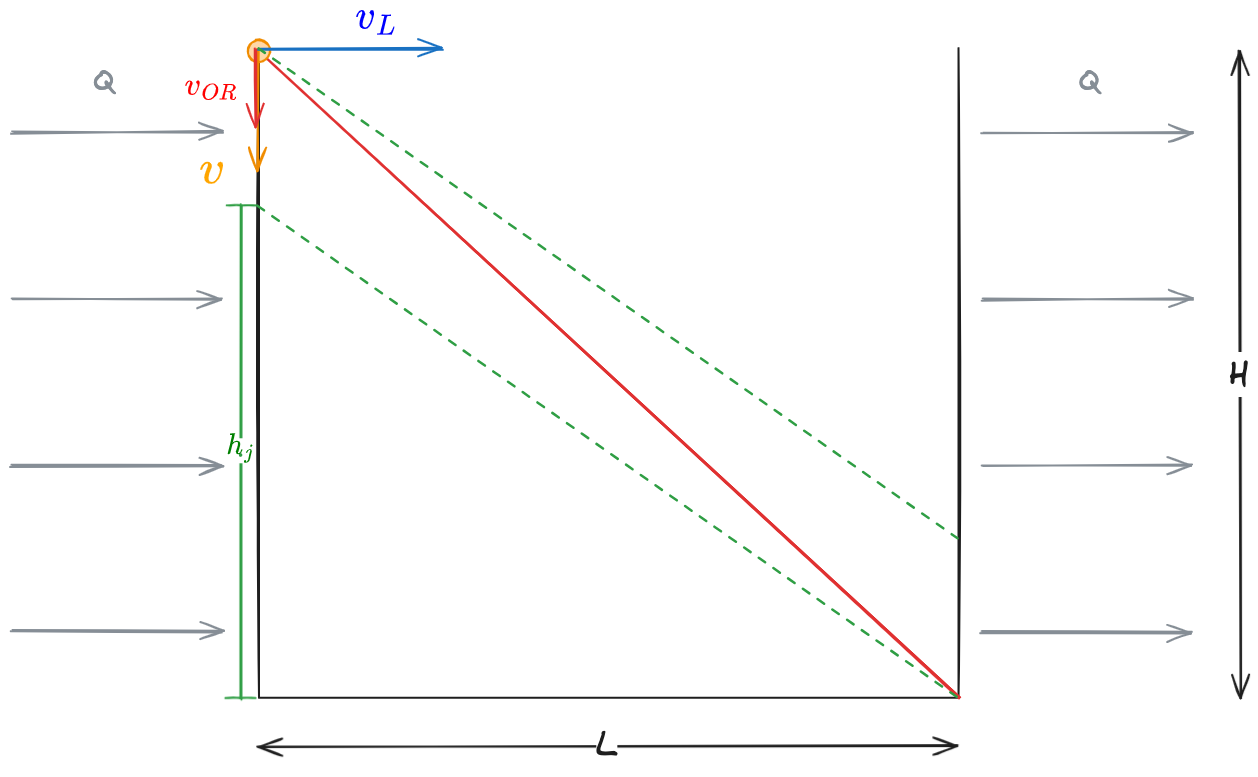
Si suppone di avere una distribuzione uniforme di particelle lungo l'altezza.

Si definisce il #Rapporto di Rimozione

r_{j} = \frac{h_{j}}{H}

Le particelle, impiegano un tempo $θ_{H} = \frac{L}{v_{L}}$ per uscire dal reattore

r_{j} = \frac{h_{j}}{H} = \frac{v_{s j} θ_{H}}{v_{O R} θ_{H}} = \frac{v_{s j}}{v_{O R}}

Quindi si può scrivere il rapporto di sedimentazione come rapporto tra la velocità di sedimentazione della particella $j$ e la velocità di Over-Flow.

v_{O R} = \frac{H}{θ_{H}} = \frac{H}{\frac{V}{Q}} = \frac{Q H}{B H L} = \frac{Q}{B L} = \frac{Q}{A_{o r i z z}}

dove:

$B L =$ Sezione orizzontale della vasca

v_{L} = \frac{Q}{B H}

dove:

$B H =$ Sezione di ingresso verticale

Curva di Distribuzione Dimensionale - CDD

Si mostra sotto la Curva di Distribuzione Dimensionale - CDD (Curva granulometrica) che mostra la distribuzione, sulla base del diametro, delle particelle di solido da rimuovere.

$P^{*}$ è la percentuale di particelle con diametro $D < D^{*}$ .

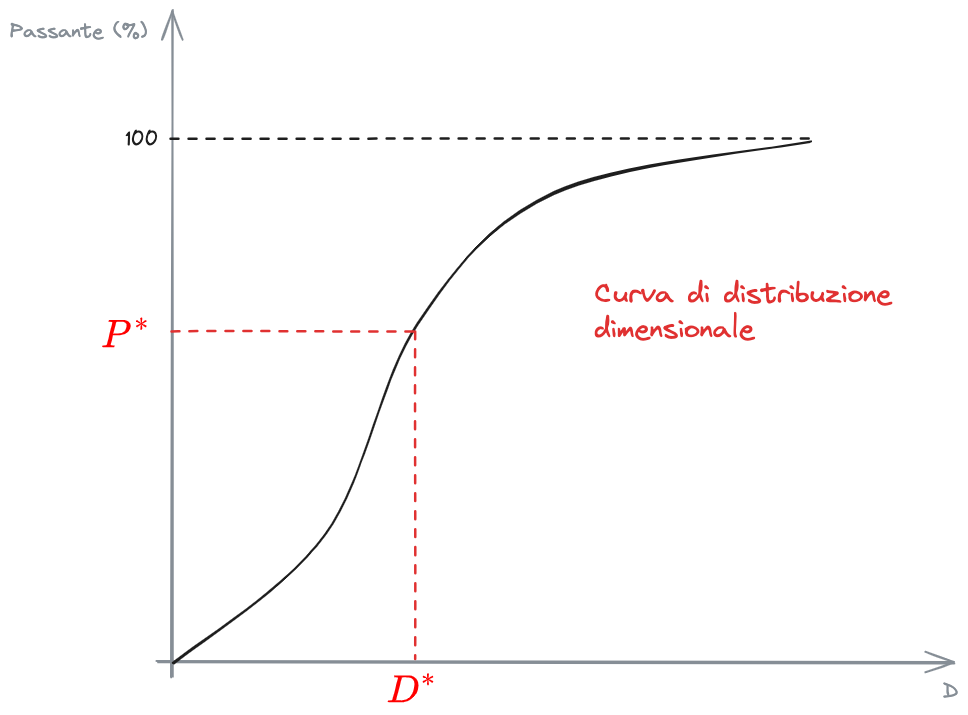
Curva Velocità di Sedimentazione - CVS

Tramite le relazioni di Newton o Stokes è noto il rapporto che intercorre tra le quantità $D$ e $v_{s}$ , per cui si traccia il grafico di percentuale di passante in funzione di $v_{s}$ .

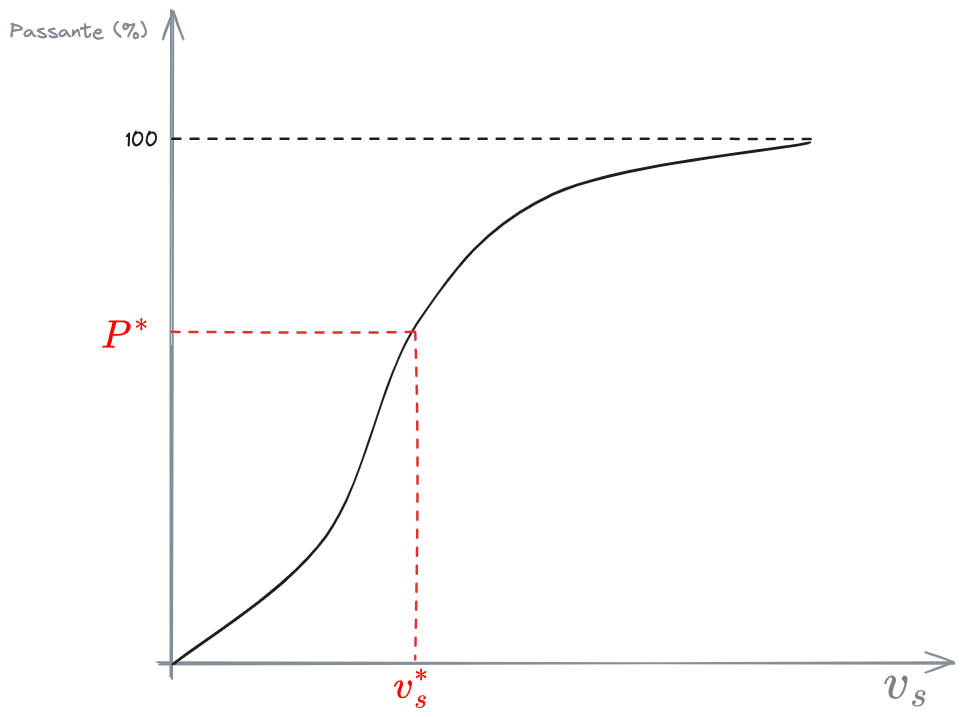
In questo ultimo caso $P^{*}$ è la percentuale di particelle con velocità di sedimentazione inferiore a $v_{s}^{*}$

Efficienza di rimozione

Supponendo di avere $v_{s} \geq v_{O R}$ , si ha che la porzione rappresentata dalla parte di curva sopra a $P^{*}$ è rimossa completamente mentre la parte inferiore è rimossa solo parzialmente, in quantità date dal #Rapporto di Rimozione $r_{j}$ .

$P_{O R}$ è la percentuale di particelle che, hanno velocità di sedimentazione minore o uguale alla velocità di over-flow: $v_{s} \leq v_{O R}$ .
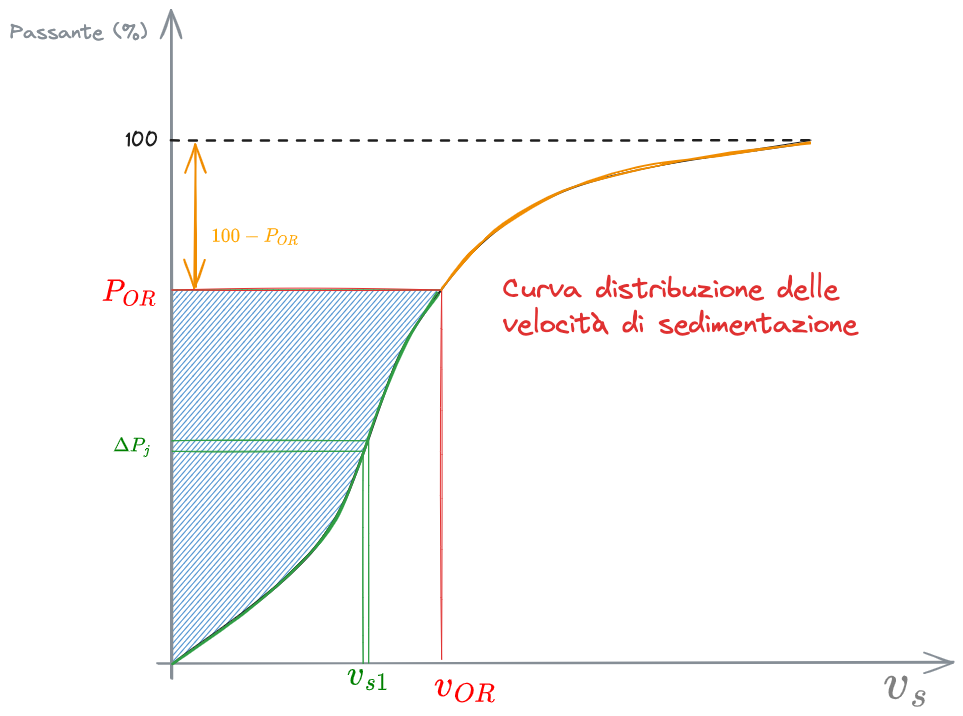
Quindi, $100 - P_{O R}$ è la percentuale di particelle con $v_{s} \geq v_{O R}$ e quindi che sarà sicuramente sedimentata.

Dobbiamo

Efficienza totale

\begin{array}{r} E = (100 - P_{O R}) + (r_{j} Δ P_{j} + r_{k} Δ P_{k}) \\ = (100 - P_{O R}) + \sum_{j = 1}^{N} r_{j} Δ P_{j} \end{array}

dove:

$N =$ il numero di intervalli complessivi

Immaginando di prendere infiniti intervalli $Δ P$ avremmo che

\begin{array}{r} N \to \infty \\ Δ P \to d p \end{array}

e si potrebbe riscrivere l'efficienza come:

\begin{aligned} E & = (100 - P_{O R}) + \int_{0}^{P_{O R}} r d P = \\ = (100 - P_{O R}) + \int_{0}^{P_{O R}} \frac{v_{s}}{v_{O R}} d P = \\ = (100 - P_{O R}) + \frac{1}{v_{O R}} \int_{0}^{P_{O R}} v_{s} d P \end{aligned}

In definitiva...

efficienza di rimozione ($e$)

Si definisce Efficienza di rimozione:
$E = (100 - P_{O R}) + \frac{1}{v_{O R}} \int_{0}^{P_{O R}} v_{s} d P$

e rappresenta la percentuale di particelle che viene rimossa da una certa [[#Vasca di dissabbiatura]] la cui [[#Velocità di Over-FLow]] sia $v_{O R}$ e con una assegnata Curva di Distribuzione Dimensionale.

Se la $v_{O R}$ è piccola, l'efficienza è alta.

osservazione

Si noti che $v_{O R} = \frac{Q}{B L}$ risulta indipendente da $H$ . Sembrerebbe quindi che, indipendentemente dall'altezza della vasca, si avrebbe comunque la stessa #Efficienza di rimozione. È evidente però, osservando il sistema, che cambiando $H$ e mantendo invariate tutte le altre quantità, la traiettoria che prima coincideva con la diagonale, ora porta a un punto esterno alla vasca.
Quando si varia la sezione, seppure è vero che la $v_{O R}$ rimane invariata, cambia la velocità del liquido $v_{L}$ , essendo questa $v_{L} = \frac{Q}{B H}$ .

Seppure sembrerebbe che avere degli $H$ estremamente bassi possa solo portare dei beneifici, in realtà ci sono delle controindicazioni:

Si rischia di avere risollevamento del fango
Serve comunque uno spessore minimo per l'accumulo dei fanghi
Gli effetti della turbolenza o del rimescolamento per azione del vento non sono più trascurabili

Tipicamente si usano vasche dell'altezza di $H \sim 2 \div 3 m$ .

Descrizione sperimentale della sedimentazione libera

Si descrive ora in maniera empirica il processo di #Sedimentazione libera (tipo 1).

Si sfrutta per lo scopo un cilindro graduato (colonna di sedimentazione) che si comporterà da Reattore batch, non essendoci ingresso ne uscita di materiale.

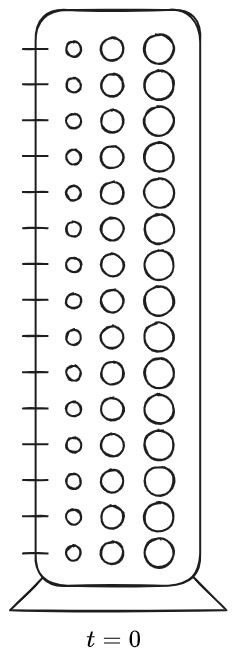
All'interno del cilindro graduato è posto un refluo con particelle a diversa distribuzione granulometrica. Si considera all'istante iniziale $t = 0$ la concentrazione all'interno della colonna come uniforme (condizioni di perfetta miscelazione). Si osserva quindi l'evoluzione del processo di sedimentazione nel tempo.

Si immagini di discretizzare il problema considerando un numero finito di strati e ipotizzando che all'interno di ognuno di essi siano presenti 3 particelle di dimensioni diverse, aventi rispettivamente diametri $D_{1}, D_{2}$ e $D_{3}$ tali che $v_{2} = 2 v_{1}$ e $v_{3} = 3 v_{1}$ .

La situazione all'istante iniziale $t = 0$ all'interno della colonna di sedimentazione è la seguente:

Se in un certo intervallo di tempo $Δ t$ la particella $D_{1}$ percorre uno spazio $h_{1}$ , nello stesso tempo le altre particelle percorreranno rispettivamente $D_{2} ⟹ h_{2} = 2 h_{1}$ e $D_{3} ⟹ h_{3} = 3 h_{1}$ .

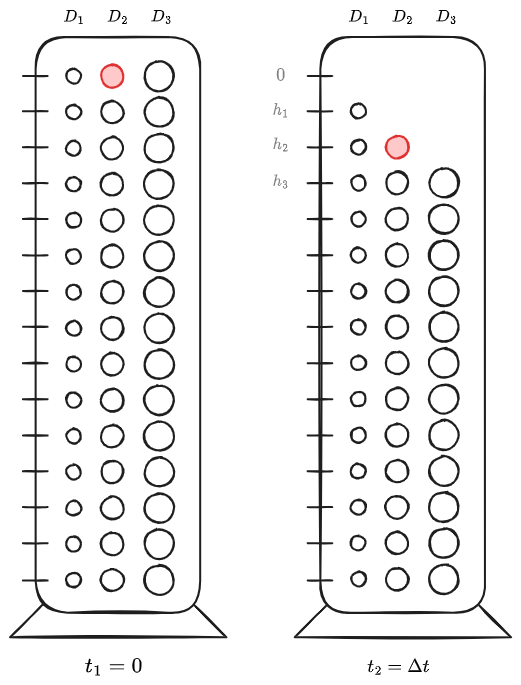
Si pone l'attenzione sulla particella di diametro intermedio, $D_{2}$ . All'istante $t = Δ t$ , all'altezza $h_{2}$ , saranno presenti solo particelle con diametro $D \leq D_{2}$ .
All'istante $t = Δ t$ saranno pertanto state rimosse, all'altezza $h_{2}$ , tutte le particelle con diametro $D > D_{2}$ .
Si può quindi definire, a $t = Δ t$ e $h = h_{2}$ , un'#Efficienza di rimozione $E_{2}$ .

È evidente che:

Per $h < h_{2}$ , si avranno $E > E_{2}$
Per $h > h_{2}$ , si avranno $E < E_{2}$

Si lascia trascorrere un altro intervallo di tempo $Δ t$ fino ad arrivare all'istante $t_{3} = 2 Δ t$ .

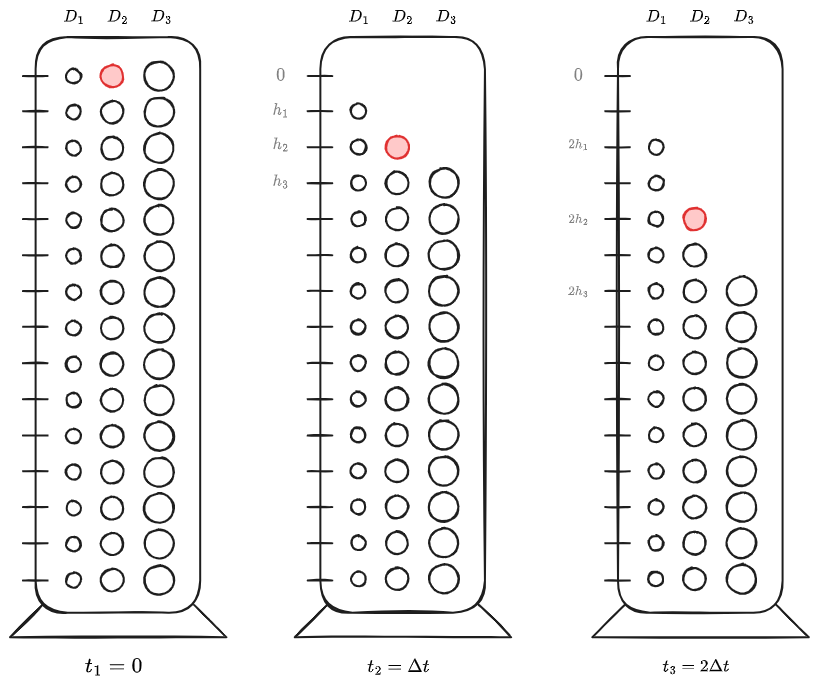
A questo punto notiamo che tutte le profondità sono raddoppiate:

Ogni particella $D_{1}$ si sposta a $2 h_{1}$ (1 posizione)
Ogni particella $D_{2}$ si sposta a $2 h_{2}$ (2 posizioni)
Ogni particella $D_{3}$ si sposta a $2 h_{3}$ (3 posizioni)

Pertanto sarà ancora, alla profondità $2 h_{2}$ , #Efficienza di rimozione $E = E_{2}$ . Si avranno ancora efficienze minori a quote maggiori ed efficienze maggiori a quote minori.

È evidente che le stesse considerazioni possano essere fatte per tutti i successivi istanti di tempo: $3 Δ t, 4 Δ t, 5 Δ t, . . .$

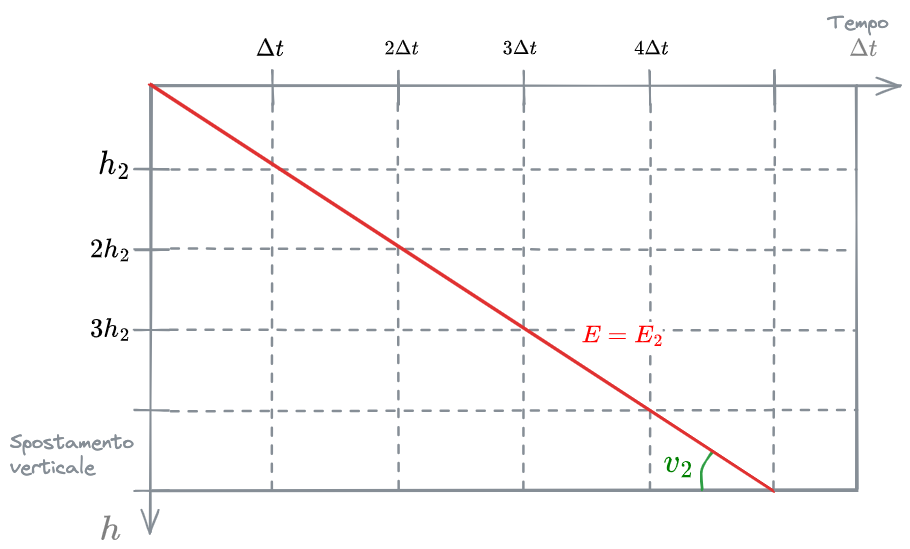
Si considera ora il piano profondità-tempo e si graficano i punti con la stessa #Efficienza di rimozione. La curva che unisce tali punti non può che essere una retta.
Per come è costruita la retta inoltre, si può affermare che la sua pendenza sia proprio la #velocità di sedimentazione.

[?] Perché è così? Spiega il paragrafo precedente

Si esaminano ora curve con diversa efficienza di rimozione. È evidente che a diametri maggiori ( $D_{3}$ ) saranno associati valori di efficienza minori.
Quindi le rette che rappresentano valori di efficienza $E < E_{2}$ hanno pendenze minori di $v_{2}$ : $v > v_{2}$ .
Analogamente, le rette rappresentanti $E > E_{2}$ , avranno $v < v_{2}$ .

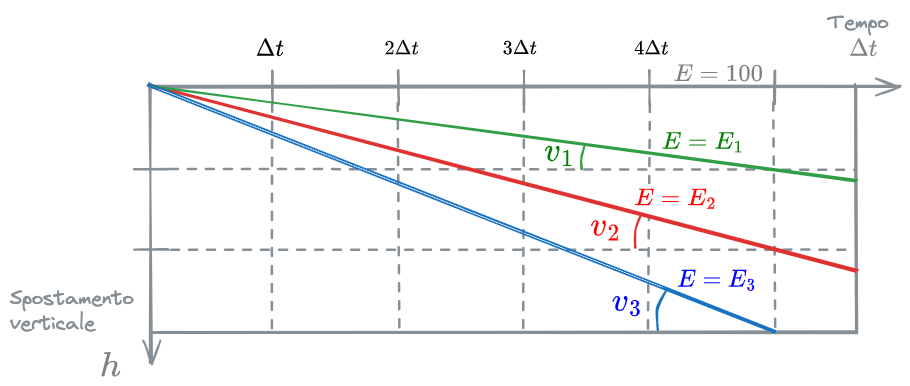
La prima grande conclusione di tutto ciò è che:

Ogni retta uscente dall'origine sul piano profondità-tempo rappresenta una curva a uguale valore di #Efficienza di rimozione.

In definitiva, se si guarda al piano profondità-tempo, ogni punto della retta a #Efficienza di rimozione $E = E_{2}$ , sarà un punto in cui sono state rimosse tutte le particelle con diametro $D > D_{2}$ . La percentuale di particelle con $D > D_{2}$ può d'altronde essere desunta dalla #Curva di Distribuzione Dimensionale - CDD o dalla #Curva Velocità di Sedimentazione - CVS.

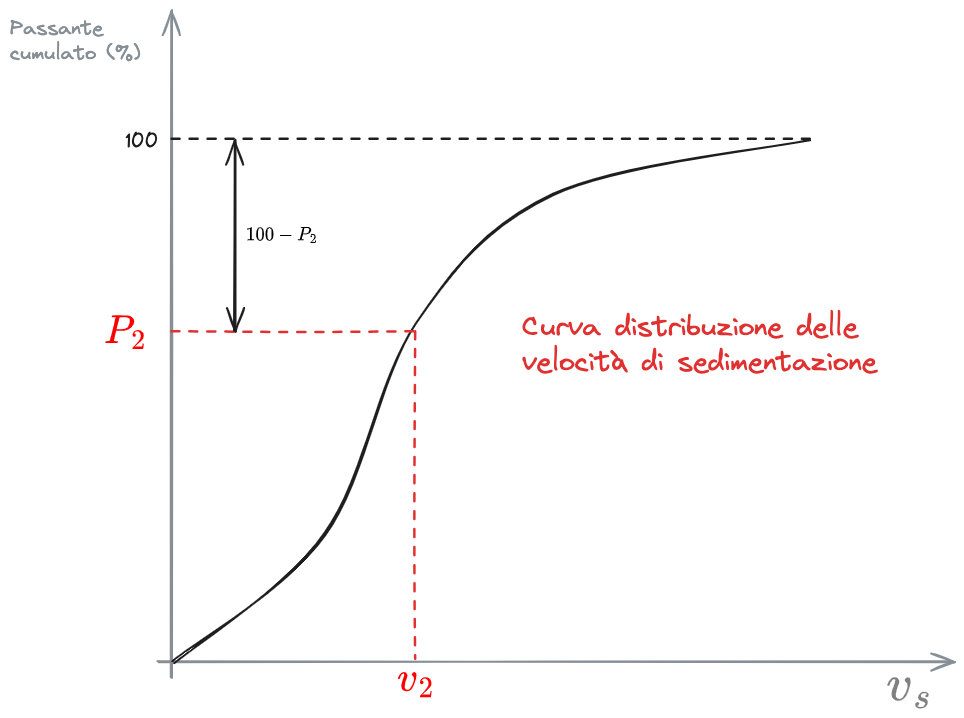
In riferimento alla CVS, la percentuale di particelle il cui diametro è $D > D_{2}$ è pari a $100 - P_{2}$ , che sarà anche l'#Efficienza di rimozione $E_{2}$ :

E_{2} = 100 - p_{2}

Si può quindi affermare che $E_{2}$ rappresenta la percentuale di particelle con velocità di sedimentazione maggiore a $v_{2}$ .

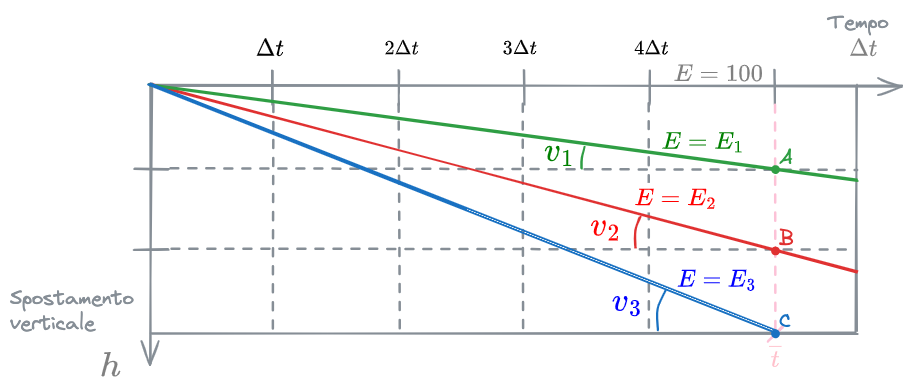
Si guardi ora all'istante $t = \overset{―}{t}$ .
A tale istante, le particelle $D_{1}$ saranno state rimosse completamente solo per quote inferiori a quelle corrispondenti al punto A; le particelle $D_{2}$ saranno state rimosse completamente solo per quote inferiori a quella corrispondente al punto B.
Le particelle $D_{3}$ risultano invece totalmente rimosse dalla colonna di sedimentazione.

Pertanto, fissato un istante di tempo $t = θ_{H}$ , risulta automaticamente determinata la retta a uguale #Efficienza di rimozione che incontra l'asse delle ascisse in quell'istante. Fissato un istante è quindi determinata la frazione di particelle che vengono completamente rimosse dalla colonna.

La velocità di sedimentazione che discrimina tra particelle completamente rimosse e non, può essere riguardata come #Velocità di Over-Flow: $v_{O R}$ .

In questo caso specifico, $v_{O R} = v_{3}$ .
Quindi, fissato un istante $t = θ_{H}$ risulta univocamente determinata la velocità di over-flow.

È evidente che a $t = θ_{H}$ , la percentuale complessiva di particelle rimosse dalla colonna risulterà superiore a $E = E_{3} = E (θ_{H})$ in quanto si dovrà tenere conto anche delle particelle con velocità di sedimentazione $v < v_{O R}$ che vengono rimosse parzialmente dalla colonna di sedimentazione.

Occorre definire un'#Efficienza globale di rimozione:

[?] Chiedere a qualcuno il grafico delle efficienze di rimozione nel caso di colonna di sedimentazione.
- [?] Perché a una efficienza di rimozione $E_{i}$ è associato un diametro $D_{i}$ (ammesso che sia vero)? Oppure, perché la pendenza di $E$ è proprio la velocità di sedimentazione di una particella?

Efficienza globale di rimozione

Come abbiamo visto in #Descrizione sperimentale della sedimentazione libera, individuata la velocità di Over-flow per una colonna di sedimentazione, a cui corrisponderà #Efficienza di rimozione pari a $E (θ_{H})$ per quelle particelle di diametro tale per cui hanno velocità di sedimentazione $v = v_{O R}$ , siamo interessati ancora a conoscere la percentuale di particelle complessiva che viene rimossa dalla colonna contando anche le particelle di diametro che non viene rimosso completamente.

Efficienza globale di rimozione???? ✅ 2024-01-29

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

efficienza globale di rimozione

$E = E (θ_{H}) + \sum_{i = 1}^{N} (E_{i} - E_{i + 1}) \frac{Δ h_{i}}{H}$

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

AUDIO DI Sara Maimone:
Efficienza è quello che tu elimini effettivamente.
Prendi E_5 che cade a $θ_{H}$ - analogo a quello di velocità di over flow nel caso non sperimentale. Particelle più piccole ad altezze limite per particelle più piccole vengono rimosse con un certo rapporto di rimozione e quindi lo devo sommare. Questo rapporto di rimozione è sempre il rapporto delle altezze, da sommare all'efficienza di rimozione.
La totale sarà, E5 di theta_H, + le intermedie per i rapporti di rimozione.

Sedimentazione per Flocculazione

sedimentazione per flocculazione (tipo 2)

La Sedimentazione per Flocculazione si ha quando le particelle solide durante il processo di sedimentazione tendono ad aggregarsi in particelle più grandi. Come conseguenza di ciò, la loro velocità di sedimentazione crescerà durante il processo.

I processi di sedimentazione per flocculazione sono estremamente difficili da modellare analiticamente, per cui si tende a studiarli esclusivamente per via sperimentale. Con riferimento alla #Descrizione sperimentale della sedimentazione libera, si procede a tracciare le curve a pari [[#Efficienza di rimozione]] nel caso in cui si verifichi sedimentazione per flocculazione.

Si nota immediatamente, come è ovvio che sia, che le curve non sono più delle rette, rispecchiando il fatto che la velocità di sedimentazione - e quindi la pendenza della curva - non sia più costante.

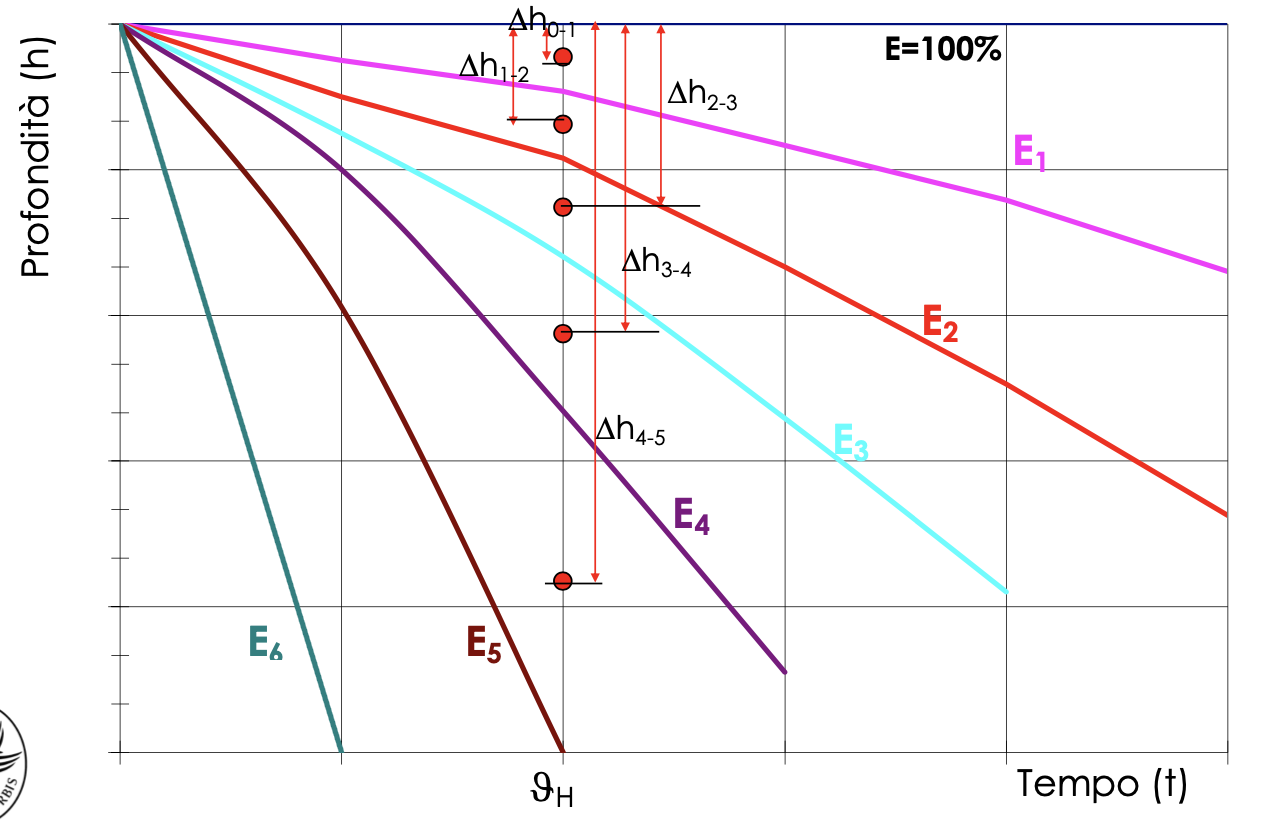
Anche in questo caso, fissato un tempo $t = θ_{H}$ è possibile individuare la curva a uguale efficienza di rimozione che interseca l'asse delle ascisse. Questa intersecherà l'asse con una certa pendenza $v_{O R}$ che può essere riguardata come l'analoga a una #Velocità di Over-Flow.

Si definisce così l'#Efficienza globale di rimozione come:

E = E (θ_{H}) + \sum_{i = 1}^{N} (E_{i} - E_{i + 1}) \frac{Δ h_{i}}{H}

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

Sedimentazione a zone

(sedimentazone)

sedimentazione ostacolata o a zone

La sedimentazione ostacolata o a zone si verifica quando si ha una concentrazione di particelle - [[Solidi Sospesi]] - elevata ( $C_{S S T} > 500 \frac{m g}{l}$ ) tale che le mutue distanze risultano dello stesso ordine di grandezza delle loro dimensioni.

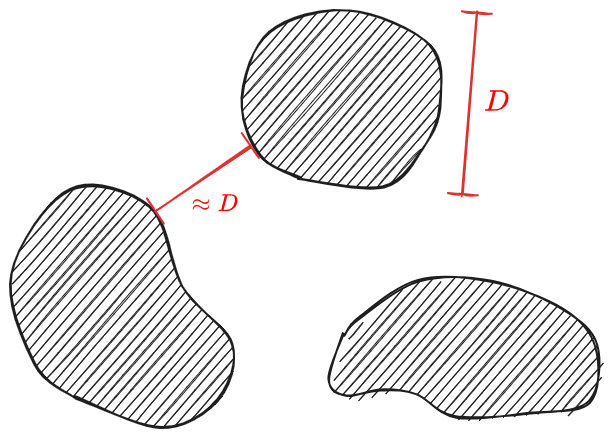
La trattazione analitica di questo tipo di sedimentazione è estremamente complessa e difficilmente percorribile. Un approccio teorico che conserva nel contempo rigore analitico e semplicità di interpretazione è dovuto a Kynch: #Teoria di Kynch

Teoria di Kynch

Si immagina di descrivere il processo di sedimentazione che avviene all'interno di una colonna di sedimentazione che può essere vista come un reattore di batch.

Si può ragionevolmente assumere, per "elevati" valori di concentrazione, che la velocità di sedimentazione $v$ della generica particella sia funzione esclusivamente della concentrazione $C$ di particelle nell'intorno di quella considerata.

Si assume inoltre che la concentrazione sia costante lungo la generica sezione orizzontale della colonna di sedimentazione.

Poiché le particelle si ostacolano a vicenda, queste si comportano come se fossero un blocco unico andando a formare un cosiddetto SCHELETRO SOLIDO. Questo tende a sedimentare come un tutt'uno e assume una certa velocità di sedimentazione detta $v_{s z}$ .
Rimanendo le distanze tra le particelle pressapoco costanti, anche la concentrazione rimarrà invariata durante il processo di sedimentazione.

osservazione

Nella #Sedimentazione a zone non ha senso considerare la distribuzione granulometrica delle particelle perché queste sedimentano alla stessa velocità di sedimentazione indipendentemente dalle loro dimensioni.

Osserviamo ora un processo di sedimentazione nelle condizioni appena descritte:

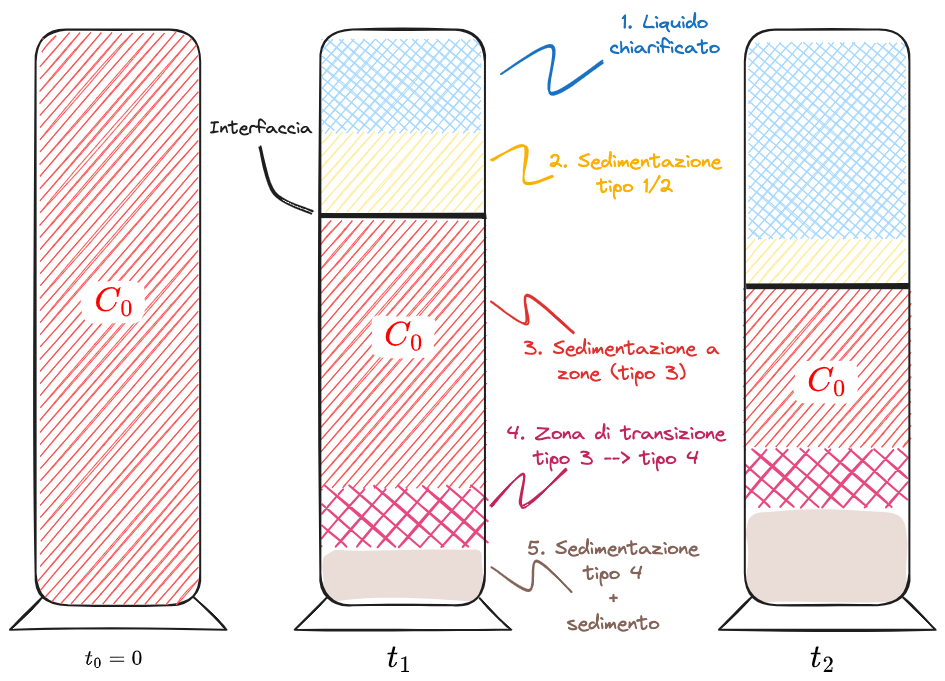
Dopo un certo intervallo di tempo, nella colonna si noterà la formazione di un'interfaccia di separazione netta fra un liquido quasi chiarificato (nel quale avviene #Sedimentazione libera o #Sedimentazione per Flocculazione) e una zona (3) in cui avviene #Sedimentazione a zone. Tale interfaccia è chiaramente visibile ad occhio nudo.

Lo scheletro solido si muove indisturbato verso il basso. A un certo punto, le particelle dello scheletro solido iniziano ad accumularsi sul fondo, comprimendo quelle già presenti. In questa zona della colonna (5) si avrà pertanto #Sedimentazione per Compressione.

Passato un sufficiente tempo, la zona 2 non sarà più presente e si passerà direttamente ad un'interfaccia che separa liquido chiarificato da una zona a sedimentazione di tipo 3. La zona 3 tende inoltre ad assottigliarsi a favore della zona 5.
Alla fine del processo ci ritroveremo in una condizione in cui la zona 3 è talmente sottile da rappresentare essa stessa l'interfaccia tra la 1 (liquido chiarificato) e la zona (5) di sedimentazione di tipo 4. A questo punto si ha esclusivamente #Sedimentazione per Compressione

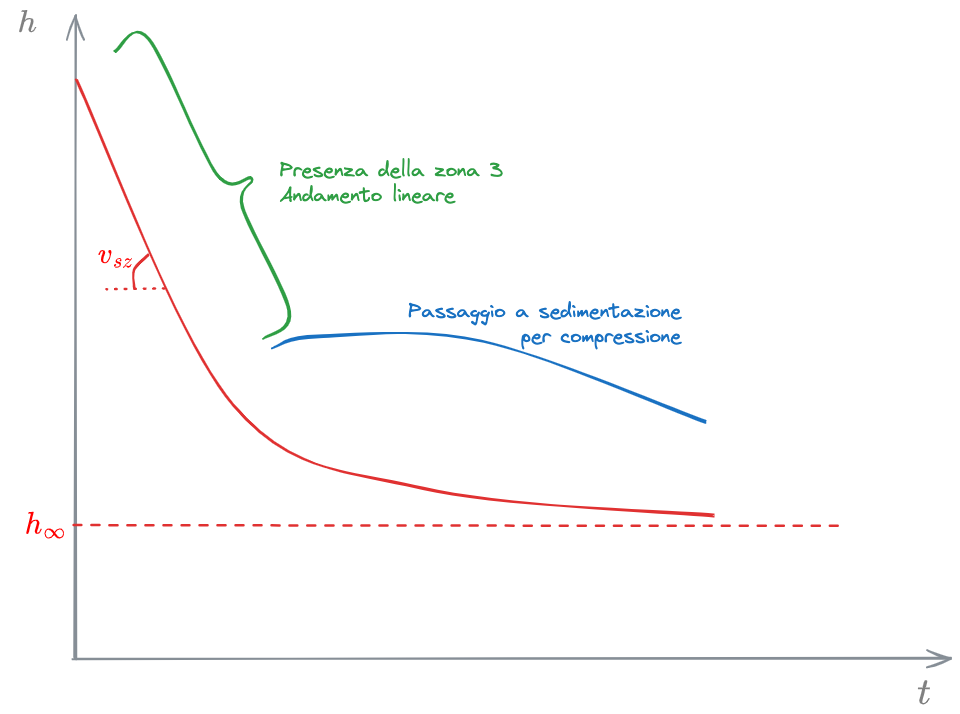
Le evidenze sperimentali ci mostrano che la velocità di sedimentazione, fin quando è presente la zona 3, è pari a $v_{s z}$ . Quando questa scompare del tutto, la velocità di sedimentazione decresce progressivamente fino ad annullarsi. Si ottiene un valore asintotico sul piano profondità-tempo pari a $h_{\infty}$ , che rappresenta lo spessore dello strato di fango oltre il quale non è ulteriormente compattabile sotto l'effetto del proprio peso.

Per diversi valori di concentrazione iniziale, ad esempio per $C_{1} > C_{0}$ , is avrebbe pendenza della curva nel tratto lineare minore, cioè avremmo minore velocità di sedimentazione.

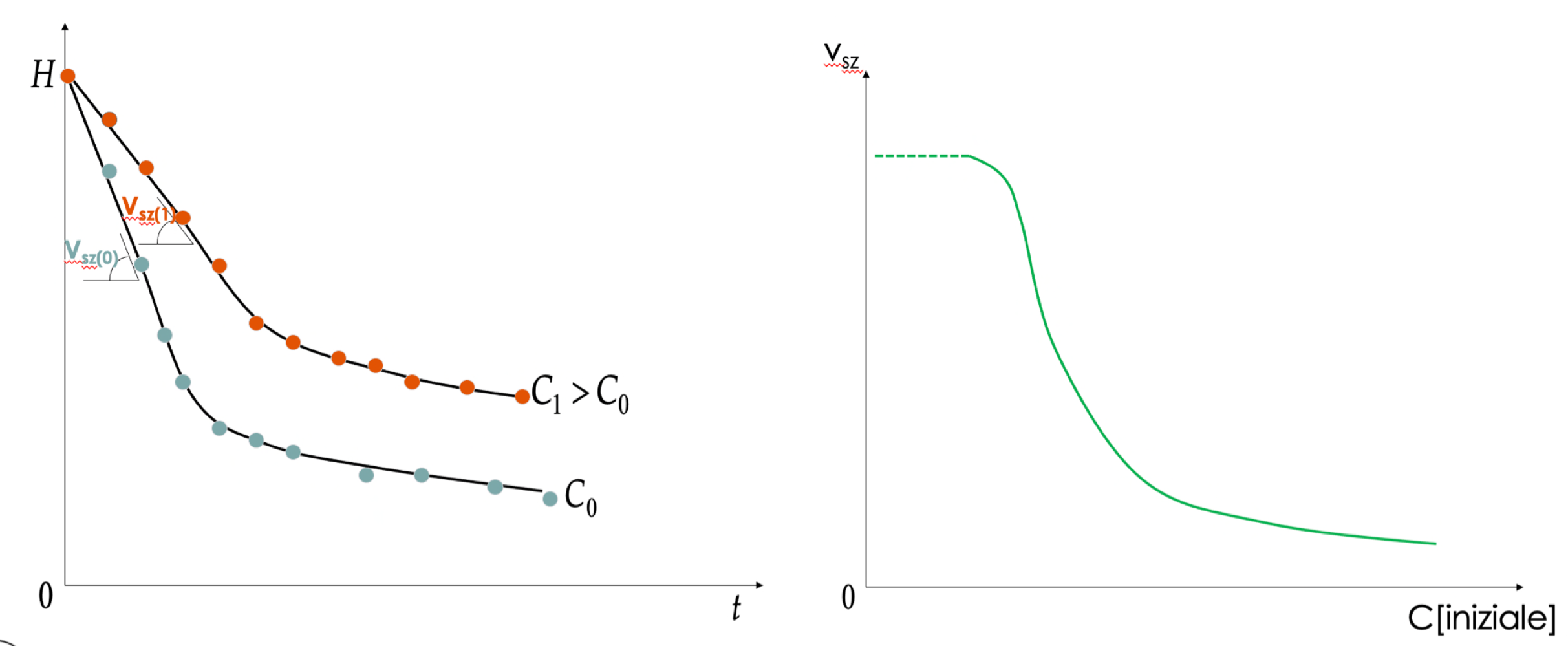
Tale effetto si verifica perché l'aumento della concentrazione delle particelle amplifica l'effetto delle interazione tra di esse: si ostacoleranno maggiormente il che si traduce in una minore velocità di sedimentazione.

Inoltre, anche il valore dello spessore limite tende ad aumentare: a parità di volume totale, a concentrazione iniziale maggiore ci saranno più particelle che una volta compresse occuperanno più spazio.

Si raffigura l'andamento della velocità di sedimentazione a zone ( $v_{s z}$ ) che si ottiene per vari valori di concentrazione iniziale:

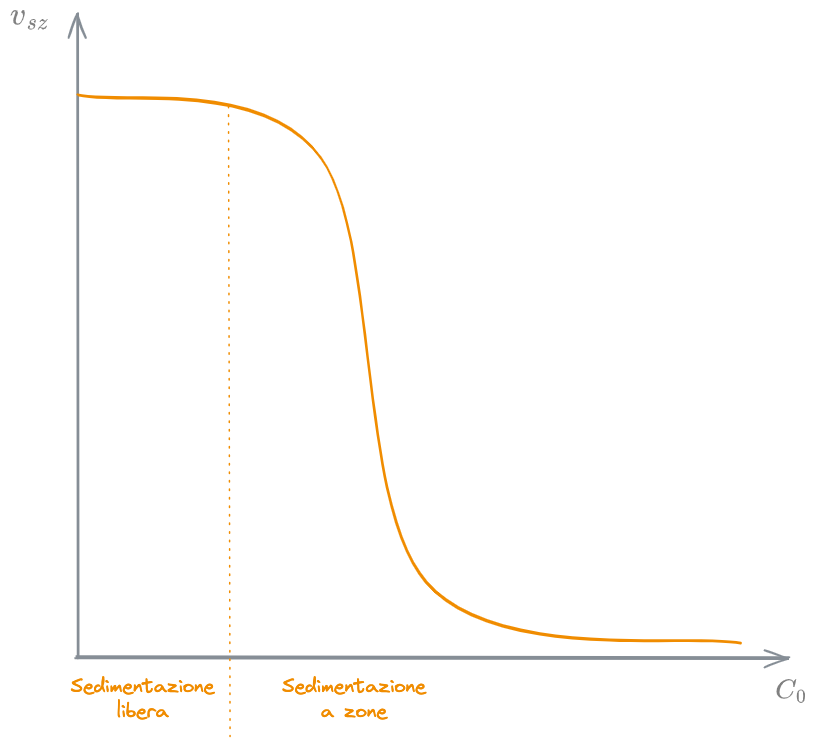
Per bassissimi livelli di $C_{0}$ , la velocità di sedimentazione tende a rimanere costante. I fenomeni di interferenza tra le particelle sono irrilevanti e si hanno processi di sedimentazione simili alla #Sedimentazione libera.

Oltre un certo valore di $C_{0}$ , la velocità di sedimentazione risente fortemente della concentrazione e si ha [[#Sedimentazione a zone]].

Sedimentazione per Compressione

sedimentazione per compressione (tipo 4)

La sedimentazione per compressione (tipo 4) avviene per l'effetto di ispessimento dovuto alla stratificazione dei solidi sul fondo della colonna di sedimentazione.

In tal caso si osserva un vero e proprio processo di consolidazione meccanico per espulsione di acqua con conseguente riduzione di volume.

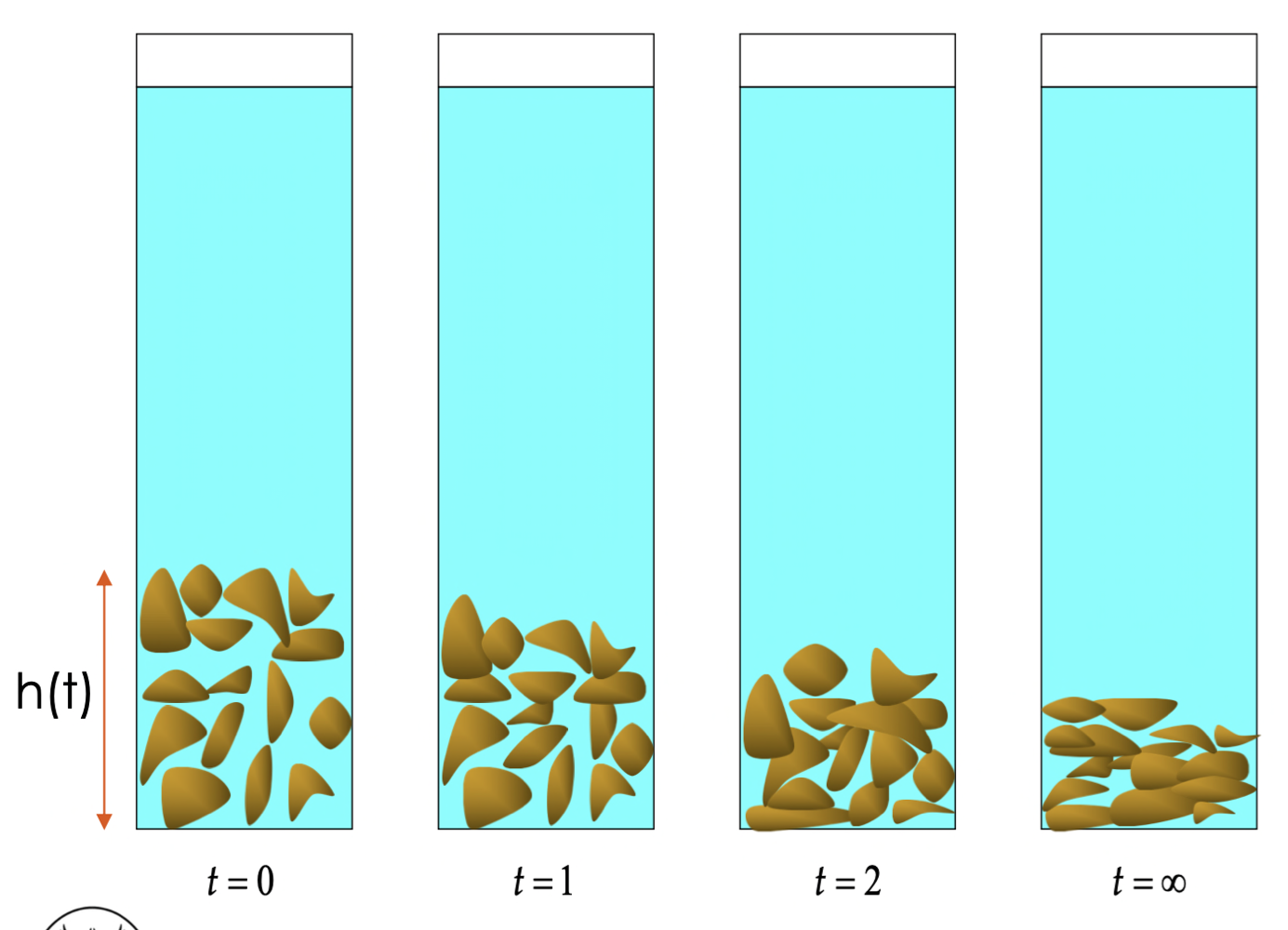
Si può assumere che la variazione di volume $d V$ sia proporzionale, secondo un coefficiente $k$ , alla differenza tra il volume $V$ occupato al generico istante $t$ e il volume $V_{\infty}$ che occuperanno i solidi al tempo $t = \infty$ :

$k$ dipende dalle caratteristiche delle particelle solide. Tiene conto di:

Interazione particelle con il liquido
Grado di agitazione del fango
Forze elettrostatiche delle particelle d'acqua

Essendo all'interno della colonna di sedimentazione la variazione di volume $d V$ univocamente identificata dalla variazione di altezza $d h$ si potrà scrivere:

\frac{d h}{d t} = - k (h - h_{\infty})

Integrando per separazione di variabili tra gli istanti $t = t_{0}$ e $t$ con i rispettivi spessori $h_{0}$ e $h$ , si ottiene:

\ln (\frac{h - h_{0}}{h_{0} - h_{\infty}}) = - k (t - t_{0})

La [[#Sedimentazione per Compressione]] si verifica proncipalmetne nelle vasche di trattamento dei fanghi derivati da altri processi di trattamento delle acque.

Si ottiene nelle cosiddette [[Vasche di ispessimento]]:

Vasche di sedimentazione con tempi di residenza molto elevati ( $θ_{H} \approx 24 h$ ).

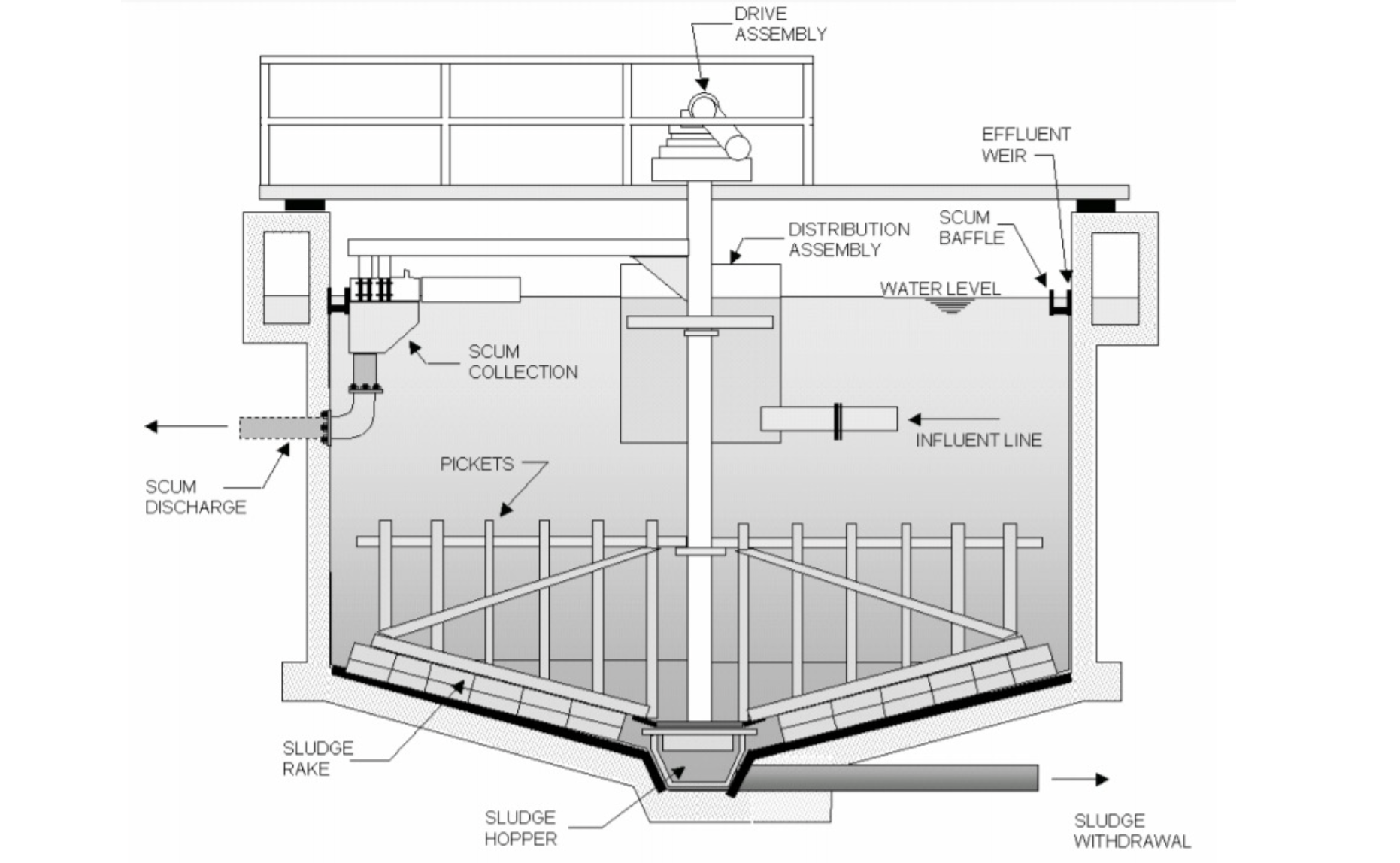
Alla base delle vasche di ispessimento sono presenti dei picchetti. La loro funzione è quella di vincere i deboli legami che ci sono tra le molecole polari di acqua ( $H_{2} O$ ) e le particelle di solido.