03. Reattori Ideali

3. Reattori a Flusso Continuo Ideali

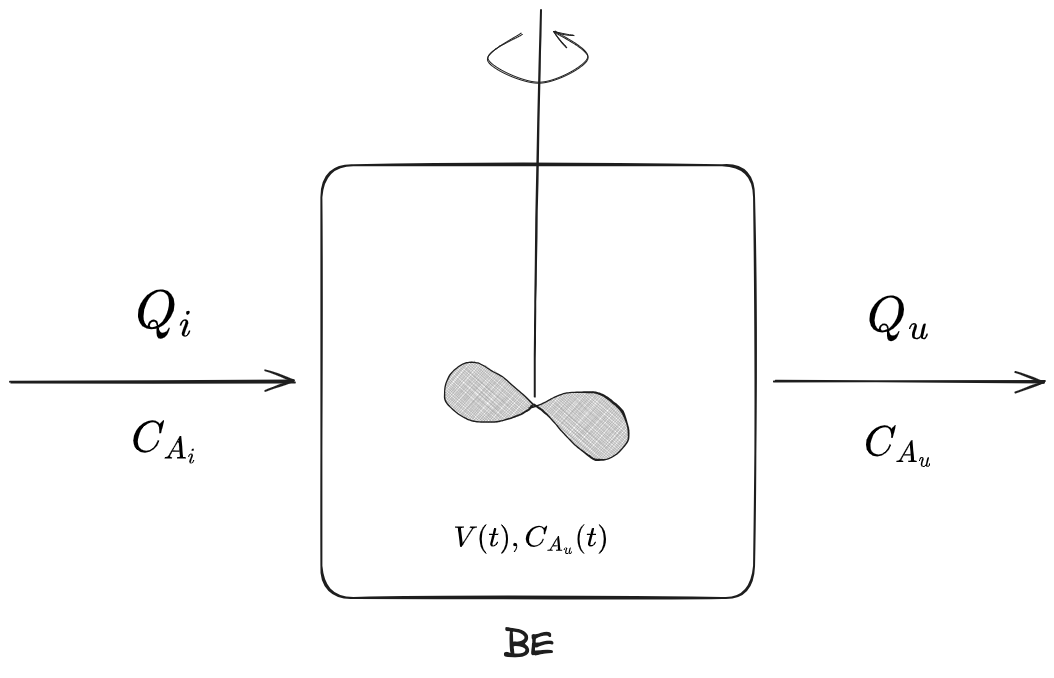
Si tratta di reattori che hanno un flusso di materia (portata in volume) continuo $Q_{i} (t)$ in ingresso a una data concentrazione $C_{A_{i}} (t)$ schematizzato come segue:

Quando si progetta un sistema si conosce/impone una tra:

Dati in ingresso
Portata di volume in uscita $Q_{u}$

Quindi o imponiamo $C_{A_{u}}$ e troviamo le caratteristiche del sistema (volume) o viceversa.

Come è fatto il reattore dal punto di vista del fluido?
Va definita la tipologia del reattore. Sfruttiamo due casi ideali

#Reattore CFSTR - Continuous Flow Stirred Tank Reactor
#Reattore PFR - Plug Flow Reactor

In entrambi i casi posso immaginare di trovarmi in condizioni di stazionarietà idraulica: sono passati i transitori di riempimento o svuotamento. $Q_{i} = Q_{u} = Q$ .

osservazione

La portata in ingresso e in uscita è la stessa, ma può comunque continuare a variare nel tempo.

Abbiamo interesse a comprendere come il reattore si comporta nella rimozione della specie chimica in ingresso. Vogliamo pertanto effettuare un'[[#Analisi Stimolo-Risposta]]
Per questo sfrutteremo il principio di conservazione della massa.

Bilancio di materia

È dato un generico reattore

Termini coinvolti:

Massa alimentata al sistema (in ingresso)
Massa prelevata al sistema (in uscita)
Reazione chimica (massa prodotta o consumata per effetto della reazione)
Massa accumulata nel sistema

INGRESSO - USCITA \pm REAZIONE (\begin{matrix} R e a g e n t e \\ P r o d o t t o \end{matrix}) = ACCUMULO [\frac{M a s s a}{T e m p o}]

Per scrivere l'equazione di bilancio dobbiamo:

Definire il sistema e i suoi confini
Scegliere la specie su cui effettuare il bilancio
Identificare flussi in ingresso e in uscita
Identificare le reazioni coinvolte (cinetica)

Tempo di residenza idraulica

tempo di residenza idraulica ($\theta_{h}$)

Si definisce tempo di residenza idraulica la grandezza:
$θ_{H} = \frac{V}{Q} [\frac{v o l u m e}{\frac{v o l u m e}{t e m p o}} = t e m p o] = [\frac{l}{\frac{l}{s}}] = [s]$
Nel #Reattore PFR rappresenta in quanto tempo il fluido percorre una certa distanza $x$ all'interno del reattore (essendo il volume $x \cdot A$ ) dove $A$ è l'area della sezione.
Nel #Reattore CFSTR invece è una grandezza fittizia e statistica non potendone definire un vero e proprio significato fisico.

Analisi Stimolo-Risposta

Stimolo: $Q (t), C_{A} (t)$
Risposta: $C_{A_{u}} (t)$

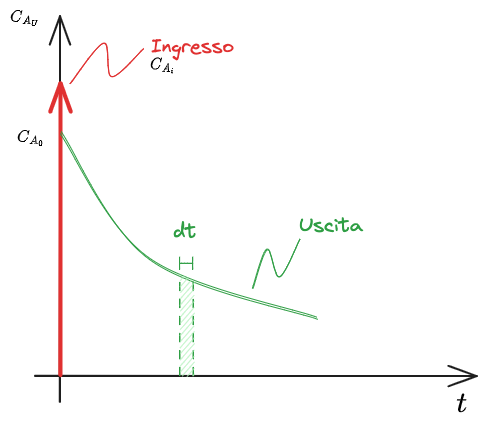
Segnali in ingresso

segnale in ingresso

L'andamento della concentrazione all'intgresso del reattore

Essendo l'analisi dei casi reali abbastanza complicata, optiamo per dei modelli ideali.
Introduciamo pertanto due tipi di segnali:

#Segnale a gradino
[[#Segnale a impulso]]
che descrivono l'andamento della $C_{A_{i}} (t)$ .

Segnale a gradino

Questo tipo di segnale passa da $0$ a $C_{A_{0}}$ al tempo $t = 0$ in modo repentino.
L'andamento analitico è descritto come segue:

C_{A_{0}} (t) = {\begin{cases} 0 & t \leq 0^{-} \\ C_{A_{0}} & t \geq 0^{+} \end{cases}

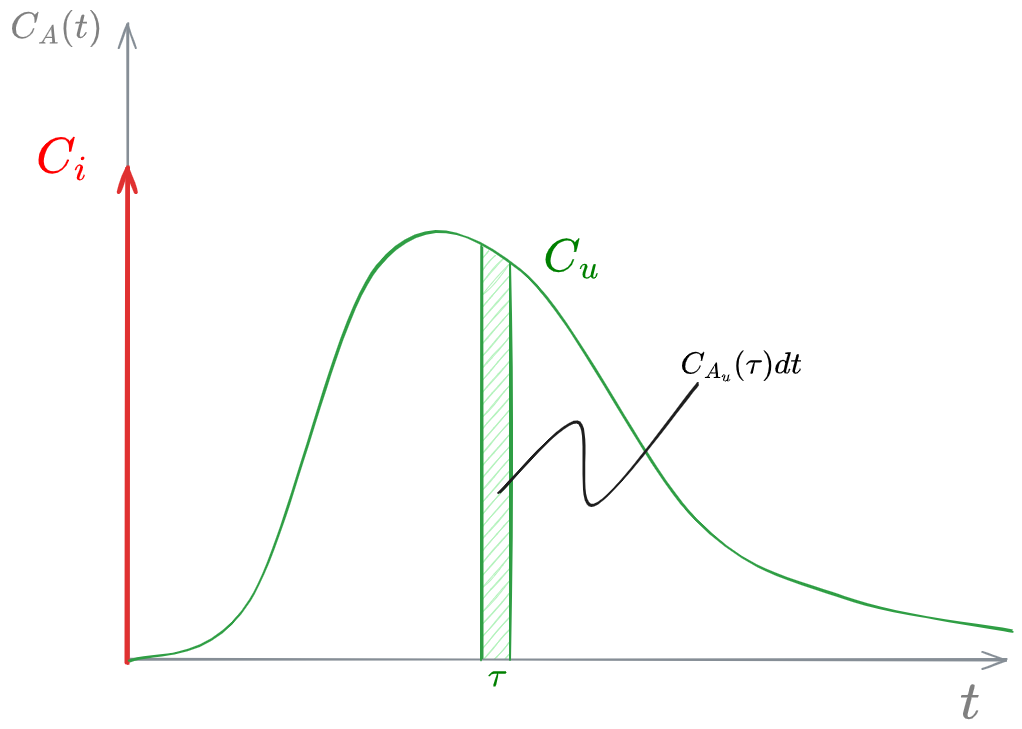
Segnale a impulso

%%🖋 Edit in Excalidraw, and the dark exported image%%

Questo tipo di segnale è invece definito in un unico punto, $t = 0$ e in questo istante ha valore infinito (indicato nel grafico con una freccia).

C_{A} (t) = {\begin{cases} 0 & t \neq 0 \\ \infty & t = 0 \end{cases}

L'andamento corrisponde a quello della $δ$ di Dirac.

Si può dimostrare che calcolando l'area sotto il grafico (facendo l'integrale della funzione) otteniamo un valore finito

\int_{- \infty}^{\infty} C_{A} (t) d t = F I N I T O

Vediamo che l'integrale corrisponde dimensionalmente a una concentrazione per un tempo. Moltiplicando per la portata, otteniamo la massa (in moli)

\begin{aligned} [] C o n c e n t r a z i o n e \times T e m p o] & = [\frac{m o l}{l} \times h] \times (P o r t a t a) \\ = [\frac{m o l}{l} \times h \times \frac{l}{h}] = [m o l] \end{aligned}

Reattore CFSTR

(Continuous Flow Stirred Tank Reactor - Reattore a miscelazione completa)

reattore cfstr

Il reattore CFSTR è un reattore basato sulle seguenti due ipotesi:

Il flusso in ingresso si disperde nel reattore istantaneamente
Il flusso in ingresso si disperde nel reattore uniformemente

Dove $i$ sta per ingresso e $u$ per uscita

Ci chiediamo subito quale sia la concentrazione $C_{A}$ all'interno del reattore.
Immaginiamo di prendere un punto in corrispondenza dell'uscita. Avrà concentrazione $C_{A_{u}}$ . Per l'ipotesi numero 2, essendo le condizioni all'interno del reattore uniformi, tutto il volume interno si troverà a concentrazione $C_{A} = C_{A_{u}}$ .

La concentrazione è affetta da tue fattori:

Idraulico: diluizione (istantanea per ipotesi 1)
Chimico: ciò che rende possibile che $C_{A_{u}} < C_{A_{i}}$
- Questa prende un certo tempo

[[2023-10-06]]
[[Alessandra Polettini]]
![[Recording 20231006143728.webm]]
%%

Bilancio di materia - CFSTR

Vediamo il #Reattore CFSTR.

Possiamo trovare una portata in massa (moli) moltiplicando la portata in volume con la concentrazione
Rispetto a

INGRESSO - USCITA \pm REAZIONE (\begin{matrix} R e a g e n t e \\ P r o d o t t o \end{matrix}) = ACCUMULO [\frac{M a s s a}{T e m p o}]

Possiamo quindi scrivere

Q C_{A_{i}} - Q C_{A_{u}} \pm r_{A} V = \frac{d M_{A}}{d t}

dove:

M_{A} = C_{A_{u}} V

Quindi la derivata diventa:

\begin{aligned} \frac{d M_{A}}{d t} & = V \frac{d C_{A_{u}}}{d t} + C_{A_{u}} \frac{d V}{d t} = \\ = V \frac{d C_{A_{u}}}{d t} Se considero V costante \end{aligned}

L'equazione di bialancio in definitiva è

$Q C_{A_{i}} - Q C_{A_{u}} \pm r_{A} V = V \frac{d C_{A_{u}}}{d t}$

osservazione

Avevamo visto che la velocità di reazione in reazioni omogenee poteva essere espressa come
$r_{A} = \frac{d C_{A_{u}}}{d t}$
Che differenza c'è quindi tra $r_{A}$ e la derivata della concentrazione.
Osserviamo che la concentrazione nel reattore può variare per diversi motivi. Ad esempio può variare anche se variamo la concentrazione in ingresso.

$r_{a}$ conta solo la variazione di concentrazione dovuta alla reazione
La derivata conta tutte le altre variazioni

Introducendo il #Tempo di residenza idraulica $θ_{H}$ posso riscrivere il bilancio come:

\frac{C_{A_{i}}}{θ_{H}} - \frac{C_{A_{u}}}{θ_{H}} - r_{A} = \frac{d C_{A_{u}}}{d t}

Bilancio di materia stazionario - CFSTR

Supponendo di trovarci nel caso stazionario la concentrazione in uscita non varierà più pertanto del bilancio rimane:

\frac{C_{A_{i}}}{θ_{H}} - \frac{C_{A_{u}}}{θ_{H}} - r_{A} = 0

che conviene riscrivere raccogliendo $\frac{1}{θ_{H}}$

$\frac{C_{A_{i}} - C_{A_{u}} - θ_{H} r_{A}}{θ_{H}} = 0$

Volendo possiamo da questa ricavare il #Tempo di residenza idraulica $θ_{H}$ :

θ_{H} = - \frac{1}{r_{A}} (C_{A_{0}} - C_{A_{u}})

Segnale a gradino - CFSTR

Possiamo guardare vari casi:

[[#1 - Specie tracciante - CFSTR]]
[[#2 - Cinetica di ordine 0 - CFSTR]]
[[#3 - Cinetica di ordine 1 - CFSTR]]
[[#4 - Cinetica di ordine 2 - CFSTR]]
[[#5 - Cinetica di saturazione - CFSTR]]

1 - Specie tracciante - Gradino - CFSTR

Con specie tracciante ci si riferisce al caso in cui non avviene nessuna reazione, ovvero in cui

r_{A} = 0

Il [[#Bilancio di materia - CFSTR]] diventa

\begin{aligned} \frac{V d C_{A_{u}}}{d t} & = Q C_{A_{0}} - Q C_{A_{u}} + r_{A} V \\ Divido per V \\ \frac{d C_{A_{u}}}{d t} & = \frac{Q C_{A_{0}} - Q C_{A_{u}}}{V} \end{aligned}

Ricordando il #Tempo di residenza idraulica posso scrivere

\frac{d C_{A_{u}}}{d t} = \frac{C_{A_{0}} - C_{A_{u}}}{θ_{h}}

che posso integrare per separazione di variabili (occhio al cambio di segno):

\int_{0}^{C_{A_{u}} (t)} \frac{d C_{A_{u}}}{C_{A_{u}} - C_{A_{0}}} = - \int_{0}^{t} \frac{d t}{θ_{H}}

Ottenendo

\begin{array}{r} {\ln (C_{A_{u}} - C_{A_{0}}) |}_{0}^{C_{A_{u} (t)}} = - {\frac{1}{θ_{H}} t |}_{0}^{t} \\ \ln \frac{C_{A_{u} (t)} - C_{A_{0}}}{- C_{A_{0}}} = - \frac{t}{θ_{H}} \end{array}

che in definitiva diventa:

$C_{A_{u}} (t) = C_{A_{0}} (1 - e^{- \frac{t}{θ_{H}}})$

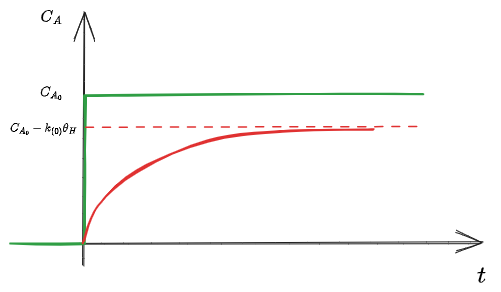
Vediamo quindi che:

Il segnale a gradino è trasformato in una risposta continua dal reattore
- Questo è dovuto alla miscelazione
$C_{A_{0}}$ in uscita si ottiene solo come asintoto. Non si ottiene mai perfettamente

All'atto pratico, posso dire che oltre una certa $C_{A_{u}} (t)$ mi trovo in condizioni stazionarie.
Posso scegliere arbitrariamente il limite.
Dico che, se $C_{A_{u}} (t) = 95 % C_{A_{0}}$ ho raggiunto lo stato stazionario.

Definisco quindi un tempo di stato stazionario come il tempo $t_{s t}$ necessario a raggiungere la concentrazione detta prima.

\begin{aligned} 95 % C_{A_{0}} & = C_{A_{0}} (1 - e^{- \frac{t_{s t}}{θ_{H}}}) \\ e^{- \frac{t_{s t}}{θ_{H}}} & = 1 - 0.95 = 0.05 \end{aligned}

e quindi

⟹ t_{s t} = - \ln (0.05) \cdot θ_{H} \approx 3 θ_{H}

$t_{s t} \approx 3 θ_{H}$

2 - Cinetica di ordine 0 - Gradino - CFSTR

Vediamo la risposta di un [[#Reattore CFSTR]] a un [[#Segnale a gradino]].
A partire dal [[#Bilancio di materia - CFSTR]], tenendo a mente che $r_{A} = - k_{(0)}$

\begin{aligned} \frac{V d C_{A_{u}}}{d t} & = Q C_{A_{0}} - Q C_{A_{u}} + r_{A} V \\ Divido per V \\ \frac{d C_{A_{u}}}{d t} & = \frac{Q C_{A_{0}} - Q C_{A_{u}} - k_{(0)}}{V} \\ \frac{d C_{A_{u}}}{d t} & = \frac{C_{A_{0}} - C_{A_{u}} - k_{(0)} θ_{H}}{θ_{H}} = \frac{(C_{A_{0}} - k_{(0)} θ_{H}) - C_{A_{u}}}{θ_{H}} \end{aligned}

che può essere integrata per separazione di variabili

\int_{0}^{C_{A_{u}} (t)} \frac{d C_{A_{u}}}{C_{A_{u}} - (C_{A_{0}} - k_{(0)} θ_{H})} = - \int_{0}^{t} \frac{d t}{θ_{H}}

ottenendo:

\ln (\frac{C_{A_{u}} (t) - (C_{A_{0}} - k_{(0)} θ_{H})}{- (C_{A_{0}} - k_{(0)} θ_{H})}) = - \frac{t}{θ_{H}}

da cui, risolvendo per $C_{A_{u}}$ :

$C_{A_{u}} (t) = (C_{A_{0}} - k_{(0)} θ_{H}) (1 - e^{- \frac{t}{θ_{H}}})$
Cinetica ord 0 - segnale a gradino - CFSTR - 03. Reattori Ideali 2023-10-24 11.46.03.excalidraw.png

Procedendo in modo del tutto analogo a [[#1 - Specie tracciante - CFSTR]] abbiamo

0.95 (C_{A_{0}} - k_{(0)} θ_{H}) = (C_{A_{0}} - k_{(0)} θ_{H}) (1 - e^{- \frac{t_{s t}}{θ_{H}}})

da cui otteniamo:

$t_{s t} = 3 θ_{H}$

proprio come nel caso precedente.

3 - Cinetica di ordine 1 - Gradino - CFSTR

C_{A} (t) = \frac{C_{A_{0}}}{1 + k_{(1)} θ_{H}} (1 - e^{- \frac{1 + k_{(1)} θ_{H}}{θ_{H}} t})

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

4 - Cinetica di ordine 2 - Gradino - CFSTR

5 - Cinetica di saturazione - Gradino - CFSTR

Segnale a impulso - CFSTR

Per caratterizzare meglio il comportamento di un [[#Reattore CFSTR]] è utile studiare la sua risposta anche a un [[#Segnale a impulso]]. Si guarderà solo al caso di specie tracciante ( $r_{A} = 0$ ).

Dal bilancio di materia si ha che:

\frac{V d C_{A_{u}}}{d t} = Q C_{A_{i}} - Q C_{A_{u}} + r_{A} V

Ora però è lecito avere dei dubbi su come vada rappresentato il segnale in ingresso ( $C_{A_{i}}$ ). Posso procedere come segue:

Supporre che entra sempre $0 ⟹ C_{A_{i}} = 0$
Da qualche parte, rappresentare che, solo in quel preciso istante, sto facendo entrare una massa finita

Per via delle supposizioni appena fatte, l'equazione del bilancio di materia diventa semplicemente

\frac{V d C_{A_{u}}}{d t} = - Q C_{A_{u}}

la quale può essere integrata per separazioni di variabili

\int_{C_{A_{0}}}^{C_{A} (t)} \frac{d C_{A}}{C_{A_{u}}} = - \int_{0}^{t} \frac{d t}{θ_{H}}

La concentrazione dovuta al [[#Segnale a impulso]] sarà

C_{A_{0}} = \frac{M}{V}

dove $C_{A_{0}}$ non rappresenta più la concentrazione in ingresso al reattore, ma quella che si instaura al suo interno come conseguenza del segnale applicato.
Integrando l'equazione sopra, si ottiene:

C_{A_{u}} (t) = C_{A_{0}} e^{- \frac{t}{θ_{H}}}

Il cui andamento è rappresentato nel grafico che segue

%%🖋 Edit in Excalidraw, and the dark exported image%%

Calcoliamo ora la massa tracciante che esce dal reattore in un certo istante $t^{*}$ .
Questa massa sarà data dall'area del rettangolo in figura (a meno di un fattore $Q$ ).

M_{A_{u}} (t^{*}) = Q \cdot C_{A_{u}} (t^{*}) \cdot d t

dove $t^{*}$ è il punto medio dell'intervallo $d t$ .
Se quella è la massa che esce in quell'istante, è anche la massa che è rimasta nel reattore proprio per un tempo $t^{*}$ .

Funzione di distribuzione - CFSTR

Si vuole cercare la #Funzione di distribuzione dei tempi di residenza per un [[#Reattore CFSTR]].

E (t) = \frac{Massa di tracciante che ha avuto θ_{H} \sim t^{*}}{\int_{0}^{\infty} C_{u} (t) d t}

a meno delle portate $Q$ .

Nel caso di un [[#Segnale a impulso - CFSTR]] (ricordo di aver preso ad esempio il [[#Segnale a impulso]]), la risposta del reattore, $C_{u} (t)$ è

C_{A_{u}} (t) = C_{A_{0}} e^{- \frac{t}{θ_{H}}}

Integrando tra 0 e $\infty$ si ha:

\int_{0}^{\infty} C_{u} (t) d t = \int_{0}^{\infty} C_{A_{0}} e^{- \frac{t}{θ_{H}}} d t = C_{A_{0}} θ_{H}

La [[#Funzione di distribuzione dei tempi di residenza]] nel caso di un [[#Reattore CFSTR]] è quindi:

E (t) = \frac{C_{A_{0}} e^{- \frac{t}{θ_{H}}}}{C_{A_{0}} θ_{H}} = \frac{e^{- \frac{t}{θ_{H}}}}{θ_{H}}

[?] Perché la funzione di distribuzione è moltiplicata per $d θ_{H}$ ? Se è il rapporto tra la massa di tracciante con tempo di residenza paro a $t^{*}$ e la massa totale in ingresso, perché la moltiplico per un tempo?

Possiamo scrivere, ricordando quanto detto sulla funzione di distribuzione.

E (θ_{H}^{*}) d θ_{H} = \frac{Massa di tracciante che ha avuto θ_{H} \sim t^{*}}{M_{A_{0}}}

[?] Perché la funzione di distribuzione è moltiplicata per $d θ_{H}$ ? Se è il rapporto tra la massa di tracciante con tempo di residenza paro a $t^{*}$ e la massa totale in ingresso, perché la moltiplico per un tempo?

E (θ_{H}^{*}) d θ_{H} = \frac{C_{A_{u}} (t^{*}) d t}{\int_{0}^{\infty} C_{A_{u}} (t) d t}

Sostituendo a $C_{A_{u}}$ l'espressione

C_{A_{u}} (t) = C_{A_{0}} e^{- \frac{t}{θ_{H}}}

ottengo

E (t^{*}) d t = \frac{C_{A_{u}} (t^{*}) d t}{\int_{0}^{\infty} C_{A_{u}} (t) d t} = \frac{C_{A_{0}} e^{- \frac{t^{*}}{θ_{H}}}}{C_{A_{0}} θ_{H}}

che restituisce in definitiva

E (t) = \frac{e^{- \frac{t}{d θ_{H}}}}{θ_{H}}

che è l'andamento della funzione di distribuzione per un [[#Reattore CFSTR]].
%%

%%🖋 Edit in Excalidraw, and the dark exported image%%

Essendo l'andamento un'esponenziale decrescente, notiamo che ci sarà sempre una certa frazione di particelle che non escono mai dal reattore.

Inoltre è evidente che ogni particella abbia un valore di $θ_{H}$ differente.
Calcoliamo ora il valor medio di $θ_{H}$ : ${\overset{―}{θ}}_{H}$

{\overset{―}{θ}}_{H} = \int_{0}^{\infty} t E (t) d t = \int_{0}^{\infty} \frac{t e^{- \frac{t}{θ_{H}}}}{θ_{H}} d t \overset{(\dots)}{=} θ_{H} = \frac{V}{Q}

Reattore PFR

(Plug Flow Reactor)
Reattore con flusso a pistone

Il reattore PFR è un reattore basato sulle seguenti ipotesi:

Assenza di miscelazione in senso longitudinale
Miscelazione perfetta in senso trasversale

Immagino di introdurre nel reattore un certo volumetto di fluido (in rosso). Questo coll'avanzare del tempo si sposterà in avanti lo stesso accadrà ad altri volumetti che introduco successivamente:

Il fluido, entrando compie l'azione di un pistone.
Muovendoci verso valle del reattore, il fluido avrà concentrazione via via minore. Mi aspetto quindi di avere un gradiente continuo lungo il reattore.

Bilancio di materia - PFR

In questo caso la concentrazione varia da sezione a sezione. Per scrivere il bilancio, prendiamo in considerazione una porzione infinitesima $d V$ .

In questo caso notiamo che la concentrazione è quindi funzione sia dell'ascissa $x$ che del tempo $t$ .

Rispetto a

INGRESSO - USCITA \pm REAZIONE (\begin{matrix} R e a g e n t e \\ P r o d o t t o \end{matrix}) = ACCUMULO [\frac{M a s s a}{T e m p o}]

possiamo scrivere:

\begin{aligned} Q C_{A} (x, t) - Q C_{A} (x + d x, t) \pm r_{A} d V & = \frac{\partial C_{A} (x, t)}{\partial t} d V (Considero già V costante) \\ Sviluppo il termine di uscita & con Taylor al primo ordine \\ Q C_{A} (x, t) - Q (C_{A} (x, t) + \frac{\partial C_{A} (x, t)}{\partial x} d x) \pm r_{A} A d x & = \frac{\partial C_{A} (x, t)}{\partial t} d V \\ - \frac{Q}{A} \frac{\partial C_{A} (x, t)}{\partial x} d x \pm r_{a} A d x & = \frac{\partial C_{A} (x, t)}{\partial t} A d x \\ - \frac{\partial C_{A}}{(\frac{A \partial x}{Q})} \pm r_{A} = \frac{\partial C_{A}}{\partial t} \end{aligned}

dove riconosco il [[#Tempo di residenza idraulica]]:

\frac{A \partial x}{Q} = θ_{H}

Ottengo così l'equazione di [[#Bilancio di materia]] per il [[#Reattore PFR]]

\frac{\partial C_{A}}{\partial\theta_A} \pm r_{A} = \frac{\partial C_{A}}{\partial t}
$

Questa equazione può essere integrata per ottenere la $C_{A} (x, t)$ o $C_{A} (θ_{H} (x), t)$ .

Trattandosi di un'equazione differenziale alle derivate parziali, difficile quindi da risolvere analiticamente, guarderemo in parallelo a:

Andamento nel tempo, fissato $x$
Andamento in $x$ , fissato il tempo

Segnale a gradino - PFR

[[#1- Specie tracciante - PFR]]
[[#2 - Cinetica di ordine 0 - PFR]]
[[#3 - Cinetica di ordine 1 - PFR]]
[[#4 - Cinetica di ordine 2 - PFR]]
[[#5 - Cinetica di saturazione - PFR]]

1- Specie tracciante - Gradino - PFR

%%🖋 Edit in Excalidraw, and the dark exported image%%

Guardiamo diverse istantanee del reattore:

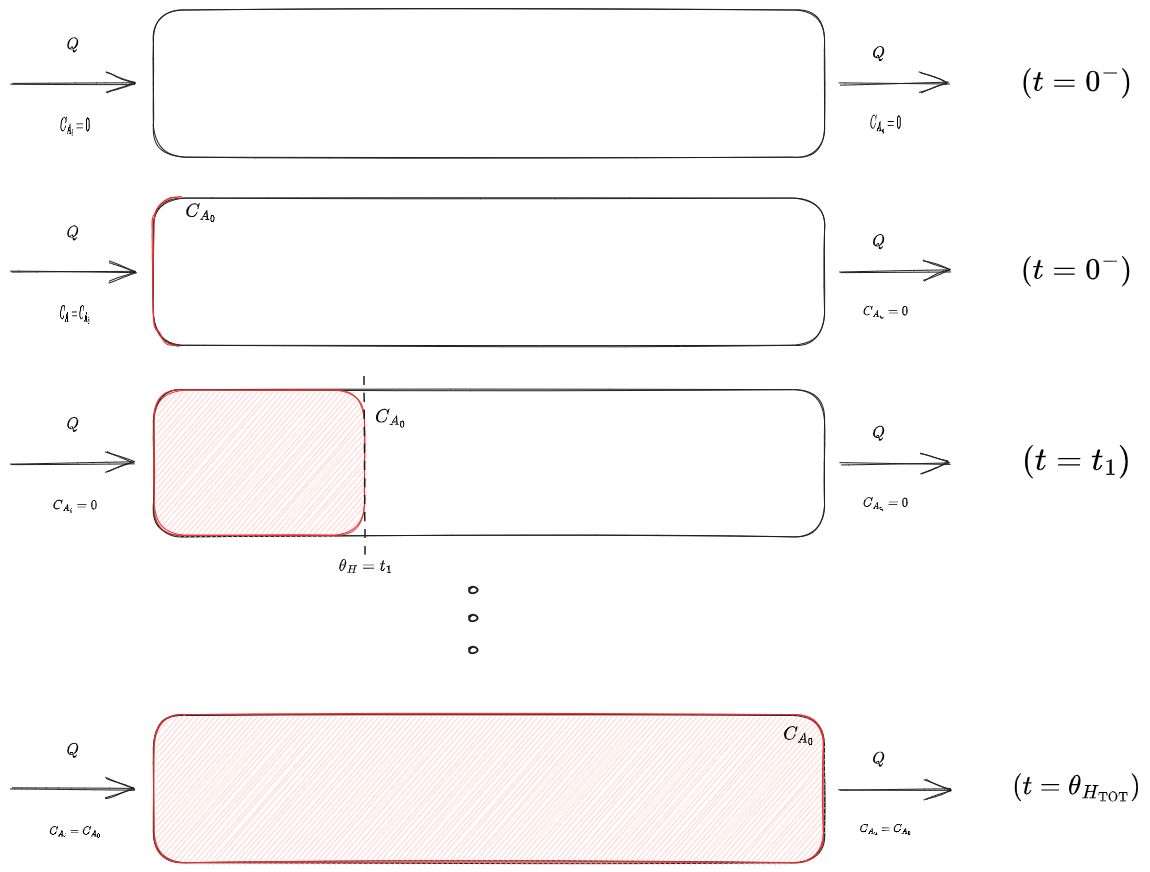
%%🖋 Edit in Excalidraw, and the dark exported image%%

Si fanno quindi 2 grafici:
La concentrazione in uscita $C_{A_{u}}$ in funzione del tempo $t$ e la concentrazione in funzione dell'ascissa rappresentata come $θ_{H}$ .

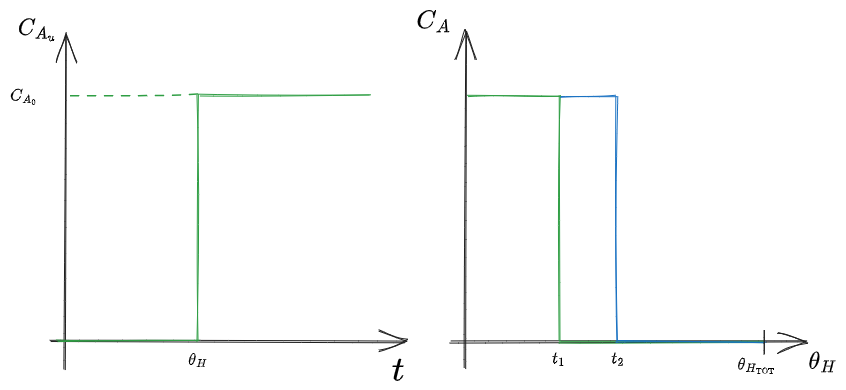
%%🖋 Edit in Excalidraw, and the dark exported image%%

osservazione

Il grafico a sx è uguale all'andamento generico del [[#Segnale a gradino]] ma sfasato nel tempo di $θ_{H}$ .

2 - Cinetica di ordine 0 - Gradino - PFR

Nel caso in cui nel reattore si verifichi una reazione di ordine $α$ l'andamento sarà leggermente diverso.

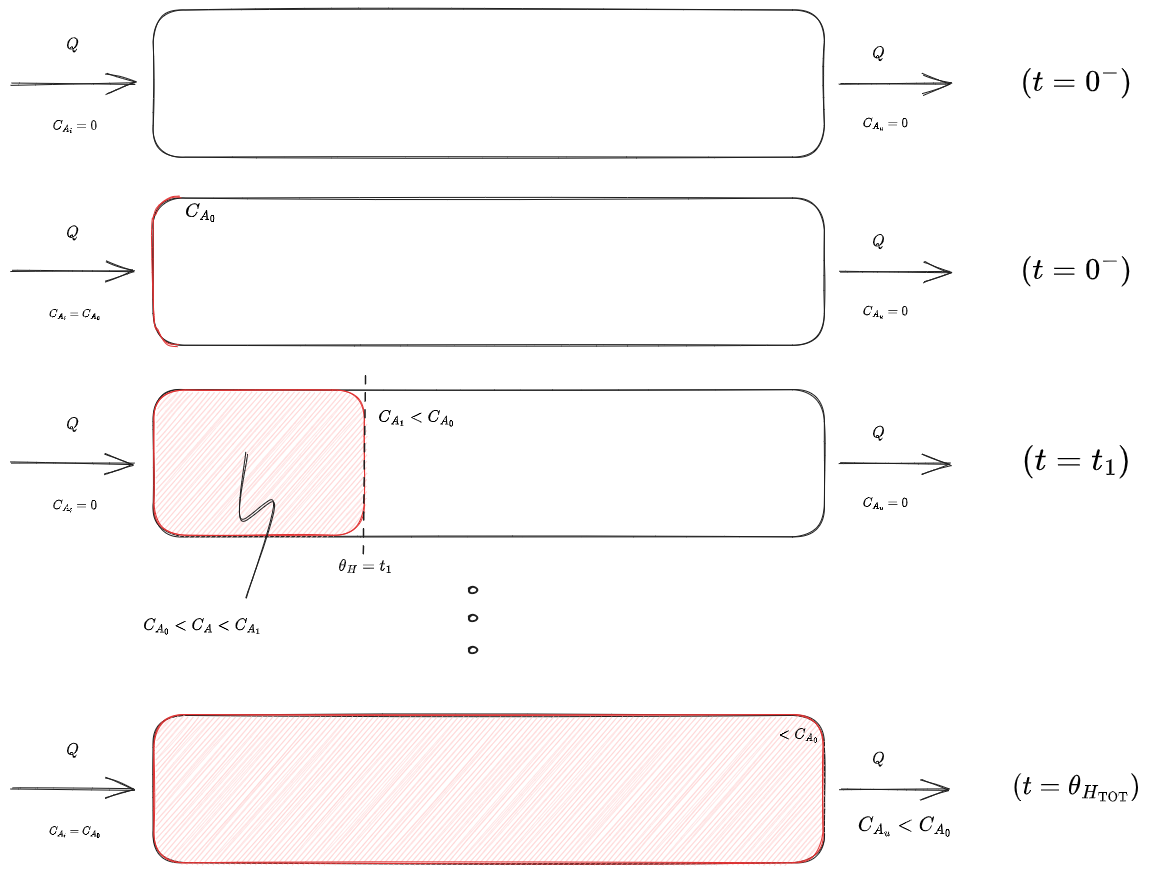
%%🖋 Edit in Excalidraw, and the dark exported image%%

Per ottenere gli andamenti delle concentrazioni risolviamo l'equazione:

\frac{d C_{A}}{d θ_{H}} = r_{A} = - k_{(0)} cond. stazionarie

integrando:

\int_{C_{A_{0}}}^{C_{A} (θ_{H})} d C_{A} = - k_{(0)} \int_{0}^{θ_{H}} d θ_{H}

che restituisce

cinetica di ordine 0 - pfr

$C_{A} (θ_{H}) = C_{A_{0}} - k_{(0)} θ_{H}$

Questa situazione porta ai seguenti diagrammi:

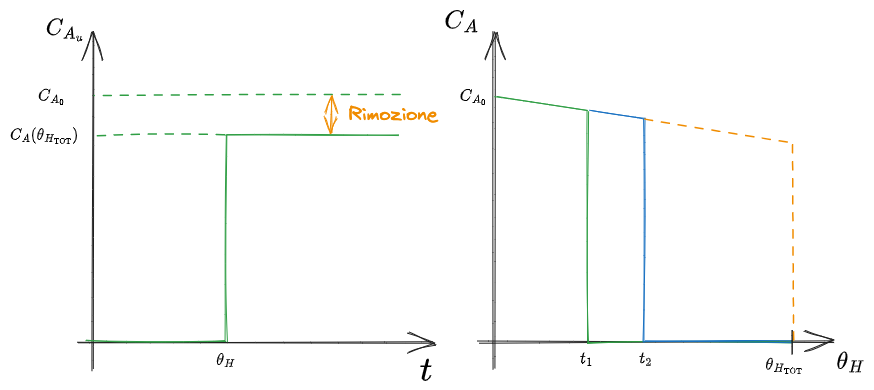
%%🖋 Edit in Excalidraw, and the dark exported image%%

3 - Cinetica di ordine 1 - Gradino - PFR

cinetica di ordine 1 - gradino - pfr

$C_{A} (θ_{H}) = C_{A_{0}} e^{- k_{(1)} θ_{H}}$

4 - Cinetica di ordine 2 - Gradino - PFR

cinetica di ordine 2 - gradino - pfr

$C_{A} (θ_{H}) = \frac{C_{A_{0}}}{1 + C_{A_{0}} k_{(2)} θ_{H}}$

5 - Cinetica di saturazione - Gradino - PFR

cinetica di saturazione - gradino - pfr

$K_{A} \ln \frac{C_{A}}{C_{A_{0}}} + C_{A} = C_{A_{0}} - k_{s} θ_{H}$

Segnale a impulso - PFR

Diversamente per quanto accade per il CFSTR, la risposta a un [[#Segnale a impulso]] per un [[#Reattore PFR]] è molto semplice. Non è altro, infatti, che lo stesso segnale traslato nel tempo.

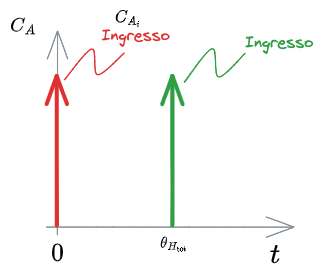
%%🖋 Edit in Excalidraw, and the dark exported image%%

Funzione di distribuzione - PFR

Si analizza di seguito il caso della [[#Funzione di distribuzione dei tempi di residenza]] di un [[#Reattore PFR]]. In questo caso è molto semplice in quanto il [[#Segnale a impulso - PFR]] non fa altro che traslare la risposta. Anche la funzione di distribuzione rimane invariata e avrà l'aspetto di un impulso.
Infatti tutte le particelle nel PFR hanno [[#Tempo di residenza idraulica]] $θ_{H} = θ_{H}^{*}$ .

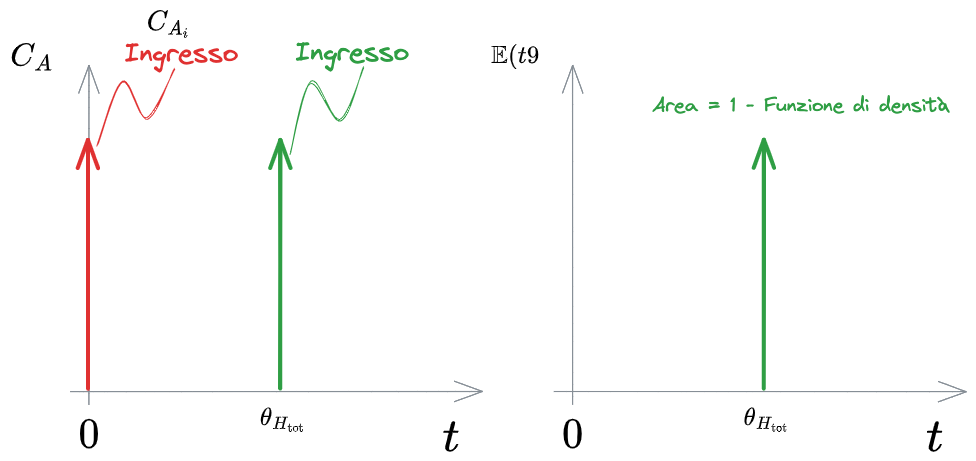
%%🖋 Edit in Excalidraw, and the dark exported image%%

Si noti che tutte le particelle di fluido di un [[#Reattore PFR]] hanno come [[#Tempo di residenza idraulica]] $θ_{H} = θ_{H_{T O T}}$ . Risulta pertanto migliore, chimicamente, del [[#Reattore CFSTR]].

Distribuzione dei tempi di residenza di un fluido all'interno di un reattore

[?] Rispiegare la distribuzione dei tempi di residenza.

!300	!300

Descrivere il funzionamento di un reattore in modo completo richiederebbe la conoscenza del campo di moto del fluido al suo interno. Questa può diventare un'operazione estremamente onerosa. Pertanto, si sceglie di studiare il comportamento dei reattori su scala globale.

Il grado di conversione ottenibile nel reattore, sarà dovuto al tempo che ogni particella ha a disposizione all'interno dello stesso, ossia, al [[#Tempo di residenza idraulica]].

Una descrizione globale del comportamento di un reattore a flusso arbitrario è pertanto ottenuta determinando, per ogni particella in ingresso, quale sarà il proprio tempo di residenza all'interno del reattore

Una descrizione di questo tipo è data attraverso la determinazione della cosiddetta [[#Funzione di distribuzione dei tempi di residenza]], $E (θ_{H})$ .

[[2023-10-17]]
[[Alessandra Polettini]]
![[Recording 20231017172134.webm]]
![[Recording 20231017183851.webm]]
%%

[[2023-10-19]]
[[Alessandra Polettini]]
![[Recording 20231019153134.webm]]
![[Recording 20231019164613.webm]]
%%

[[2023-10-20]]
[[Alessandra Polettini]]
![[Recording 20231020144223.webm]]
%%

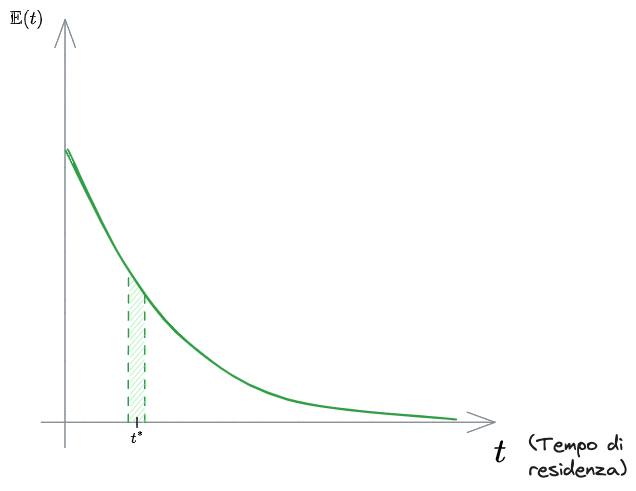
Funzione di distribuzione dei tempi di residenza

funzione di distribuzione dei tempi di residenza ($\mathbb{e}(\theta_{h})$)

La funzione di distribuzione dei tempi di residenza è una funzione che, per ogni [[#Tempo di residenza idraulica]] possibile, restituisce quale frazione di particdelle ha proprio quel tempo di residenza.

Nel grafico sottostante è raffigurato l'andamento di una generica $E (t)$ .

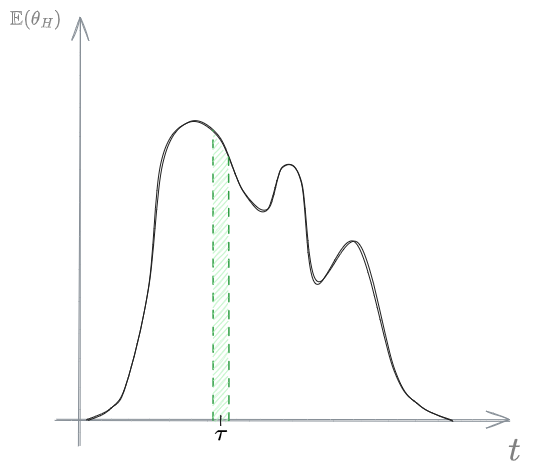
%%🖋 Edit in Excalidraw, and the dark exported image%%

La $E$ può essere vista come una densità di probabilità per cui, l'aureola infinitesima $E (τ) d t$ , centrata nell'istante $τ$ , rappresenta la probabilità che gli elementi di fluido abbiano un [[#Tempo di residenza idraulica]] compreso $[τ - \frac{d t}{2}, τ + \frac{d t}{2}]$ .

Detto ciò, si può dire che

\int_{0}^{τ} E (t) d t = [\begin{matrix} Frazione di particelle \\ con tempo di residenza < τ \end{matrix}]

La Funzione di distribuzione dei tempi di residenza, gode di tutte le proprietà di una densità di probabilità.

\int_{0}^{\infty} E (t) d t = 1

osservazione

Poiché la funzione $E (t)$ dipende dal comportamento idraulico del reattore, ovvero dal percorso seguito dai singoli elementi fluidi all'interno del reattore, essa non dipende in alcun modo dal tipo di segnale in applicato al reattore.

Il comportamento del reattore, d'altro canto, dipende sia dalla funzione $E$ , sia al tipo di segnale applicato.

[?] Perché la funzione di distribuzione non dipende dal tipo di segnale applicato al reattore?
- E(t) caratterizza il reattore dal punto di vista di quanto le particelle rimangono nel reattore. Non può dipendere dal segnale. Se a un certo istante inserisco tot particelle, se un reattore è di un certo tipo, le particelle si distribuiscono dal punto di vista del tempo di residenza in un certo modo.

Siamo ora interessati a trovare la funzione di ripartizione. In particolare vorremmo ricavarla in maniera sufficientemente semplice, una volta nota la risposta a un determinato segnale in ingresso.

Si segue l'[[#Analisi Stimolo-Risposta]]: si misura cioè la risposta di un reattore nel quale è iniettato un tracciante con una legge di variazione della concentrazione assegnata.

Siccome abbiamo detto che la $E (t)$ non dipende dal segnale in ingresso, per un generico reattore osserviamo cosa succede in risposta a un [[#Segnale a impulso]].

%%🖋 Edit in Excalidraw%%

L'aureola verde, $C_{A_{u}} (τ) d t$ , rappresenta la concentrazione in uscita dal reattore in funzione del tempo. Essa è inoltre proporzionale, a meno di una portata $Q$ , alla quantità di particelle uscenti dal reattore nell'intervallo $[τ - \frac{d t}{2}, τ + \frac{d t}{2}]$ .

Essendo il segnale in ingresso un segnale a impulso, tutte le particelle entrano nel reattore nello stesso istante $t = 0$ . Per questo motivo, le particelle che escono dal reattore al tempo $τ$ , sono quelle rimaste nel reattore proprio un tempo $τ$ , ovvero hanno avuto [[#Tempo di residenza idraulica]] $θ_{H} = τ$ . Quindi, l'aureola $C_{A_{u}} (τ) d t$ rappresenta la quantità di particelle il cui tempo di residenza è proprio $τ$ .

Se ora si immagina di tracciare l'andamento di $C_{u}$ adimensionalizzando con l'area complessiva della curva $C_{A} (t)$ , si ottiene una curva $C (t)$ la cui aureola in $τ$ rappresenta la porzione (frazione, percentuale) di particelle sul totale che hanno avuto tempo di residenza proprio $τ$ . Si tratta di fatto della [[#Funzione di distribuzione dei tempi di residenza]] $E (t)$ che stavamo cercando.

Detto ciò si può trovare l'espressione analitica della $E (t)$ per un [[#Reattore CFSTR]]:

Funzione di distribuzione - CFSTR

Si vuole cercare la [[#Funzione di distribuzione dei tempi di residenza]] per un [[#Reattore CFSTR]].

Per quanto detto in [[#Funzione di distribuzione dei tempi di residenza]], $E (t)$ può essere espressa come rapporto tra la quantità di particelle con tempo di residenza pari a $τ$ e la quantità totale di particelle (integrale sotto la curva $C_{u} (t)$ ):
$E (t) = \frac{Massa di tracciante che ha avuto θ_{H} \sim t^{*}}{\int_{0}^{\infty} C_{u} (t) d t}$
a meno delle portate $Q$ .

Nel caso di un [[#Segnale a impulso - CFSTR]] (ricordo di aver preso ad esempio il [[#Segnale a impulso]]), la risposta del reattore, $C_{u} (t)$ è
$C_{A_{u}} (t) = C_{A_{0}} e^{- \frac{t}{θ_{H}}}$
Integrando tra 0 e $\infty$ si ha:
$\int_{0}^{\infty} C_{u} (t) d t = \int_{0}^{\infty} C_{A_{0}} e^{- \frac{t}{θ_{H}}} d t = C_{A_{0}} θ_{H}$
La [[#Funzione di distribuzione dei tempi di residenza]] nel caso di un [[#Reattore CFSTR]] è quindi:
$E (t) = \frac{C_{A_{0}} e^{- \frac{t}{θ_{H}}}}{C_{A_{0}} θ_{H}} = \frac{e^{- \frac{t}{θ_{H}}}}{θ_{H}}$

[?] Perché la funzione di distribuzione è moltiplicata per $d θ_{H}$ ? Se è il rapporto tra la massa di tracciante con tempo di residenza paro a $t^{*}$ e la massa totale in ingresso, perché la moltiplico per un tempo?

Possiamo scrivere, ricordando quanto detto sulla funzione di distribuzione.
$E (θ_{H}^{*}) d θ_{H} = \frac{Massa di tracciante che ha avuto θ_{H} \sim t^{*}}{M_{A_{0}}}$

[?] Perché la funzione di distribuzione è moltiplicata per $d θ_{H}$ ? Se è il rapporto tra la massa di tracciante con tempo di residenza paro a $t^{*}$ e la massa totale in ingresso, perché la moltiplico per un tempo?

che può essere riscritta (ricordando come esprimere la massa da [[#Segnale a impulso - CFSTR]] - si tenga a mente che la [[#Funzione di distribuzione dei tempi di residenza]] non dipende dal segnale in ingresso). $M_{A_{0}}$ è calcolata come massa totale uscente dal reattore.
$E (θ_{H}^{*}) d θ_{H} = \frac{C_{A_{u}} (t^{*}) d t}{\int_{0}^{\infty} C_{A_{u}} (t) d t}$
Sostituendo a $C_{A_{u}}$ l'espressione
$C_{A_{u}} (t) = C_{A_{0}} e^{- \frac{t}{θ_{H}}}$
ottengo
$E (t^{*}) d t = \frac{C_{A_{u}} (t^{*}) d t}{\int_{0}^{\infty} C_{A_{u}} (t) d t} = \frac{C_{A_{0}} e^{- \frac{t^{*}}{θ_{H}}}}{C_{A_{0}} θ_{H}}$
che restituisce in definitiva
$E (t) = \frac{e^{- \frac{t}{d θ_{H}}}}{θ_{H}}$
che è l'andamento della funzione di distribuzione per un [[#Reattore CFSTR]].
%%

03. Reattori Ideali 2023-10-26 12.38.06.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

Essendo l'andamento un'esponenziale decrescente, notiamo che ci sarà sempre una certa frazione di particelle che non escono mai dal reattore.

Inoltre è evidente che ogni particella abbia un valore di $θ_{H}$ differente.
Calcoliamo ora il valor medio di $θ_{H}$ : ${\overset{―}{θ}}_{H}$
${\overset{―}{θ}}_{H} = \int_{0}^{\infty} t E (t) d t = \int_{0}^{\infty} \frac{t e^{- \frac{t}{θ_{H}}}}{θ_{H}} d t \overset{(\dots)}{=} θ_{H} = \frac{V}{Q}$

Si procede ora al calcolo per un [[#Reattore PFR]]:

Funzione di distribuzione - PFR

03. Reattori Ideali 2023-10-28 17.13.32.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

osservazione

La funzione $E (t)$ dipende soltanto dal comportamento idraulico del reattore e non dipende dal tipo di segnale applicato.
(questo vale in generale)

Integrale di convoluzione

Si immagini di inserire in un generico reattore una specie tracciante $A$ , con una assegnato segnale in ingresso $C_{A_{i}} (t)$ . A questo segnale il reattore risponderà con un certo andamento di concentrazione in uscita, $C_{A_{u}} (t)$ .

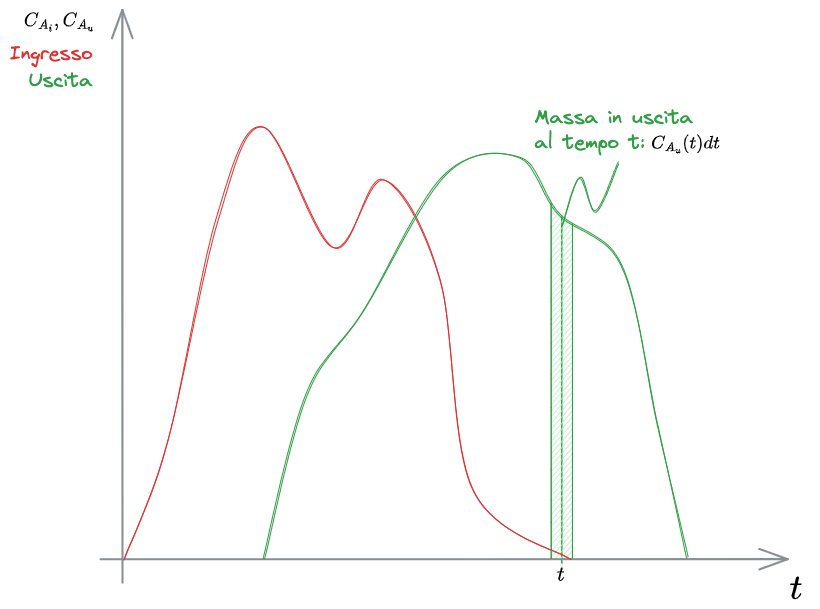
%%🖋 Edit in Excalidraw, and the dark exported image%%

Al generico istante $t$ , corrisponderà una certa quantità di particelle in uscita, $C_{A_{u}} (t) d t$ (a meno di una portata $Q$ ) - il rettangolo in verde.
Queste particelle, in generale, avranno ognuna tempi di residenza diversi.

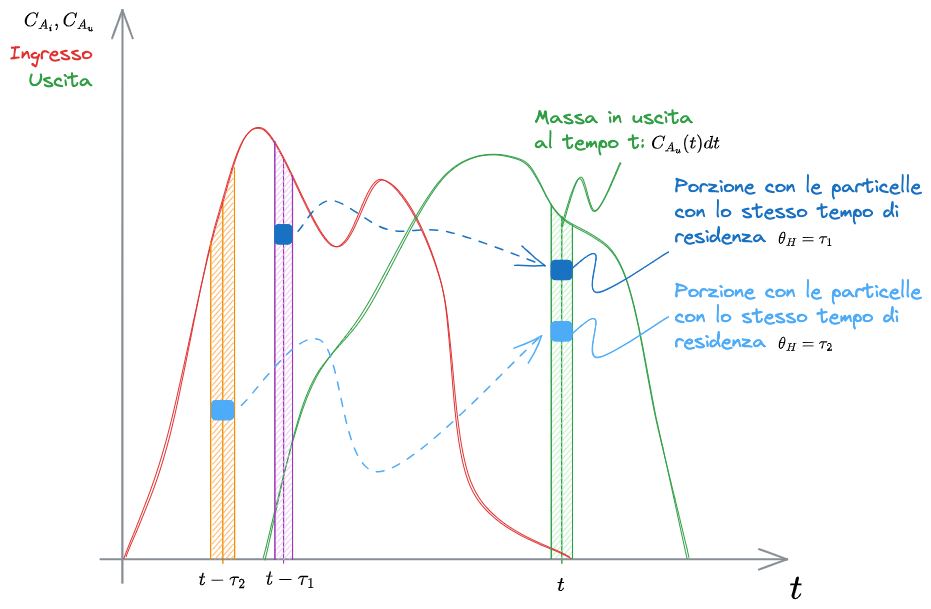
%%🖋 Edit in Excalidraw, and the dark exported image%%

Delle particelle in uscita nell'istante t, si considerino solo quelle che hanno avuto [[#Tempo di residenza idraulica]] pari a $τ_{1}$ (rettangolo blu).
Le stesse possono essere individuate sotto la curva $C_{A_{i}} (t)$ come porzione del rettangolo viola, all'istante $t - τ_{1}$ . La porzione del rettangolo vuota (delle particelle in ingresso a $t - τ_{1}$ ) con tempo di residenza pari a $τ_{1}$ è di nuovo identificata da un rettangolino blu.

Cosa del tutto analoga si può fare per la porzione delle particelle in uscita all'istante $t$ che abbiano avuto tempo di residenza pari a $τ_{2}$ . Queste saranno una qualche porzione (in blu) del rettangolo arancione, dove quest'ultimo individua tutte le particelle in ingresso al tempo $t - τ_{2}$ .

All'istante $t - τ_{1}$ , la frazione di particelle con tempo di residenza pari a $τ_{1}$ saranno, rispetto al totale delle entranti, individuate dalla [[#Funzione di distribuzione dei tempi di residenza]]. Ossia, la porzione di particelle che entra a $t - τ_{1}$ e che avrà tempo di residenza pari a $τ_{1}$ è $C_{A_{i}} (t - τ_{1}) E (τ_{j}) d τ$ .

Posso quindi pensare di esprimere la totalità delle particelle in uscita all'istante $t$ (l'area del rettangolo verde) come la somma delle varie porzioni (di tutti i $j$ -esimi rettangolini blu), ognuno dei quali sarà:

C_{A_{i}} (t - τ_{j}) E (τ_{j}) d τ

Posso quindi scrivere il triangolo verde ( $C_{A_{u}} (t) d t$ ) come:

C_{A_{u}} (t) d t = \sum_{j = 1}^{n} C_{A_{i}} (t - τ_{j}) E (τ_{j}) d τ

%%🖋 Edit in Excalidraw%%

che, al limite, si può scrivere come l'integrale:

C_{A_{u}} (t) = \int_{0}^{τ} C_{A_{i}} (t - τ) E (τ) d τ

conosciuto come l'[[#Integrale di convoluzione]].

integrale di convoluzione

L'integrale
$C_{A_{u}} (t) = \int_{0}^{τ} C_{A_{i}} (t - τ) E (τ) d τ$
è noto come integrale di convoluzione e permette, nota la segnale in ingresso a un reattore, di ricavare la risposta $C_{A_{u}} (t)$ del reattore stesso in funzione del tempo.

osservazione

Questo integrale vale nel caso della specie tracciante. In presenza di reazione, bisogna tenere conto anche della rimozione.

[[2023-10-24]]
[[Alessandra Polettini]]
![[Recording 20231024171107.webm]]
%%

Combinazioni di reattori

L'interesse primario nello studio dei [[#3. Reattori a Flusso Continuo Ideali]] è quello di poter in qualche modo descrivere i reattori reali, anche se diversi da un [[#Reattore CFSTR]] o [[#Reattore PFR]].
Per farlo si procede definendo alcune combinazioni di reattori.
Si possono avere

Reattori in Serie

Si immagini per il momento di guardare solo a [[#Reattore CFSTR]] in serie.

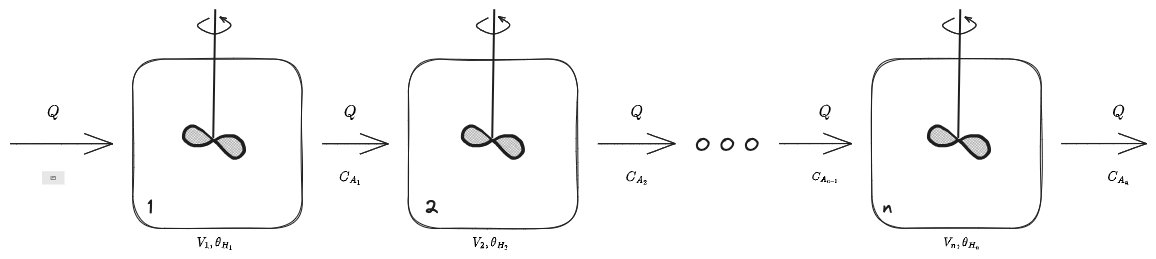
%%🖋 Edit in Excalidraw, and the dark exported image%%

Serie - Cinetica di ordine 0 - CFSTR

In uscita dal primo reattore si ha:

C_{A_{1}} = C_{A_{0}} - k_{(0)} θ_{H_{1}}

che sarà anche l'ingresso del secondo reattore. Quest'ultimo pertanto avrà in uscita:

C_{A_{2}} = C_{A_{1}} - k_{(0)} θ_{H_{2}} = C_{A_{0}} - k_{(0)} (θ_{H_{1}} + θ_{H_{2}})

Generalizzando per $n$ [[#Reattore CFSTR]] si ottiene in uscita:

C_{u} = C_{A_{0}} k_{(0)} \sum_{i = 1}^{n} θ_{H_{i}}

Si supponga ora di avere tutti tempi di residenza uguali:

θ_{H_{1}} = θ_{H_{2}} = \dots = θ_{H_{n}} \overset{△}{=} θ_{H}

si ottiene:

C_{A_{u}} = C_{A_{0}} - n k_{(0)} θ_{H}

da cui si ha:

θ_{H_{T O T}} = n θ_{H} = \frac{C_{A_{0}} - C_{A_{u}}}{k_{(0)}}

osservazione

Una serie di [[#Reattore CFSTR]] equivale a un unico reattore descritto da:
$C_{A_{u}} = C_{A_{0}} - θ_{H} k_{(0)}$
in cui
$θ_{H} = θ_{H_{T O T}}$

Serie - Cinetica di ordine 1 - CFSTR

La Concentrazione in uscita dai vari reattori dei [[#Reattori in Serie]] nel caso di [[#3 - Cinetica di ordine 1 - Gradino - CFSTR]] è data da

\begin{aligned} C_{A_{1}} & = \frac{C_{A_{0}}}{1 + k_{(1)} θ_{H_{1}}} \\ C_{A_{2}} & = \frac{C_{A_{1}}}{1 + k_{(1)} θ_{2}} = \frac{C_{A_{0}}}{(1 + k_{(1)} θ_{H_{1}}) (1 + k_{(1)} θ_{H_{2}})} \\ ⋮ \\ C_{A_{u}} & = \frac{C_{A_{0}}}{\prod_{i = 1}^{n} (1 + k_{(1)} θ_{H_{i}})} \end{aligned}

Si suppone, come nel caso di [[#Serie - Cinetica di ordine 0 - CFSTR]], di avere [[#Tempo di residenza idraulica]] tutti uguali. Allora

C_{A_{u}} = \frac{C_{A_{0}}}{(1 + k_{(1)} θ_{H})^{n}}

da cui si può ricavare

θ_{H} = [{(\frac{C_{A_{0}}}{C_{A_{u}}})}^{\frac{1}{n}} - 1] \frac{1}{k_{(1)}}

che fornisce un $θ_{H_{T O T}}$ di

θ_{H_{T O T}} = n θ_{H} = [{(\frac{C_{A_{0}}}{C_{A_{u}}})}^{\frac{1}{n}} - 1] \frac{n}{k_{(1)}}

La serie coincide con un unico reattore descritto da

C_{A_{u}} = \frac{C_{A_{0}}}{1 + k_{(1)} θ_{H}}

dove

θ_{H} = \frac{1}{k_{(1)}} (\frac{C_{A_{0}}}{C_{A_{u}}} - 1)

esempio

Supponiamo di avere una $C_{A_{u}} = 0.1 C_{A_{0}}$ e calcoliamo i [[#Tempo di residenza idraulica]] per vari numeri di reattori in serie:
$\begin{aligned} n = 1 & ⟹ θ_{H} = \frac{1}{k_{(1)}} (10 - 1) = \frac{9}{k_{(1)}} \\ n = 3 & ⟹ θ_{H} = \frac{3}{k_{(1)}} (10^{\frac{1}{3}} - 1) = \frac{3.46}{k_{(1)}} \\ n = 5 & ⟹ θ_{H} = \frac{5}{k_{(1)}} (10^{\frac{1}{5}} - 1) = \frac{2.92}{k_{(1)}} \end{aligned}$
Vediamo che $θ_{H}$ tende a diminuire all'aumentare di $n$ arrivando al limite ad essere uguale a 1. Questo comporta che all'aumentare dei reattori in serie, diminuisce il volume in gioco.

osservazione 1

Nei reattori PFR non c'è alcuna differenza tra un reattore unico e una serie di reattori.

osservazione 2

Una serie di $n$ [[#Reattore CFSTR]] con $n \to \infty$ fornisce un [[#Reattore PFR]].

03. Reattori Ideali 2023-10-31 13.08.20.excalidraw.png|03. Reattori Ideali 2023-10-31 13.08.20.excalidraw.png|450

[[2023-10-26]] - [[Alessandra Polettini]]
![[Recording 20231026153626.webm]]
![[Recording 20231026164627.webm]]
%%

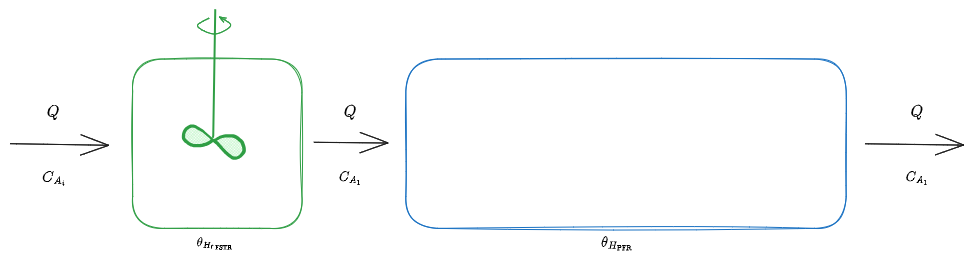
03. Reattori Ideali 2023-11-01 18.20.28.excalidraw.png
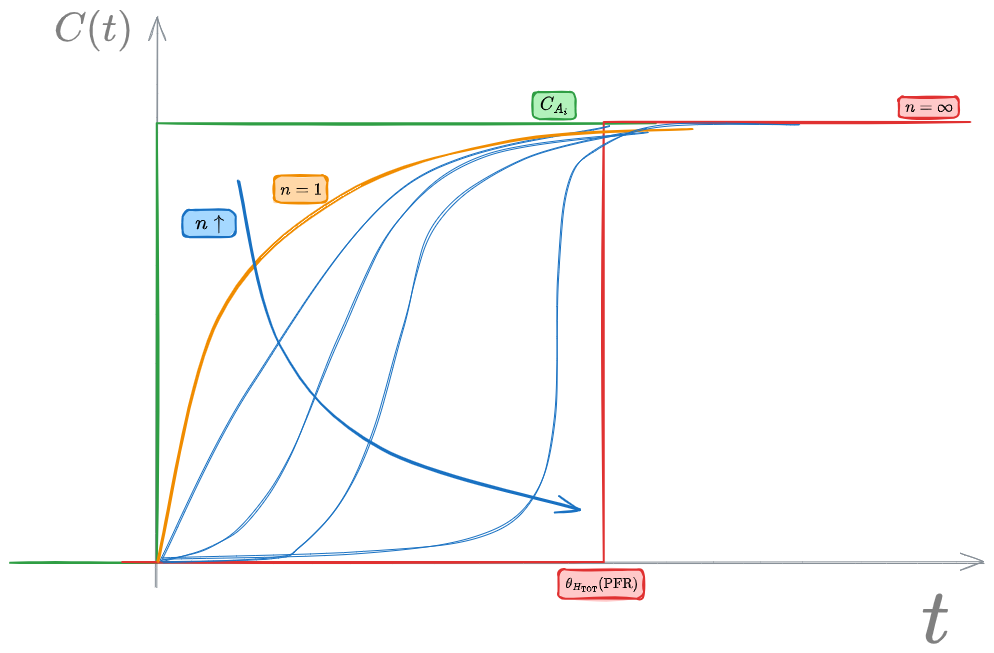
%%🖋 Edit in Excalidraw, and the dark exported image%%

Ai [[#Reattori in Serie]] mostrati in figura viene applicato un [[#Segnale a gradino]] in ingresso nel caso di specie tracciante ( $r_{A} = 0$ ).

Ricordando quanto detto in [[#1 - Specie tracciante - Gradino - CFSTR]] e [[#Segnale a gradino - PFR]] si può tracciare il seguente grafico:

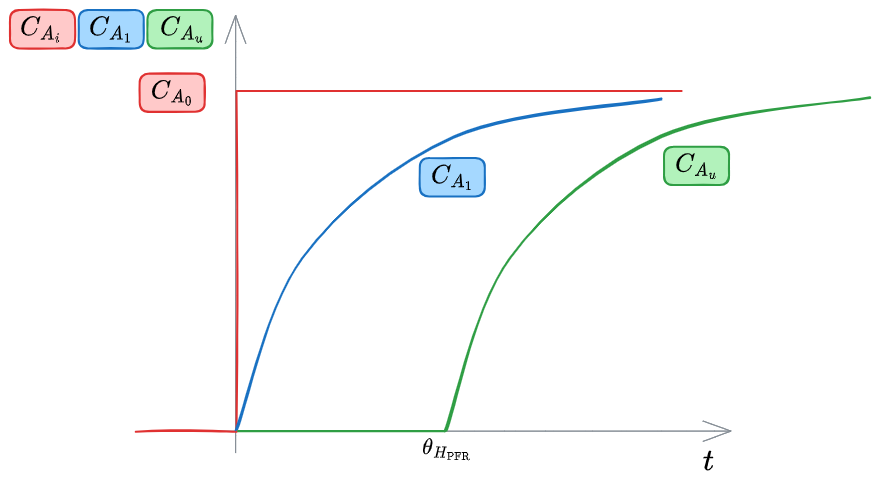
03. Reattori Ideali 2023-11-01 18.24.47.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

In questo caso $C_{A_{1}}$ diventa il segnale in ingresso del [[#Reattore PFR]] che non fa altro che produrre una traslazione di $θ_{H_{P F R}}$ della risposta.

Si ripete lo stesso ragionamento invertendo ora l'ordine dei due reattori:

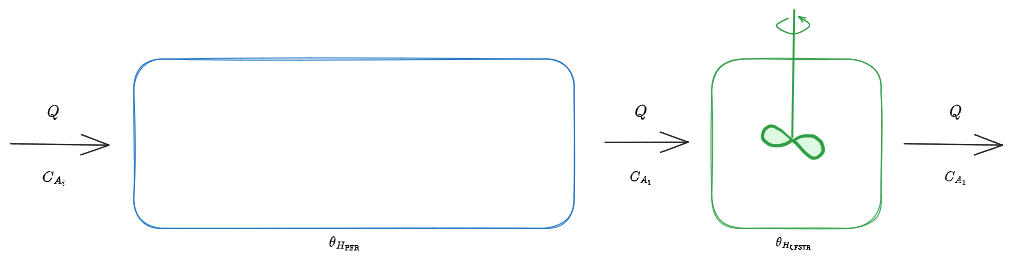
03. Reattori Ideali 2023-11-01 18.31.55.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

Il che porta ad una risposta che è mostrata nel grafico sottostante:

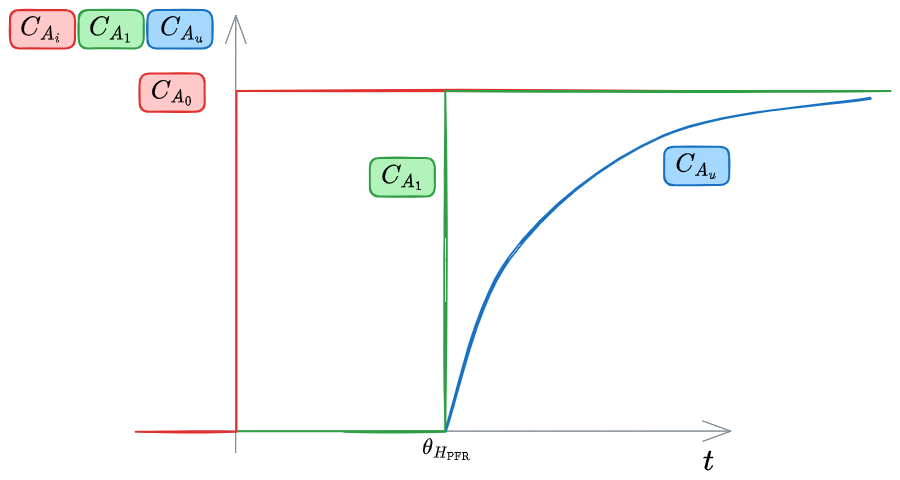
03. Reattori Ideali 2023-11-01 18.33.20.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image 🖋 Edit in Excalidraw, and the dark exported image%%

Reattori con ricircolo

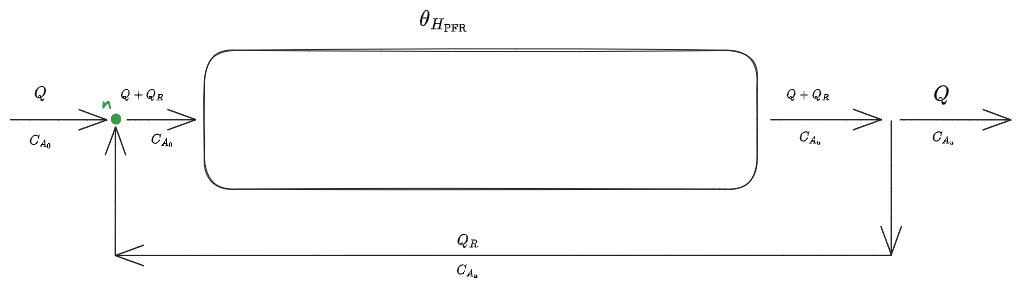
Reattori con ricircolo - Diagramma - 03. Reattori Ideali 2023-11-01 18.54.23.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image 🖋 Edit in Excalidraw, and the dark exported image 🖋 Edit in Excalidraw, and the dark exported image%%

Fluido si muove con velocità diverse lungo la stessa sezione.

Confronto efficienza tra CFSTR e PFR

Per confrontare il [[#Reattore CFSTR]] con [[#Reattore PFR]] si può procedere in due modi:

A parità di $C_{A_{0}}$ e $C_{A_{u}}$ confrontare i [[#Tempo di residenza idraulica]] $θ_{H}$
A parità di $C_{A_{0}}$ e $θ_{H}$ confrontare le concentrazioni in uscita $C_{A_{u}}$
Per la natura delle equazioni di [[#Bilancio di materia]], conviene il metodo 1.

Si ricorda da [[#Bilancio di materia - CFSTR]] e [[#Bilancio di materia - PFR]]:

\begin{matrix} CFSTR & PFR \\ Q C_{A_{0}} - Q C_{A_{u}} + r_{A} V = 0 & \frac{d C_{A}}{d θ_{H}} \\ - r_{A} = \frac{C_{a_{0}} - C_{A_{u}}}{θ_{H}} & \int_{C_{A_{0}}}^{C_{A_{u}}} \frac{1}{r_{A}} d C_{A} = \int_{0}^{θ_{H}} d θ_{H} \\ θ_{H} = - \frac{1}{r_{A}} (C_{A_{0}} - C_{A_{u}}) & \int_{C_{A_{u}}}^{C_{A_{0}}} - \frac{1}{r_{A}} d C_{A} = \int_{0}^{θ_{H}} d θ_{H} \end{matrix}

Quindi per il CFSTR, $θ_{H}$ è l'area del rettangolo blu, mentre per il PFR è l'area sottesa dalla curva, evidenziata in rosso

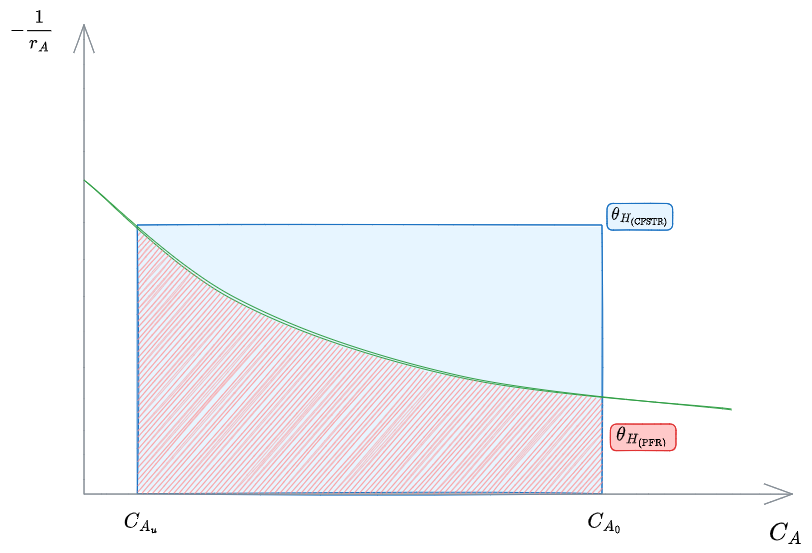
03. Reattori Ideali 2023-11-06 13.11.06.excalidraw.png|500
%%🖋 Edit in Excalidraw, and the dark exported image%%

Quindi, nel caso ci sia una relazione monotona tra $r_{A}$ e $C_{A}$ nei due reattori, il [[#Reattore PFR]] risulta essere più efficiente - ha [[#Tempo di residenza idraulica]] minore.

In caso di relazione generica non possiamo dire nulla a priori e tocca analizzare caso per caso.

Bacini di equalizzazione

Raramente i flussi $Q$ con cui si lavora sono flussi costanti nel tempo. Più frequente è avere flussi molto irregolari. Per lavorare al meglio però occorre avere a disposizione dei flussi costanti. Si può pertanto realizzare un bacino di equalizzazione, capace appunto di assolvere a questo compito.
I bacini di equalizzazione possono essere di due tipi:

Bacini di equalizzazione In Linea

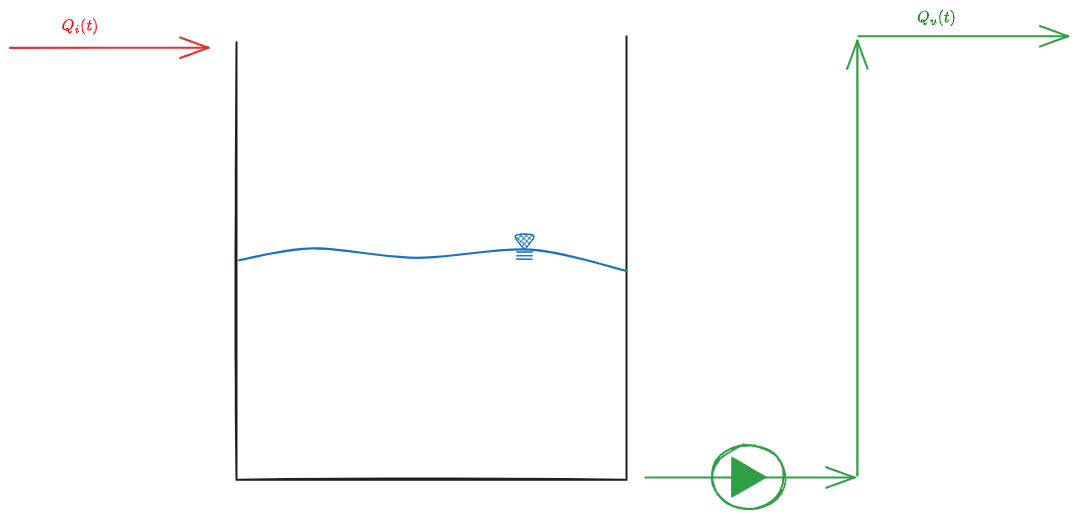
Bacini di equalizzazione in linea - diagramma - 03. Reattori Ideali 2023-11-09 12.02.10.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

Questo reattore vede entrare un certo carico idraulico. Il carico viene completamente perso quando il liquido passa dal bacino ma deve essere recuperato in toto alla fine.

Studiamo il funzionamento di questo equalizzatore come caso tipo. Ciò che viene detto è in realtà valido anche per i [[#Bacini di equalizzazione Fuori Linea]].

Condizione da rispettare assolutamente nella progettazione di un [[#Bacini di equalizzazione]] è che tutto il volume che ho in entrata lo devo prima o poi restituire in uscita.
Per semplicità inizialmente verrà considerato un intervallo temporale di $24 h$ .

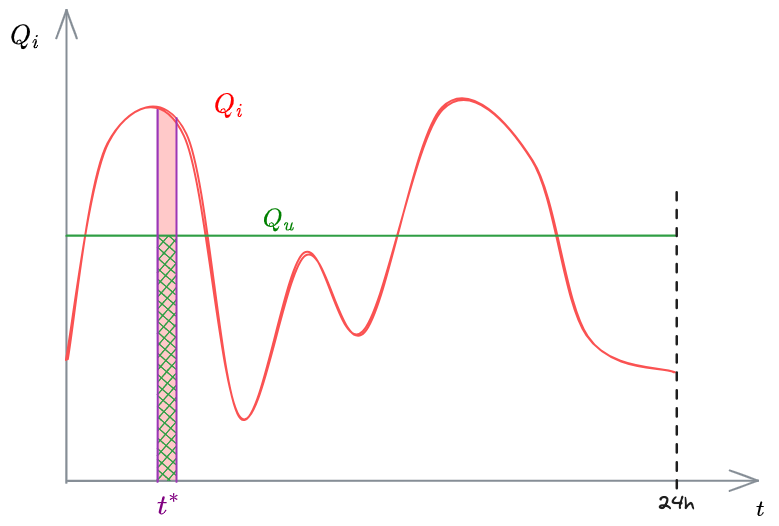
03. Reattori Ideali 2023-11-09 12.24.05.excalidraw.png|500
%%🖋 Edit in Excalidraw, and the dark exported image%%

Si lavora sui volumi.
Istantaneamente, in un istante $t^{*}$ , il volume in ingresso e in uscita è dato dai seguenti integrali.

{\begin{cases} V_{i, i s t} & = \int_{t^{*} - \frac{d t}{2}}^{t^{*} + \frac{d t}{2}} Q_{i} (t) d t \\ V_{u, i s t} & = \int_{t^{*} - \frac{d t}{2}}^{t^{*} + \frac{d t}{2}} Q_{u} (t) d t \end{cases}

Passando ai volumi comulati dall'istante 0 all'istante $t^{*}$ :

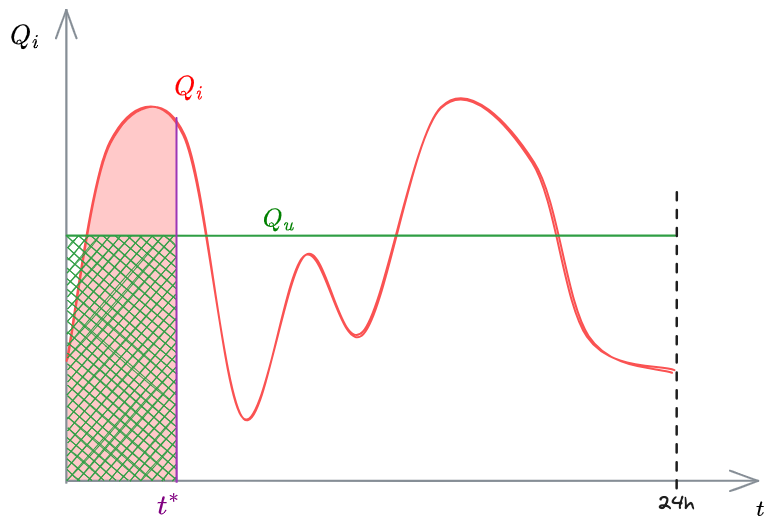
03. Reattori Ideali 2023-11-09 12.31.59.excalidraw.png|500
%%🖋 Edit in Excalidraw, and the dark exported image%%

Otteniamo i seguenti integrali:

{\begin{cases} V_{i, c u m} & = \int_{0}^{t^{*}} Q_{i} (t) d t \\ V_{u, c u m} & = \int_{0}^{t^{*}} Q_{u} (t) d t \end{cases}

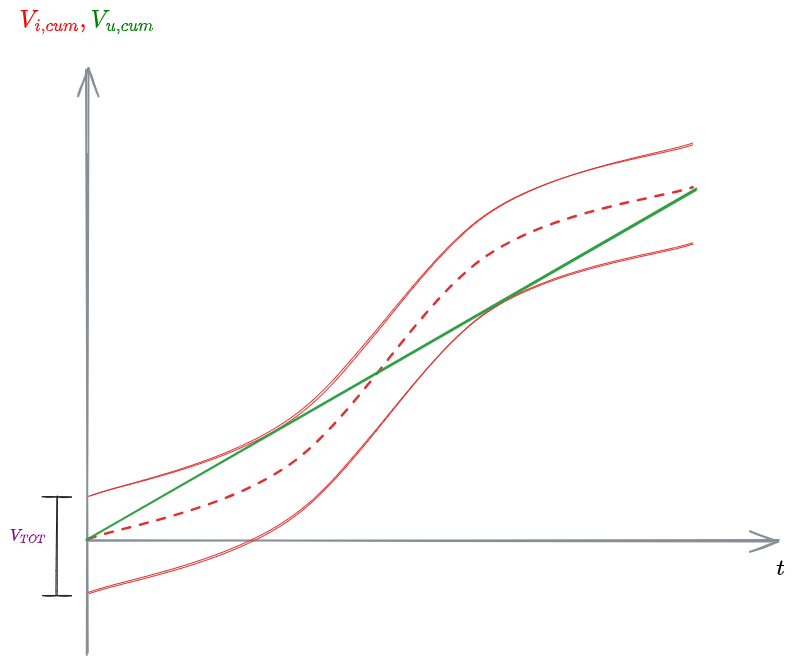
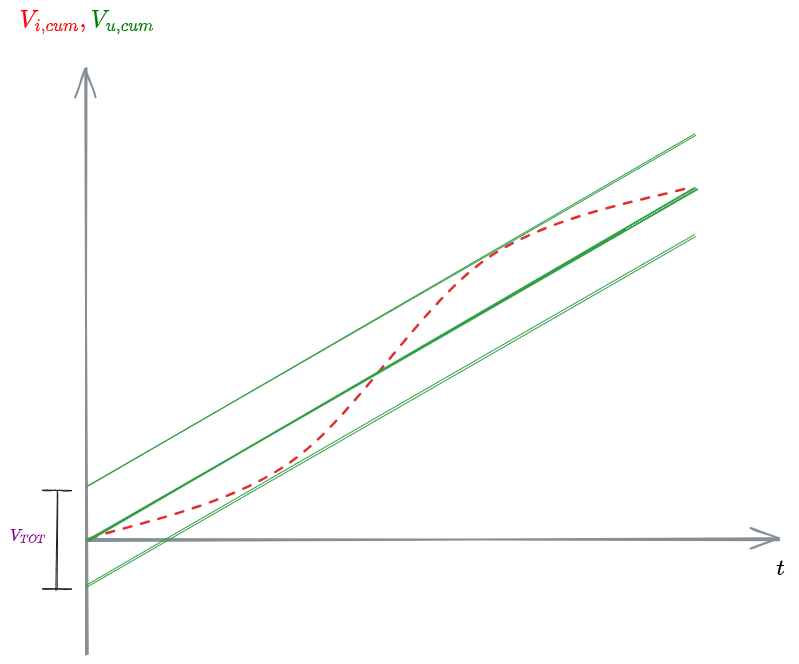
Quest'ultime, volendole graficare, saranno sicuramente curve crescenti, in quanto il volume totale che passa dall'equalizzatore non può che aumentare.

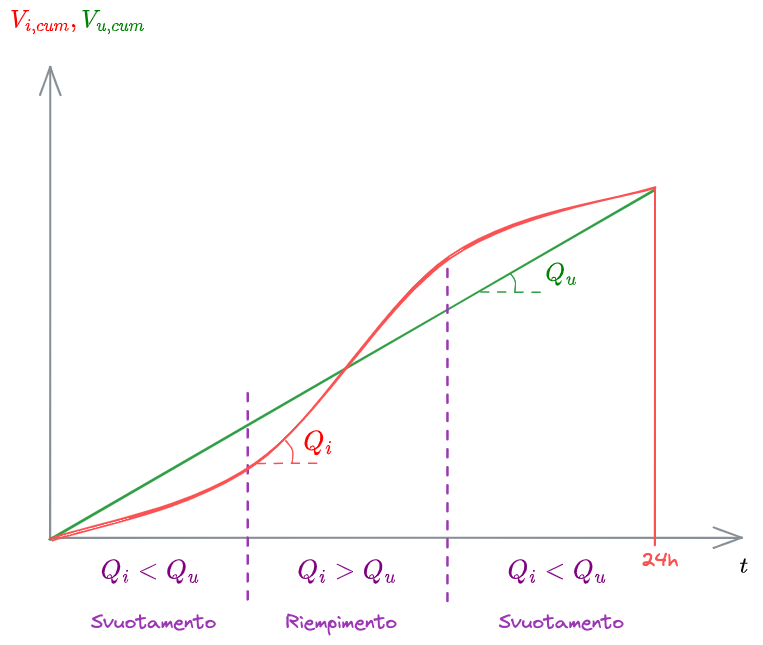
03. Reattori Ideali 2023-11-09 12.36.27.excalidraw.png|500
%%🖋 Edit in Excalidraw, and the dark exported image 🖋 Edit in Excalidraw, and the dark exported image 🖋 Edit in Excalidraw, and the dark exported image%%

Conoscendo l'andamento del volume in ingresso e del volume in uscita, come facciamo a capire quale sia il volume totale richiesto al bacino per funzionare correttamente?

Sapendo che il volume in uscita deve avere un andamento lineare, posso traslare la curva di volume in ingresso in modo da costruire una fascia tale che la curva di ingresso sia completamente contenuta in questa fascia. Sulle ordinate si legge così il volume tot necessario.

03. Reattori Ideali 2023-11-14 13.07.29.excalidraw.png|500
%%🖋 Edit in Excalidraw%%

Un modo più semplice di ricavare il $V_{T O T}$ è la [[#Regola del filo teso]]

Da questo grafico si possono ricavare i volumi entrati e usciti fino al tempo $t$ secondo gli integrali:

\begin{array}{r} V_{i, c u m} = \int_{0}^{t} Q_{i} (t) d t \\ V_{u, c u m} = \int_{0}^{t} Q_{u} (t) d t \end{array}

Regola del filo teso

La regola del filo teso è un metodo per ricavare il volume necessario a un [[#Bacini di equalizzazione]].
Consiste nel traslare la curva che descrive il volume in uscita desiderato:

03. Reattori Ideali 2023-11-14 13.11.20.excalidraw.png|500
%%🖋 Edit in Excalidraw%%

%%
[[2023-10-31]] - [[Alessandra Polettini]]
![[Recording 20231031171305.webm]]
%%

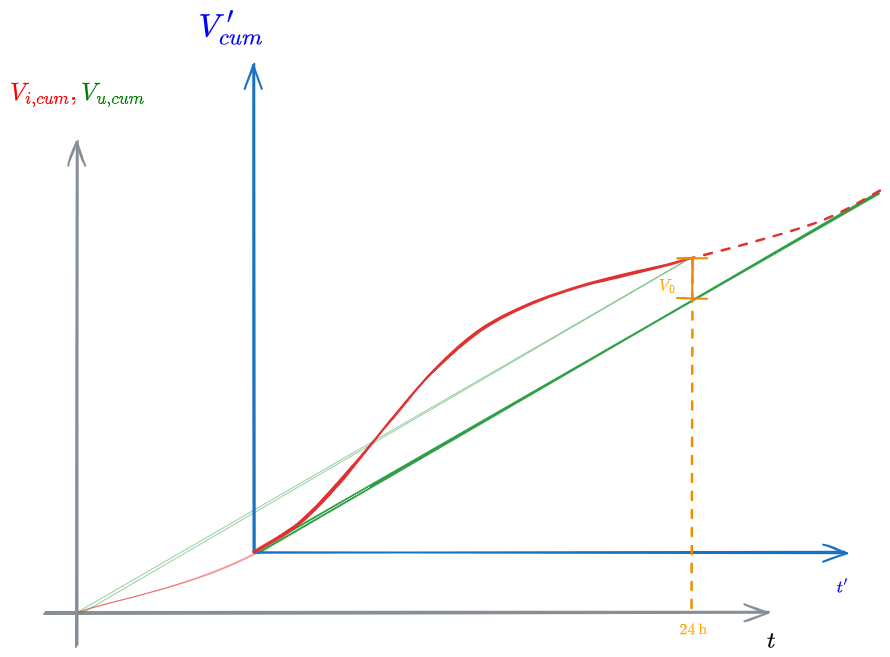
Misurazione dei tempi

È ragionevole pensare di porre l'origine del tempo nella condizione di bacino vuoto, aggiungendo dei nuovi assi $t^{'}, V_{c u m}^{'}$ .

Si può quindi notare che la curva di uscita non risulta mai maggiore di quella di ingresso.
La differenza

V_{i, c u m} - V_{u, c u m} > 0

In questo modo la differenza appena scritta rappresenta di volta in volta il volume residuo.

V_{R} (t^{'}) = V_{i, c u m} (t^{'}) - V_{u, c u m} (t^{'})

03. Reattori Ideali 2023-11-15 16.43.23.excalidraw.png|500
%%🖋 Edit in Excalidraw%%

\begin{array}{r} V_{i, c u m}^{'} = \int_{0}^{t^{'}} Q_{i} (t^{'}) d t \\ V_{u, c u m}^{'} = \int_{0}^{t^{'}} Q_{u} (t^{'}) d t \end{array}

In questo modo, posso sapere, alla fine delle 24h (contate sull'asse t) quale sia il volume residuo nel bacino. Questo sarà infatti dato dalla differenza

V_{0} = V_{i, c u m}^{'} (t = 24 h) - V_{u, c u m}^{'} (t = 24 h)

e quindi $V_{0}$ rappresenta il volume residuo nel bacino al giorno dopo.

Bacini di equalizzazione Fuori Linea

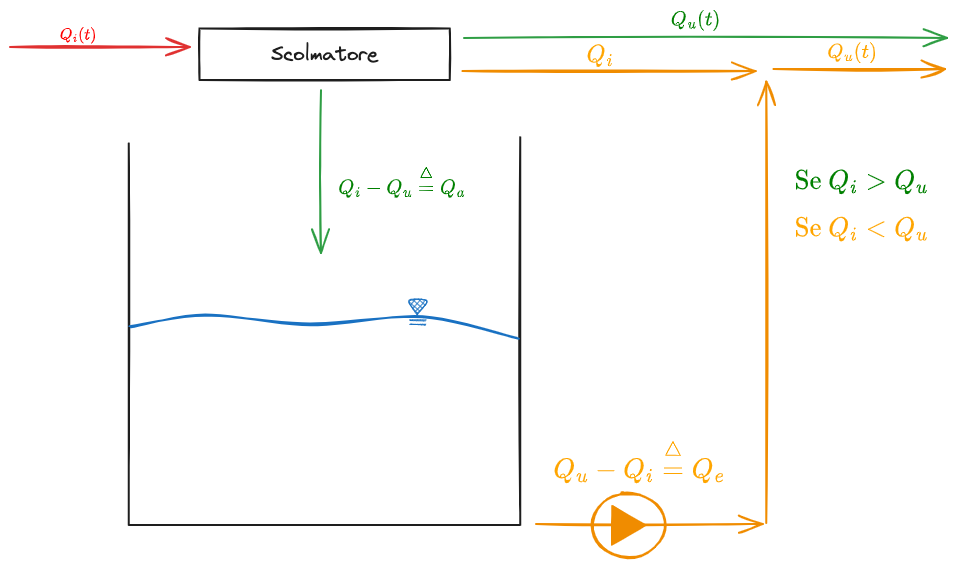
Bacino di equalizzazione fuori linea - Diagramma - 03. Reattori Ideali 2023-11-09 12.08.58.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

Voglio una certa $Q_{u}$ fissata. Posso avere 3 casi:

$Q_{i} = Q_{u}$ : tutto quello che entra, esce dallo scolmatore
$Q_{i} > Q_{u}$ : Ho fluido in eccesso, che viene scolmato nel bacino
$Q_{i} < Q_{u}$ : Mi manca del fluido per raggiungere $Q_{u}$ , quindi lo prelevo dal bacino

%%
[[2023-10-27]] - [[Alessandra Polettini]]
🎤 [[Recording 20231027144002.webm]]
%%

Effetto dell'equalizzazione delle portate sull'andamento della concentrazione

Schematizziamo il bacino come un [[#Reattore CFSTR]]:

$r_{A} = 0$
[[#Reattore CFSTR]]
Il volume è variabile

03. Reattori Ideali 2023-11-15 16.56.15.excalidraw.png|400
%%🖋 Edit in Excalidraw%%

Sotto queste ipotesi si prova a risolvere l'equazione di [[#Bilancio di materia - CFSTR]]:

\begin{array}{r} \frac{d V_{R} C_{A_{u}}}{d t} = Q_{i} C_{A_{i}} - Q_{u} C_{A_{u}} \\ V_{R} \frac{d C_{A_{u}}}{d t} + C_{A_{u}} \frac{d V_{R}}{d t} = Q_{i} C_{A_{i}} - Q_{u} C_{A_{u}} \end{array}

Si considera vuoto il bacino all'istante $t = 0$ .
Si ha:

\frac{d V_{R}}{d t} = {\begin{cases} > 0 ⟹ R i e m p i p e n t o \\ < 0 ⟹ S v u o t a m e n t o \end{cases}

$V_{R}$ è il volume residuo. Ricordando che:

\begin{array}{r} V_{i, c u m} = \int_{0}^{t} Q_{i} (t) d t \\ V_{u, c u m} = \int_{0}^{t} Q_{u} (t) d t \end{array}

e che

V_{R} = V_{i, c u m} - V_{u, c u m}

possiamo dire che

\frac{d V_{R}}{d t} = Q_{i} - Q_{u}

Quindi il bilancio scritto sopra diventa:

\begin{aligned} V_{R} \frac{d C_{A_{u}}}{d t} + C_{A_{u}} (Q_{i} - Q_{u}) & = Q_{i} C_{A_{i}} - Q_{u} C_{A_{u}} \\ \frac{d C_{A_{u}}}{d t} & = \frac{Q_{i}}{V_{R}} (C_{A_{i}} - C_{A_{u}}) \end{aligned}

Si ha quindi che:

\frac{d C_{A_{u}}}{d t} = \frac{Q_{i}}{V_{R}} (C_{A_{i}} - C_{A_{u}}) = {\begin{cases} > 0 & (C_{A_{u}} crescente) & per C_{A_{i}} > C_{A_{u}} \\ = 0 & (C_{A_{u}} \max / \min) & per C_{A_{i}} = C_{A_{u}} \\ < 0 & (C_{A_{u}} decrescente) & per C_{A_{i}} < C_{A_{u}} \end{cases}

Immaginiamo ora di avere

\frac{d C_{A}}{d t} = 0

Vogliamo capire se siamo nella condizione di minimo o massimo della concentrazione; uso la derivata seconda.
(...)

\frac{d^{2} C_{A_{u}}}{d t^{2}} = \frac{Q_{i}}{V_{R}} \frac{d C_{A_{i}}}{d t} \overset{?}{⋚} 0

Se maggiore di zero si ha concentrazione in uscita minima e quindi concentrazione in ingresso crescente, altrimenti massima in uscita e decrescente in ingresso.

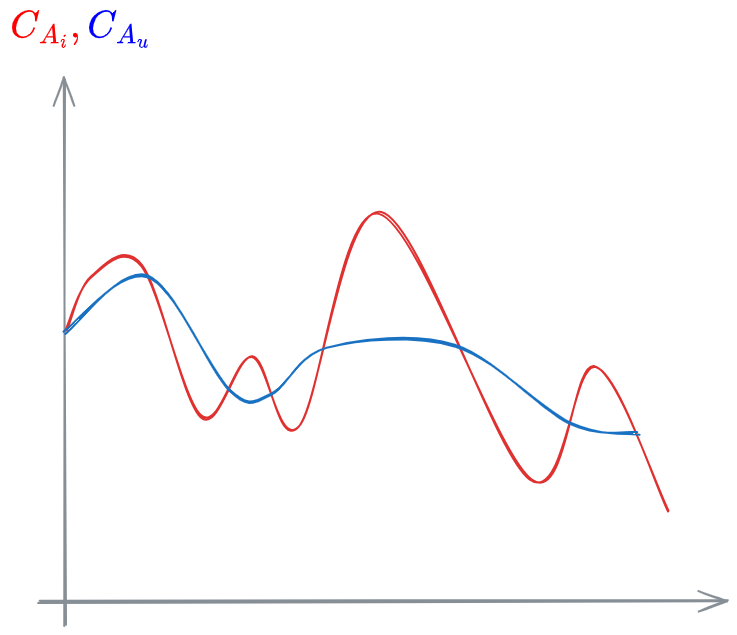
03. Reattori Ideali 2023-11-15 17.30.44.excalidraw.png|500
%%🖋 Edit in Excalidraw%%

Si noti che i massimi e i minimi delle concentrazioni in uscita sono sempre smorzati rispetto a quelli in ingresso. L'ampiezza delle oscillazioni è minore. E le oscillazioni sono più dilatate nel tempo (i picchi sono più lontani).

Ci piace lavorare in condizioni stazionarie. Questo smorzamento ci avvicina a queste condizioni

Il bacino di equalizzazione, oltre a equalizzare le portate, produce l'effetto di smorzare le oscillazioni della concentrazione.