02. Cinetica delle reazioni chimiche

2. Cinetica delle reazioni chimiche

\underset{r e a g e n t e}{A} ⟺ \underset{p r o d o t t o}{P}

Ci occupiamo dello studio delle reazioni chimiche.
In particolare nell'Ingegneria sanitaria ambientale vogliamo studiare le reazioni chimiche per trasformare gli inquinanti.

reattore

Potremmo definire un reattore come un sistema di reazioni.

Guarderemo due aspetti:

Termodinamico: Equilibrio termodinamico
Cinetico: Per noi è importante sapere in quanto tempo si completa una reazione

Classificazione delle reazioni chimiche

Posso seguire diversi approcci per classificare le reazioni chimiche:

#Classificazione per Natura dei componenti
#Classificazione per Verso della reazione
#Classificazione per Numero di stadi
#Classificazione per Sequenza degli stadi

Classificazione per Natura dei componenti

In termini di natura dei componenti una reazione può essere classificata in:

#Reazione omogenea
#Reazione Eterogenea

Reazione omogenea

reazione omogena

Una reazione si dice omogenea se tutte le specie si trovano nella stessa fase.

Reazione eterogenea

reazione eterogenea

Una reazione si dice eterogenea se sono presenti specie in fasi diverse.

Interfaccia

interfaccia

Nel caso in cui si abbia una [[#Reazione eterogenea]], l'area di contatto tra le diverse fasi è detta interfaccia.

Classificazione per Verso della reazione

In termini di verso di reazione, si può avere:

#Reazione Reversibile
#Reazione Irreversibile

Reazione Reversibile

Reazione Irreversibile

Nonostante la maggior parte delle reazioni nel nostro campo risulti reversibile, se ci si trova sufficientemente lontani dalle condizioni di equilibrio, e quindi la concentrazione dei prodotti risulta piccola, la #Velocità di reazione inversa sarà molto piccola rispetto a quella della reazione diretta. In questo caso parleremo di reazioni irreversibili

Classificazione per Numero di stadi

Stadio singolo

R ⟶ P

Stadi multipli

R ⟶ \dots ⟶ P

Classificazione per Sequenza degli stadi

Reazione con stadi in serie

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

Il passaggio da Reagenti a Prodotti avviene passando per fasi intermedie:

R ⟶ \dots ⟶ P

Reazione con stadi in parallelo

Si parla di reazioni con stadi in parallelo quando lo stesso reagente +è coinvolto in più di una reazione.

R \begin{matrix} ↗ P_{1} \\ ↘ P_{2} \end{matrix}

Velocità di reazione

Uno degli indicatori principali per descrivere una reazione è la velocità di reazione. Questa può essere vista come la massa (o il numero di moli) di reagente che scompare o del prodotto che appare, nell'unità di tempo.

velocità di reazione

$r_{A} = {\begin{cases} \frac{d N_{A}}{d t} \cdot \frac{1}{V} [\frac{m o l}{l \cdot s}] (o m o g e n e a) \\ \frac{d N_{A}}{d t} \cdot \frac{1}{S} (e t e r o g e n e a) \end{cases}$

Definisco la #Concentrazione Molare

Concentrazione Molare

concentrazione molare

$C_{A} = \frac{N_{A}}{V}$

Velocità di reazioni in reazioni omogenee

r_{A} = \frac{1}{V} \cdot \frac{d N_{A}}{d t}

Posso pensare di usare la concentrazione al posto della massa:

Per cui si ha che:

N_{A} = C_{A} V

\begin{aligned} r_{A} & = \frac{1}{V} \frac{d (C_{A} V)}{d t} = \\ = \frac{1}{V} (V \frac{d C_{A}}{d t} + C_{A} \frac{d V}{d t}) \overset{V = c o s t .}{=} \frac{d C_{A}}{d t} \end{aligned}

e quindi:

$r_{A} = \frac{d C_{A}}{d t}$

La #Velocità di reazione sarà pertanto negativa in quanto il reagente si consuma e quindi la sua concentrazione diminuisce.

r_{A} = \frac{d C_{A}}{d t} < 0

La velocità di reazione è alterata da:

Concentrazione
Condizioni termodinamiche (pressione, temperatura...)
Presenza di catalizzatori o inibitori

Considerando un sistema ideale senza catalizzatori o inibitori, e a pressione atmosferica e temp cost.

Vediamo la formulazione analitica della relazione tra #Velocità di reazione e concentrazione
Si hanno 2 casi:

#Cinetiche di ordine alpha
#Cinetiche di saturazione

r_{A} = {\begin{cases} - k_{(α)} C_{A}^{α} & Cinetiche di ordine α \\ - \frac{k_{s} C_{A}}{K_{A} + C_{A}} & Cinetiche di saturazione \end{cases}

Cinetiche di ordine alpha

cinetiche di ordine alpha

$r_{A} = - k_{(α)} C_{A}^{α}$
Dove:

$α =$ #Ordine di reazione
$k_{(α)} =$ [[#Costante di velocità]]

Con $0 < α < 3$ . Non si ha evidenza sperimentale di $α > 3$ .
Nei casi comuni: $0 < α < 2$ .

Noi faremo riferimento a valori di $α \in {0, 1, 2}$

\begin{aligned} α & = 0 & r_{A} & = - k_{(0)} C_{A}^{0} = - k_{(0)} & k_{(0)} & = [\begin{array}{c} \frac{m o l}{l \cdot s} \end{array}] \\ α & = 1 & r_{A} & = - k_{(1)} C_{A} & k_{(1)} & = [\begin{array}{c} \frac{1}{s} \end{array}] \\ α & = 2 & r_{A} & = - k_{(2)} C_{A}^{2} & k_{(2)} & = [\begin{array}{c} \frac{l}{m o l \cdot s} \end{array}] \end{aligned}

Ordine di reazione

ordine di reazione

La costante $α$ è detta ordine di reazione delle [[#Cinetiche di ordine alpha]]

Costante di velocità

costante di velocità ($k_{(\alpha)}$)

La costante $k_{(α)}$ è detta costante di velocità delle [[#Cinetiche di ordine alpha]]
Ha unità di misura diverse a seconda dei valori di $α$ .

Le unità di misura della costante di velocità dipende dall'[[#Ordine di reazione]]:

\begin{aligned} α & = 0 & r_{A} & = - k_{(0)} C_{A}^{0} = - k_{(0)} & k_{(0)} & = [\begin{array}{c} \frac{m o l}{l \cdot s} \end{array}] \\ α & = 1 & r_{A} & = - k_{(1)} C_{A} & k_{(1)} & = [\begin{array}{c} \frac{1}{s} \end{array}] \\ α & = 2 & r_{A} & = - k_{(2)} C_{A}^{2} & k_{(2)} & = [\begin{array}{c} \frac{l}{m o l \cdot s} \end{array}] \end{aligned}

Cinetiche di saturazione

cinetiche di saturazione

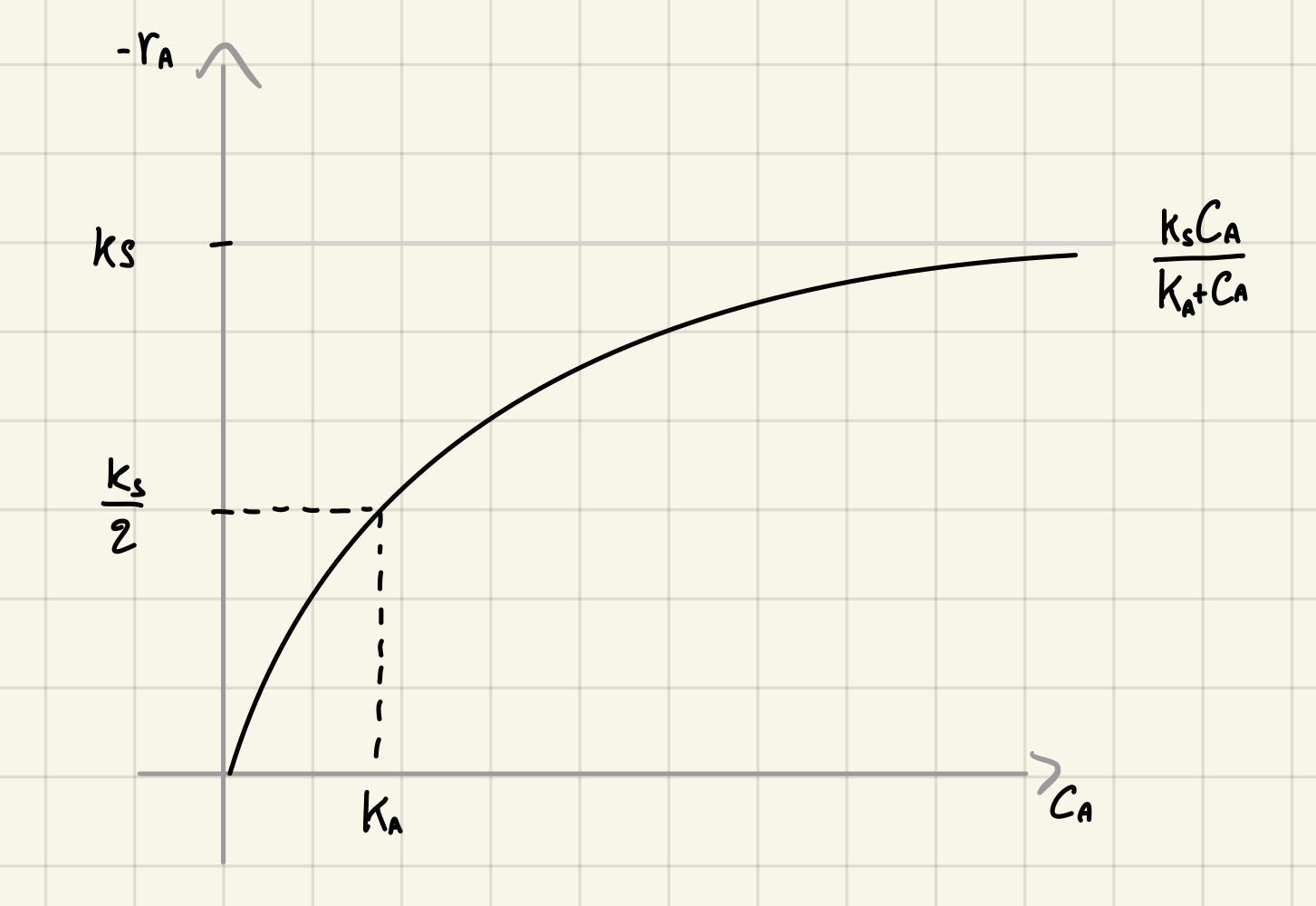
IMG_C270AAADD05C-1.jpeg|Andamento di una cinetica di saturazione
$r_{A} = - \frac{k_{s} C_{A}}{K_{A} + C_{A}}$
Dove:

$k_{s} =$ Costante di velocità
$K_{A} =$ [[#Costante di semi-saturazione]]

Le cinetiche di saturazione hanno un andamento asintotico a un valore di velocità pari proprio alla [[#Costante di velocità]] $k_{s}$ .

Nel caso delle cinetiche di saturazione è possibile semplificare la relazione funzionale attraverso delle opportune approssimazioni.
Dato

r_{A} = - \frac{k_{s} C_{A}}{K_{A} + C_{A}}

$K_{A} ≪ C_{A} ⟹ r_{A} ≃ - k_{s}$ : Ricorda una Cinetica di ordine 0
$K_{A} ≫ C_{A} ⟹ r_{A} ≃ - \frac{k_{s}}{K_{A}} C_{A}$ : Ricorda una Cinetica di ordine 1

Durante una reazione, mi aspetto che la concentrazione di $A$ diminuisca e che diminuisca quindi anche la #Velocità di reazione.

Costante di velocità (saturazione)

<-- #Cinetiche di saturazione

costante di velocità ($k_{s}$)

La costante di velocità ( $k_{s}$ ) rappresenta la velocità massima di reazione delle #Cinetiche di saturazione.

LA costante di velocità ha le dimensioni di una #Velocità di reazione:

[k_{s}] = [\frac{m o l}{l \cdot s}]

Costante di semi-saturazione

<-- [[#Cinetiche di saturazione]]

costante di semi-saturazione ($k_{a}$)

La costante di semi-saturazione (o di mezza velocità) rappresenta la [[#Concentrazione Molare]] in corrispondenza della quale la [[#Velocità di reazione]] è pari alla metà del suo valore massimo (ossia la [[#Costante di velocità (saturazione)]])

La costante di semi-saturazione ha le dimensioni di una concentrazione:

[C_{A}] = [\frac{m o l}{l}]

Reattore di Batch

reattore di batch

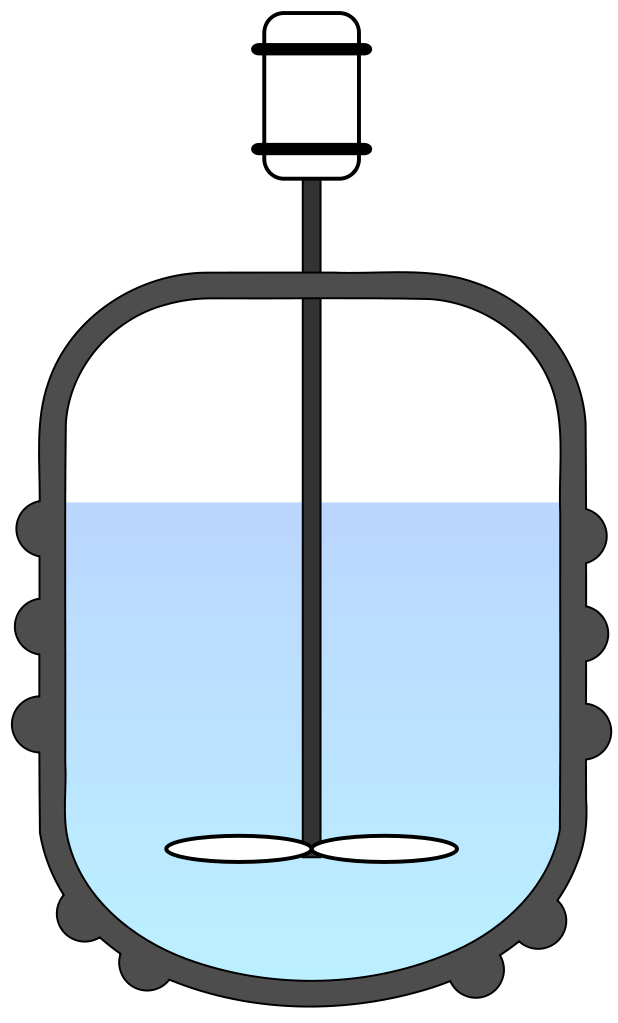
kisspng-chemical-reactor-continuous-stirred-tank-reactor-p-filebatch-reactor-str-svg-wikimedia-commons-5badde9f2c1fa0.3912803515381213751807.png|Reattore di Batch|200
Il reattore di batch, detto anche reattore discontinuo ideale è

Un reattore
Discontinuo: dopo aver avviato la reazione procede tutto autonomamente
Ideale: Le condizioni sono perfettamente omogenee (il composto è miscelato)

in cui inserisco il reagente tutto insieme, poi non faccio più nulla.

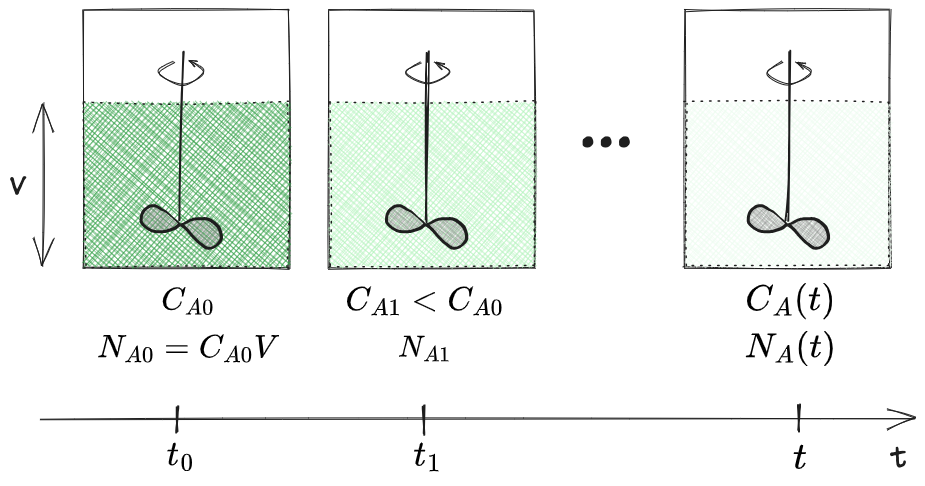
Principio di conservazione della massa

teorema

$\begin{aligned} Massa di A consumata per reazione & = Massa di A sottratta dal reattore \\ r_{A} V & = \frac{d C_{A}}{d t} V \end{aligned}$

Ci sono due modi di descrivere il reattore:

#Approccio integrale
#Approccio differenziale

Approccio integrale

Vediamo le varie cinetiche con l'approccio integrale:

#Cinetica di ordine 0 - integrale
#Cinetica di ordine 1 - integrale
#Cinetica di ordine 2 - integrale
#Cinetica di saturazione - integrale

Cinetica di ordine 0 - integrale

\frac{d C_{A} (t)}{d t} = - k_{(0)}

Integro

\int_{C_{A 0}}^{C_{A} (t)} d C_{A} (t) = \int_{0}^{t} - k_{(0)} d t

Da cui ottengo:

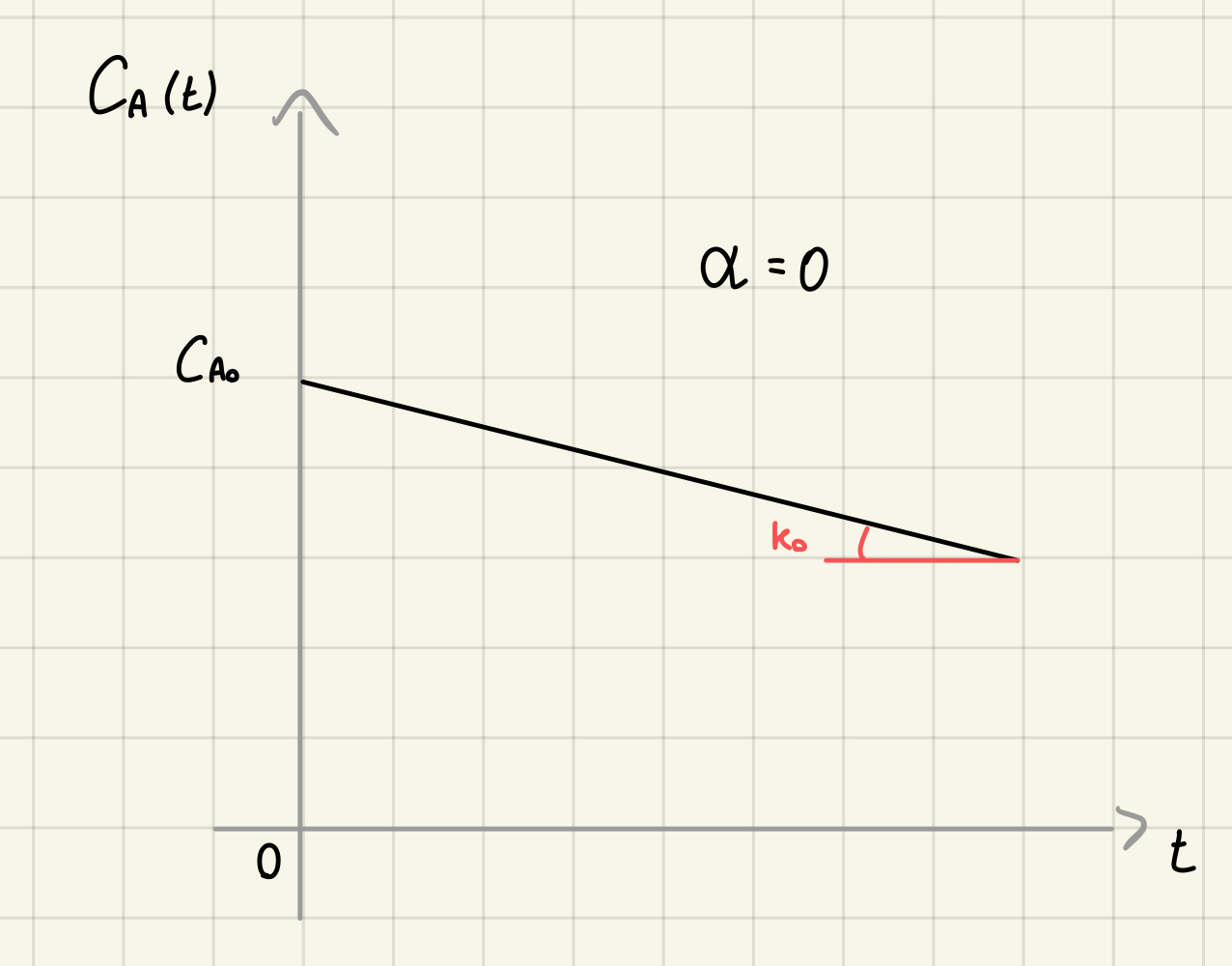
cinetica di ordine 0 - integrale - linearizzata

$C_{A} (t) = C_{A 0} - k_{(0)} t$

Cinetica di ordine 1 - integrale

\frac{d C_{A} (t)}{d t} = - k_{(1)} C_{A} (t)

Integro

\int_{C_{A 0}}^{C_{A} (t)} \frac{d C_{A} (t)}{C_{A} (t)} = - k_{(1)} \int_{0}^{t} d t

Da cui ottengo

\ln (\frac{C_{A} (t)}{C_{A_{0}}}) = - k_{(1)} t

e quindi:

cinetica di ordine 1 - integrale

$C_{A} (t) = C_{A_{0}} e^{- k_{(1)} t}$

osservazione

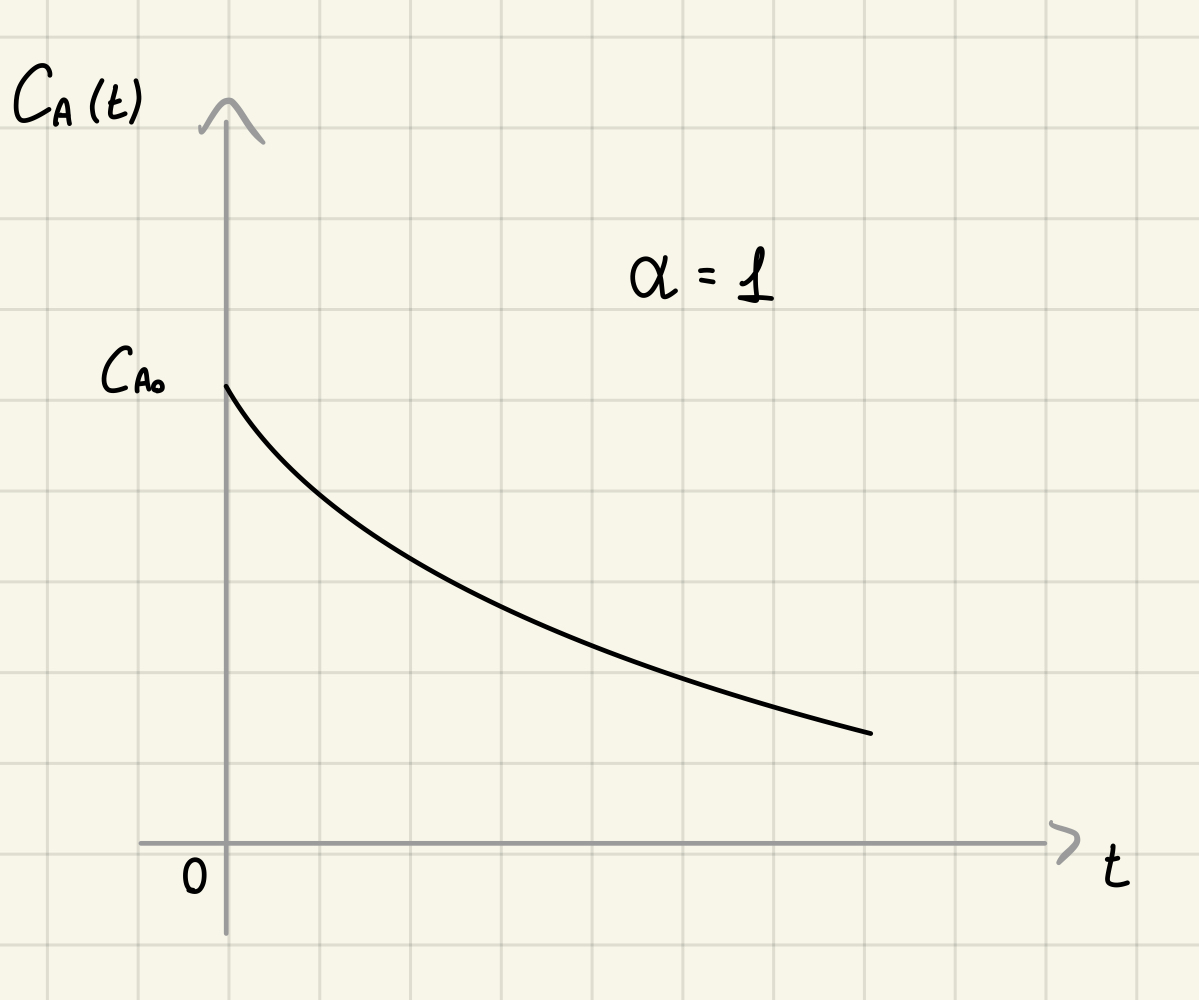
Come vedremo in seguito, conviene sempre tentare di linearizzare la relazione, graficandola su un piano diverso:

Cinetica di ordine 1 - linearizzazione

Applico il $\ln$ a entrambi i membri:

cinetica di ordine 1 - integrale - linearizzata

$\ln (C_{A} (t)) = \ln (C_{A_{0}}) - k_{(1)} t$

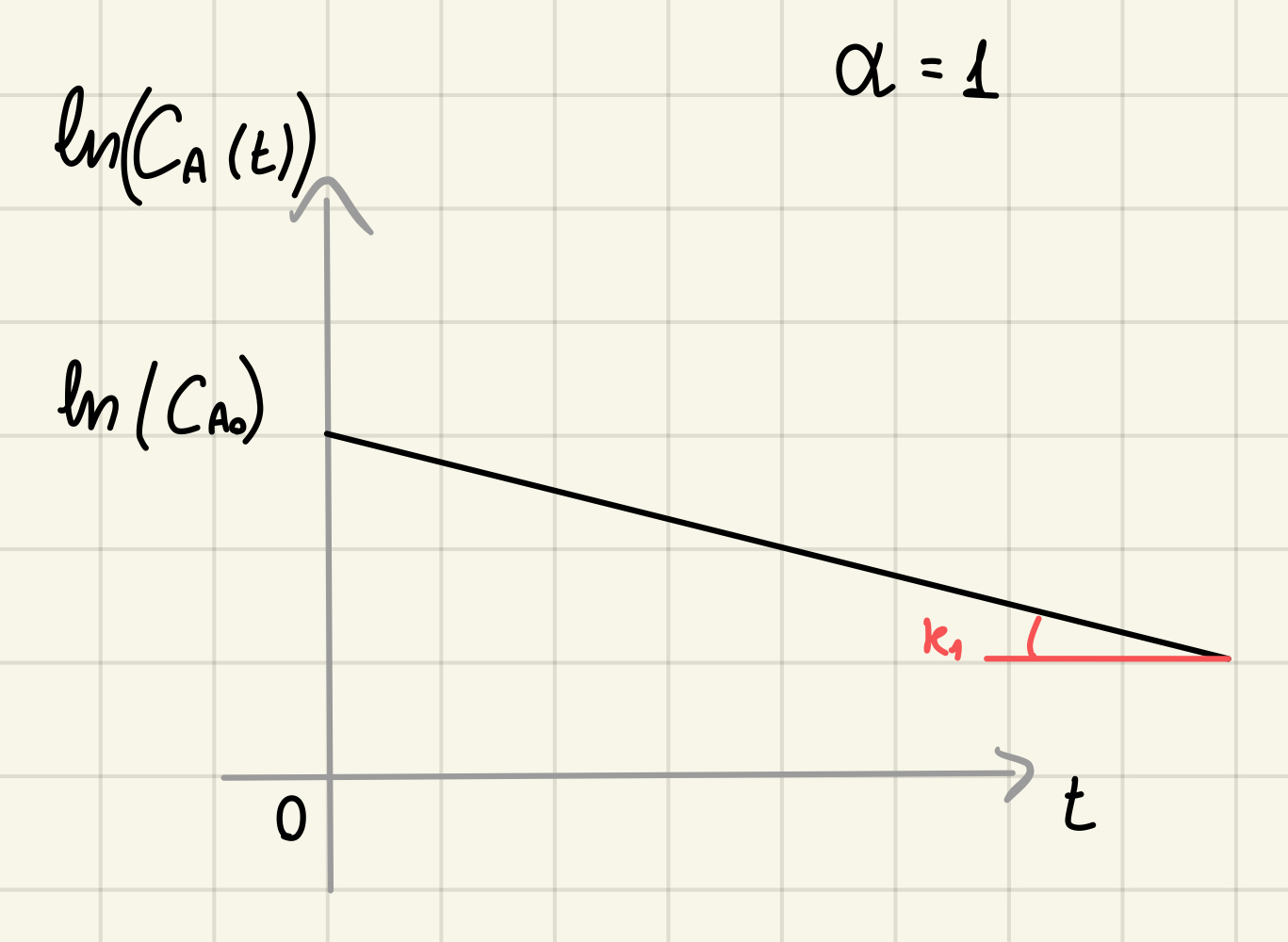
In questo modo abbiamo di nuovo una relazione in cui l'unico parametri è $k_{1}$ come coefficiente della retta.

Cinetica di ordine 2 - integrale

\frac{d C_{A} (t)}{d t} = - k_{(2)} C_{A}^{2} (t)

Integro

\int_{C_{A 0}}^{C_{A} (t)} \frac{d C_{A} (t)}{C_{A}^{2} (t)} = - k_{(2)} \int_{0}^{t} d t

Da cui ottengo

- \frac{1}{C_{A} (t)} + \frac{1}{C_{A_{0}}} = - k_{(2)} t

che linearizzando diventa:

cinetica di ordine 2 - integrale - linearizzarta

$\frac{1}{C_{A} (t)} = \frac{1}{C_{A_{0}}} + k_{(2)} t$

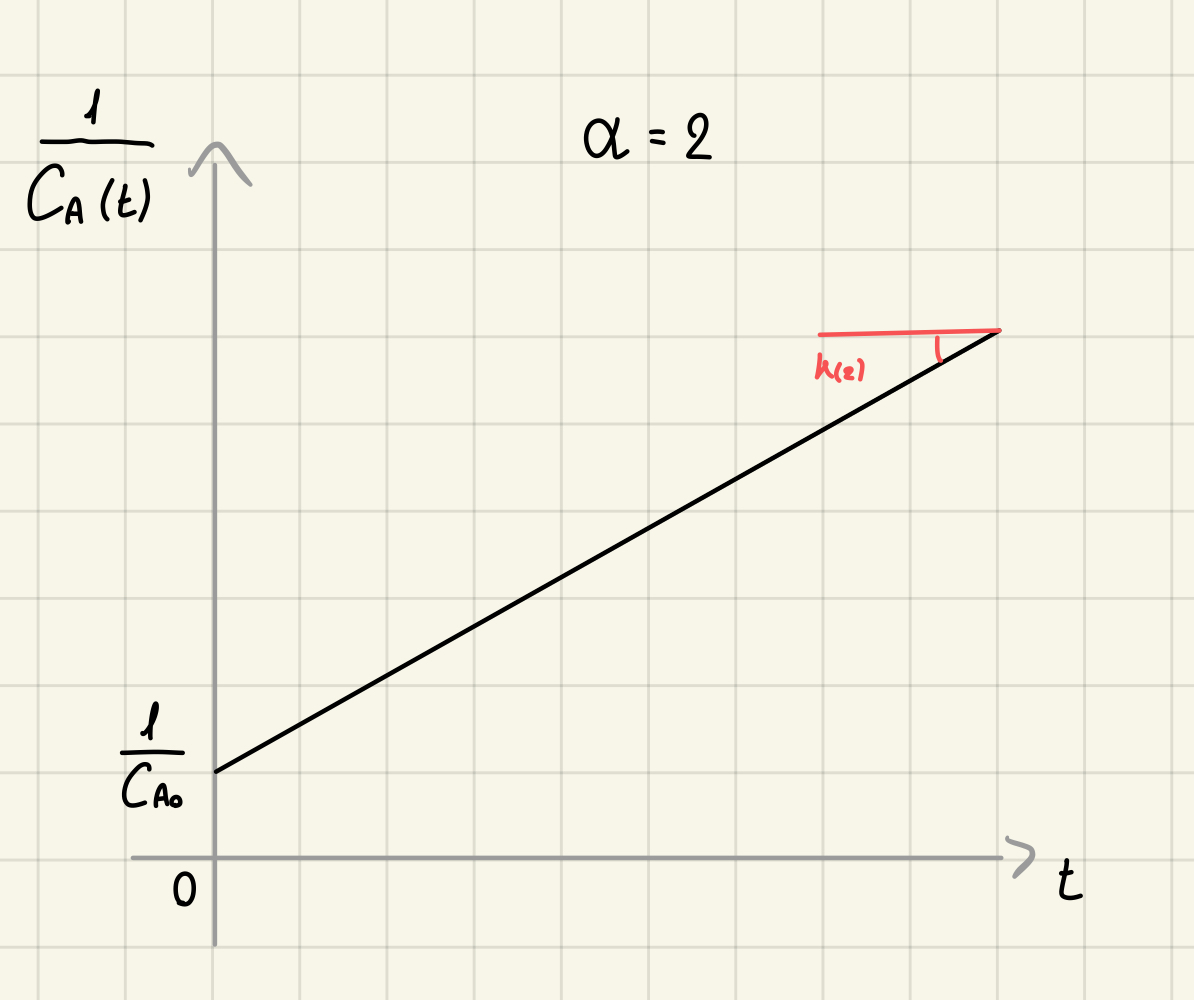
Cinetica di saturazione - integrale

Per le cinetiche di saturazione invece:

\begin{aligned} \frac{d C_{A}}{d t} & = - \frac{k_{s} C_{A} (t)}{K_{A} + C_{A} (t)} \\ \int_{C_{A_{0}}}^{C_{A} (t)} \frac{K_{A} + C_{A}}{C_{A}} d C_{A} & = - k_{s} \int_{0}^{t} d t \\ - \frac{1}{t} (K_{A} \ln (\frac{C_{A} (t)}{C_{A_{0}}}) + C_{A} (t) - C_{A_{0}}) & = - k_{s} t \frac{1}{t} (- 1) \\ \frac{1}{K_{A}} (K_{A} \frac{1}{t} \ln (\frac{C_{A_{0}}}{C_{A} (t)}) + \frac{C_{A_{0}} - C_{A} (t)}{t}) & = k_{s} \frac{1}{K_{A}} \end{aligned}

da cui ottengo, linearizzato:

cinetica di saturazione - integrale - linearizzata

$\frac{1}{t} \ln (\frac{C_{A_{0}}}{C_{A} (t)}) = \frac{k_{s}}{K_{A}} - \frac{1}{K_{A}} \frac{C_{A_{0}} - C_{A} (t)}{t}$

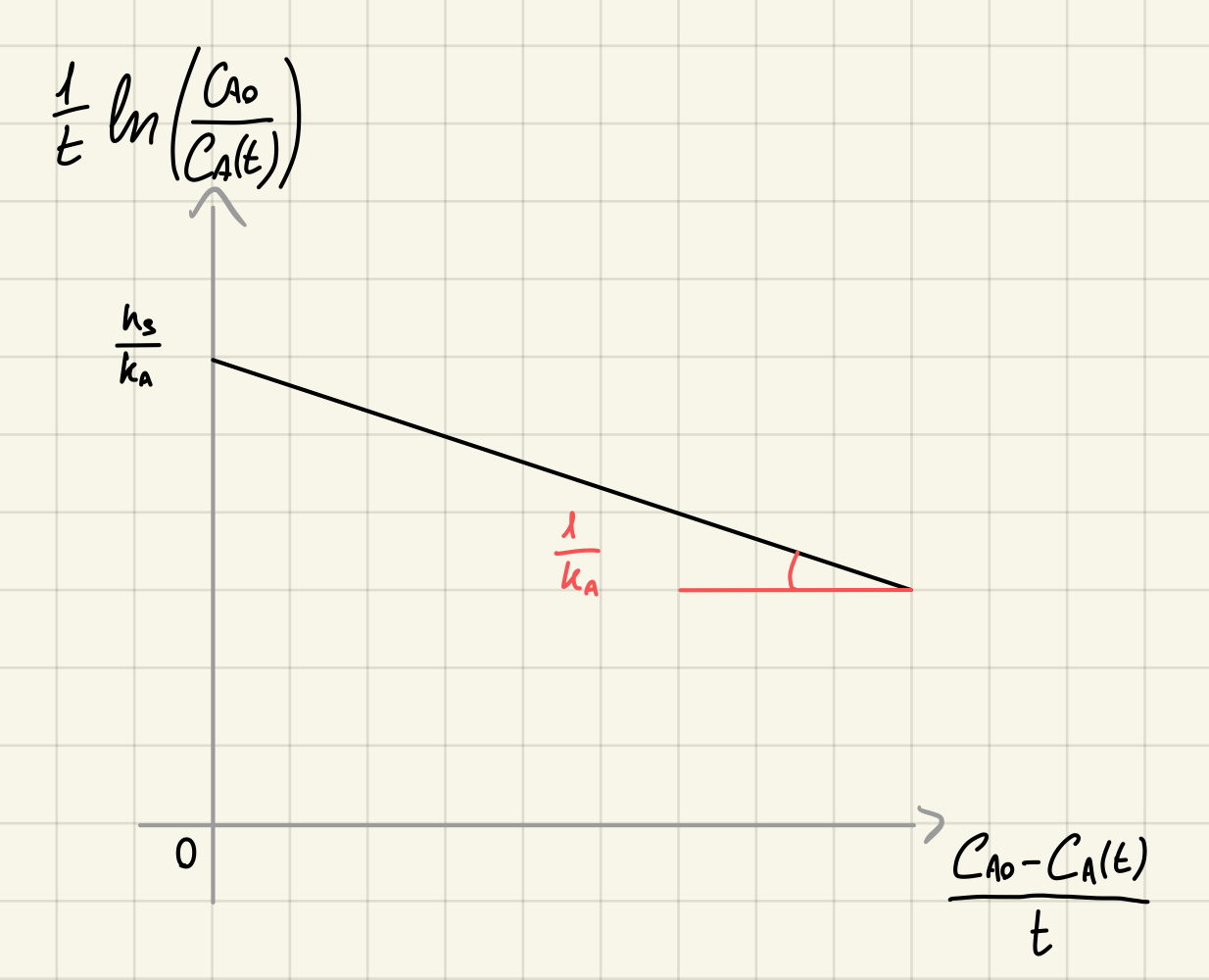
Confronto tra cinetiche linearizzate

Avere le cinetiche linearizzate, permette di confrontarle tutte graficamente.
A partire dai dati che si hanno a disposizione, si cerca su quale piano questi dati possono essere approssimati da una retta. A questo punto potremo associare al piano una delle 4 cinetiche capendo con che tipo di cinetica abbiamo a che fare.

Un'applicazione è mostrata e sviluppata in Es 1 - Determinazione dell'ordine di una reazione chimica - ISA.

Generalità sull'approssimazione

Per approssimare i dati si sfrutta la retta di regressione, un metodo di approssimazione ai minimi quadrati.

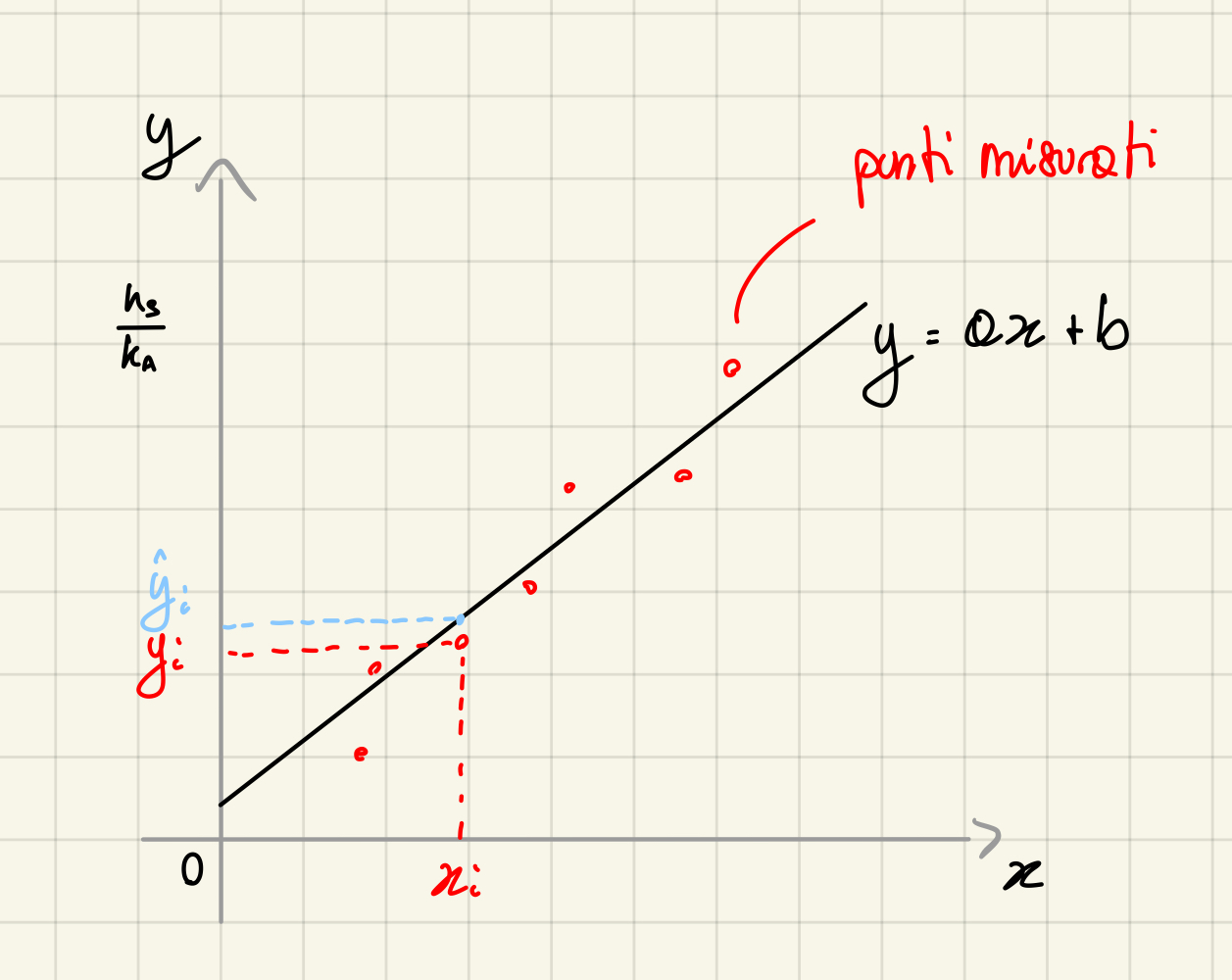
Coefficiente di determinazione

Ci chiediamo quanto la retta di regressione approssimi correttamente l'andamento reale dei dati. Possiamo definire quindi un numero, il coefficiente di determinazione $R^{2}$ , che ci da una misura di ciò.

Si definisce come segue:

R^{2} = 1 - \frac{S S E}{S S T}

dove

\begin{aligned} SSE & = \sum_{i} (y_{i} - {\hat{y}}_{i})^{2} \\ SST & = \sum_{i} (y_{i} - {\overset{―}{y}}_{i})^{2} \end{aligned}

con ${\overset{―}{y}}_{i} =$ valore medio.

Più $R^{2}$ è vicino a 1, migliore è l'approssimazione.

Approccio differenziale

\frac{d C_{A}}{d t} = r_{A}

Cinetiche di ordine alpha - differenziale

\begin{aligned} - \frac{C_{A}}{d t} & = + k_{(α)} C_{A}^{α} \\ \ln (- \frac{d C_{A}}{d t}) & = \ln k_{(α)} + α \ln C_{A} \end{aligned}

Che è già in una forma linearizzata.

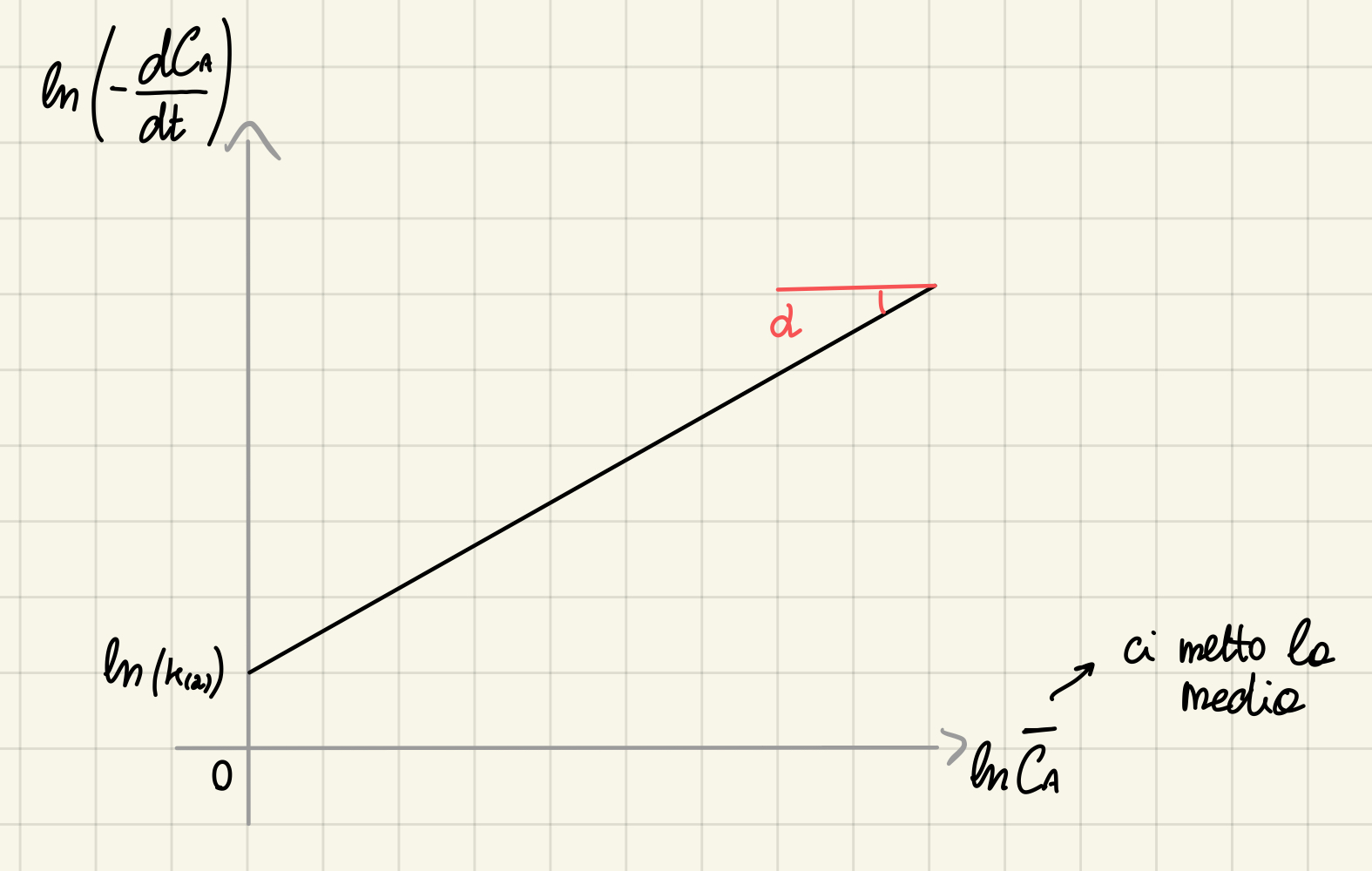
Siccome lavoro con un numero finito di punti discreti, non posso conoscere la derivata. Per questo motivo userò il rapporto incrementale:

\frac{Δ C_{A}}{Δ t}

e al posto di $C_{A}$ userò la media dell'intervallo in cui calcolo il rapporto incrementale: ${\overset{―}{C}}_{A}$

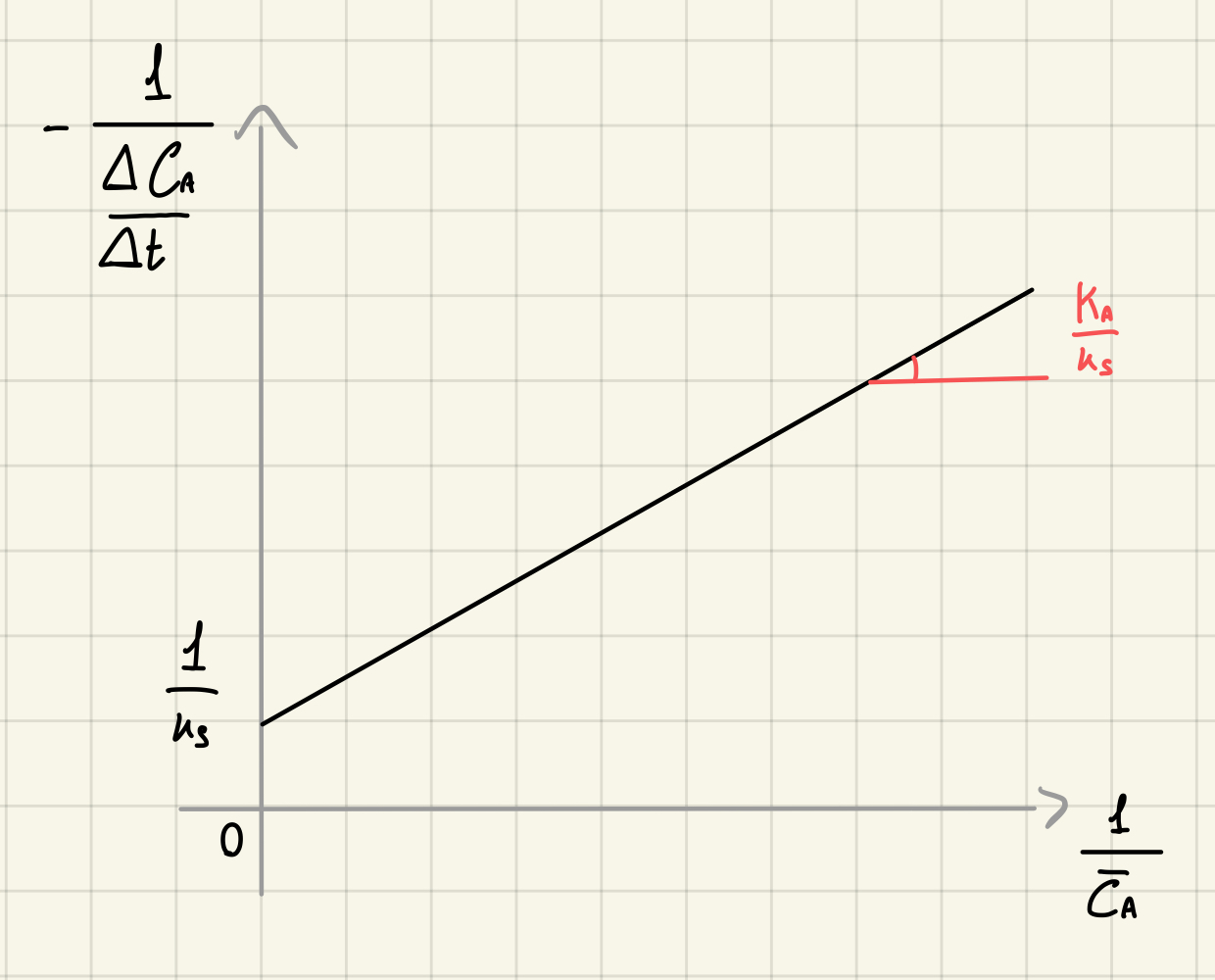
Cinetiche di saturazione - differenziale

A partire dalla relazione differenziale:

- \frac{d C_{A}}{d t} = \frac{k_{s} C_{A}}{K_{A} + C_{A}}

Posso linearizzare ottenendo:

cinetica di saturazione - differenziale - linearizzata

$- \frac{1}{\frac{d C_{A}}{d t}} = \frac{K_{A} + C_{A}}{k_{s} C_{A}} = \frac{K_{A}}{k_{s}} \frac{1}{C_{A}} + \frac{1}{k_{s}}$

Influenza della temperatura

Equazione di Vant'Hoff-Arrheius

equazione di vant'hoff-arrheius

La dipendenza della velocità di reazione dalla temperatura è data dall'equazione di Vant'Hoff-Arrheius:
$\frac{d \ln k}{d T} = \frac{E}{R T^{2}}$
dove:

$k =$ Costante di velocità della generica reazione
$T =$ Temperatura
$E =$ Energia di attivazione caratteristica della reazione considerata
$R = 8, 314 \frac{J}{m o l k}$ Costante universale dei gas perfetti

Poiché la temperatura è variabile durante una reazione, devo integrare l'equazione di Arrheius per separazione di variabili

\int_{\ln (k (T_{1}))}^{\ln (k (T_{2}))} d \ln (k) = \frac{E}{R} \int_{T_{1}}^{T_{2}} \frac{d T}{T^{2}}

da cui otteniamo:

\ln \frac{k (T_{2})}{k (T_{1})} = \frac{E}{R} (\frac{1}{T_{1}} - \frac{1}{T_{2}}) = \frac{E}{R} \frac{T_{2} - T_{1}}{T_{1} T_{2}}

Consideriamo un campo di temperatura tale per cui possiamo considerare costante il prodotto $T_{1} T_{2} = c o s t$ .
Si può riscrivere l'equazione come

\begin{aligned} \frac{k (T_{2})}{k (T_{1})} & = e^{c o s t \cdot (T_{2} - T_{1})} \\ k (T_{2}) & = k (T_{1}) θ e^{T_{2} - T_{1}} \end{aligned}