03. Processi di Consolidazione

08. Processi di Consolidazione

L'applicazione di una perturbazione (un carico o scarico) al terreno causa l'insorgere di sovrappressioni interstiziali la cui intensità è generalmente variabile da punto a punto - se in condizioni non drenate.

La condizione delle $u$ non è più in equilibrio con le condizioni idrauliche al contorno e si instaura pertanto un moto di filtrazione.

Nei terreni a grana fine, che lavorano, salvo tempi di applicazione della perturbazione particolarmente esteri, in condizioni non drenate, si instaurano i suddetti moti di filtrazione e si ha un incremento delle pressioni interstiziali. Si avranno deformazioni volumetriche nulle ( $ε_{v} = 0$ )
Si ricorda che in queste condizioni

Δ σ = Δ u

Condizioni edometriche
Condizioni Isotrope

Nei terreni a grana grossa di contro, lavorando in condizioni drenate, non si generano sovrappressioni interstiziali e tutto il carico si distribuisce sulle tensioni efficaci.

La durata del fenomeno dipende da:

Permeabilità del terreno
Deformabilità dello scheletro solido
Geometria del problema
Condizioni al contorno

processo di consolidazione

Si definisce processo di consolidazione il complesso dei fenomeni che si instaurano dall'applicazione della perturbazione in condizioni non drenate, al raggiungimento delle condizioni drenate.

È importante perché:

resistenza al taglio dipende dalle tensioni efficaci
Anche i cedimenti dipendono dalle tensioni efficaci quindi non si sviluppano subito ma solo a lungo termine

La teoria della consolidazione

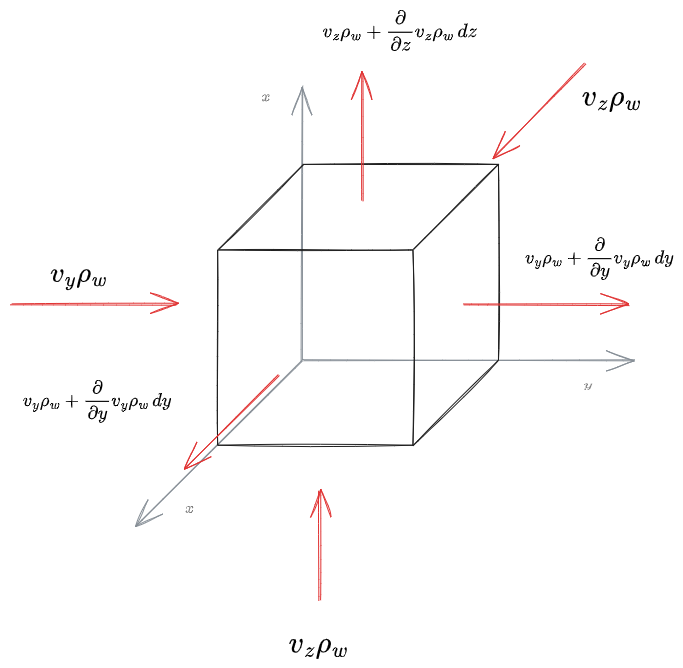
Si considera un volume elementare di terreno $d x d y d z$ e si scrive il bilancio della massa che entra ed esce da tale volume.

Si avrà in ingresso una portata in massa $v_{i} ρ_{w}$ e in uscita $v_{i} ρ_{i} + \frac{\partial v_{i}}{\partial x_{i}} ρ_{w} d x_{i}$ nella generica direzione i. Considerando positivi i contributi entranti e negativi quelli uscenti e sommando i contributi nelle tre direzioni moltiplicati per la superficie di ingresso o uscita si ottiene (considerando $ρ_{w}$ costante nel secondo passaggio):

\begin{aligned} - [\frac{\partial (v_{x} ρ_{w})}{\partial x} + \frac{\partial (v_{y} ρ_{w})}{\partial y} + \frac{\partial (v_{z} ρ_{w})}{\partial z}] \underset{d V}{\underset{⏟}{d x d y d z}} & = - \frac{\partial m_{w}}{\partial t} \\ - \vec{\nabla} \cdot \vec{v} ρ_{w} d V = - \frac{\partial m_{w}}{\partial t} \end{aligned}

La variazione di massa di fluido può essere scritta anche come:

\frac{\partial m_{w}}{\partial t} = \frac{\partial}{\partial t} (ρ_{w} \frac{S_{r} e}{1 + e} d x d y d z)

Essendo:

$S_{r} =$ grado di saturazione
$e =$ indice dei vuoti

si ricorda, essendo $S_{r} = \frac{V_{w}}{V_{v}}$
$d m_{w} = ρ_{w} d V_{w} = ρ_{w} S_{r} d V_{v}$
Inoltre, ricordando la definizione di indice dei vuoti $e = \frac{V_{v}}{V_{s}}$
$\begin{aligned} d V_{v} & = e d V_{s} = \\ = e (d V - d V_{v}) \end{aligned}$
per cui
$d V_{v} (1 + e) = e d V$
e quindi
$d V_{v} = \frac{e}{1 + e} d V$
da questo deriva che
$\begin{array}{r} \frac{d m_{w}}{d t} = \frac{d (ρ_{w} S_{r} d V_{v})}{d t} = \frac{d}{d t} (ρ_{w} S_{r} \frac{e}{e + 1}) \end{array}$

Ricordando la relazione

\frac{d V}{1 + e} = \frac{d V}{\frac{d V_{s} + d V_{v}}{d V_{s}}} = d V_{s}

possiamo scrivere

\begin{aligned} \frac{\partial m_{w}}{\partial t} & = \frac{\partial}{\partial t} (ρ_{w} \frac{S_{r} e}{1 + e} d x d y d z) \\ = \frac{d V}{1 + e} \frac{\partial}{\partial t} (ρ_{w} S_{r} e) = \\ = \frac{d V}{1 + e} (\frac{\partial ρ_{w}}{\partial t} S_{r} e + ρ_{w} \frac{\partial S_{r}}{\partial t} e + ρ_{w} S_{r} \frac{\partial e}{\partial t}) \end{aligned}

Considerando $S_{r} = c o s t = 1$ (terreno è e rimane saturo) e $ρ_{w} = c o s t$ (acqua è incomprimibile), la relazione sopra diventa:

\begin{aligned} \frac{\partial m_{w}}{\partial t} & = \frac{d V}{1 + e} ρ_{w} \frac{\partial e}{\partial t} = \\ = ρ_{w} \frac{d V}{d t} \frac{d e}{1 + e} \end{aligned}

che, essendo $\frac{d e}{1 + e} = d ε_{v}$ diventa

\frac{d m_{w}}{d t} = ρ_{w} d V \frac{\partial ε_{v}}{\partial t}

Uguagliando alla prima relazione trovata:

\frac{d m_{w}}{d t} = ρ_{w} d V \frac{\partial ε_{v}}{\partial t} = \vec{\nabla} \cdot \vec{v} ρ_{w} d V

e quindi

\frac{\partial ε_{v}}{\partial t} = \vec{\nabla} \cdot \vec{v}

Assumendo la validità della legge di D'Arcy ( $\vec{v} = - k \vec{\nabla h}$ ) si può scrivere

\begin{aligned} \frac{\partial ε_{v}}{\partial t} & = \vec{\nabla} \cdot (- k \vec{\nabla h}) = \\ = - k \nabla^{2} h \end{aligned}

Il carico idraulico dipende esclusivamente dalle sovrappressioni interstiziali $\frac{\overset{―}{u}}{γ_{w}}$

\frac{\partial ε_{v}}{\partial t} = - k \nabla^{2} (\frac{\overset{―}{u}}{γ_{w}})

che diventa:

\frac{\partial ε_{v}}{\partial t} = - \frac{k}{γ_{w}} \nabla^{2} \overset{―}{u}

Ipotizzando il comportamento elastico lineare isotropo del terreno, la deformazione volumetrica si può riscrivere come

ε_{v} = \frac{\overset{―}{p^{'}}}{K} = \frac{\overset{―}{p} - \overset{―}{u}}{K}

(essendo K il modulo di compressibilità volumetrica)
e quindi la relazione di prima diventa:

equazione di biot

$\frac{\partial \overset{―}{p}}{\partial t} - \frac{\partial \overset{―}{u}}{\partial t} = - \frac{k \cdot K}{γ_{w}} \nabla^{2} \overset{―}{u}$

che è un'equazione differenziale del II ordine detta #Equazione di Biot
Questa equazione da sola non basta a risolvere il problema; bisogna associare le Equazioni indefinite dell'equilibrio.

ipotesi

Incompressibilità dei granuli solidi $\frac{\partial}{\partial t} (\frac{d V}{1 + e}) = \frac{\partial V_{s}}{\partial t} = 0$
Incompressibilità della fase liquida $ρ_{w} = c o s t$
Saturazione del terreno $S_{r} = 1$
Comportamento elastico lineare dello scheletro solido $ε_{v} = \frac{d \overset{―}{p^{'}}}{K}$ con $K = c o s t$
Validità della legge di D'Arcy generalizzata $\vec{v} = k \vec{\nabla h}$
Isotropia e omogeneità della permeabilità e permeabilità costante durante la consolidazione $k_{x} = k_{y} = k_{z} = c o s t$

Teoria della consolidazione monodimensionale di Terzaghi

Si analizza il caso particolare in cui la consolidazione è monodimensionale.
Quindi:

\nabla^{2} \overset{―}{u} = \frac{\partial^{2} \overset{―}{u}}{\partial z^{2}} ε_{v} = \frac{\overset{―}{σ_{z}^{'}}}{E_{e d}} = \frac{\overset{―}{σ_{z}} - \overset{―}{u}}{E_{e d}}

dove:

$E_{e d} =$ Rigidezza
$\overset{―}{σ_{z}^{'}}, \overset{―}{σ_{z}} =$ Variazioni di tensione efficaci e totale in direzione $z$

Sotto queste ipotesi, l'equazione

- \frac{k}{γ_{w}} \nabla^{2} \overset{―}{u} = \frac{\partial ε_{v}}{\partial t}

diventa:

\frac{E_{e d} k}{γ_{w}} \frac{\partial^{2} \overset{―}{u}}{\partial z^{2}} = \frac{\partial \overset{―}{u}}{\partial t} - \frac{\partial \overset{―}{σ_{z}}}{\partial t}

Definendo il #Coefficiente di consolidazione $c_{v} = \frac{E_{e d} k}{γ_{w}}$ , e supponendo che la tensione totale vari istantaneamente all'inizio del processo e rimanga poi costante, si può scrivere:

equazione di terzaghi

$c_{v} \frac{\partial^{2} \overset{―}{u}}{\partial z^{2}} = \frac{\partial \overset{―}{u}}{\partial t}$

ipotesi

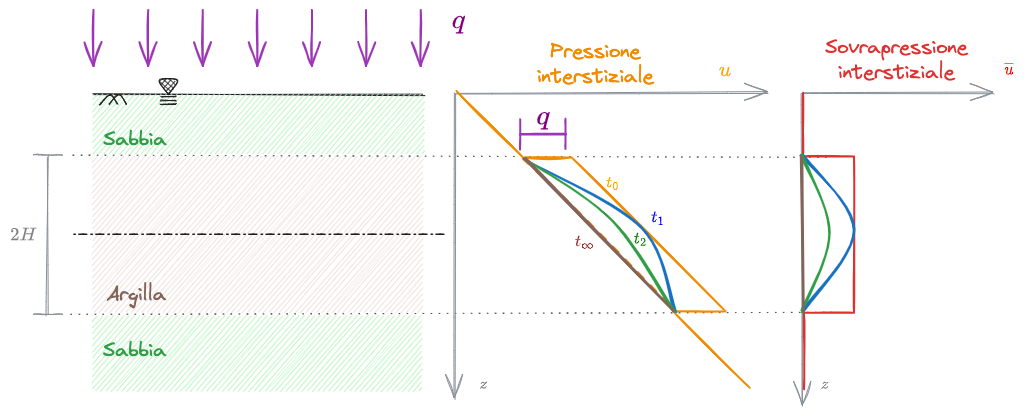
Oltre alle ipotesi valide per l'[[#Equazione di Biot]], l'Equazione di Terzaghi richiede anche queste altre ipotesi:

Flusso monodimensionale - $v_{x} = v_{y} = 0$
Deformazioni monodimensionali - $ε_{v} = ε_{z}$
La perturbazione è applicata istantaneamente e tenuta costante nel tempo - $\overset{―}{σ_{z}} = c o s t$

È utile riscrivere le equazioni trovate in forma adimensionale. Si definiscono quindi le seguenti grandezze:

$H =$ #Altezza di drenaggio
$Z =$ #Profondità normalizzata
$T_{v} =$ #Fattore Tempo

Definiti questi valori, si può riscrivere l'equazione di Terzaghi come:

\frac{\partial^{2} \overset{―}{u}}{\partial Z^{2}} = \frac{\partial \overset{―}{u}}{\partial T_{v}}

Sia $\overset{―}{u} (z, t)$ la soluzione all'equazione di Terzaghi, si definisce il #Grado di consolidazione

Altezza di drenaggio

altezza di drenaggio ($h$)

L'altezza di drenaggio, $H$ , è la massima distanza che una particella d'acqua deve percorrere per raggiungere il contorno drenante più vicino.

Permette di definire la #Profondità normalizzata

Profondità normalizzata

profondità normalizzata ($z$)

$Z = \frac{z}{H}$

Fattore Tempo

fattore tempo ($t_{v}$)

$\frac{c_{v} T}{H^{2}}$

Grado di consolidazione

fattore di consolidazione ($u$)

Il fattore di consolidazione è il rapporto tra la sovrappressione dissipata e quella iniziale.
$U = \frac{\overset{―}{u_{0}} (z) - \overset{―}{u} (z, t)}{\overset{―}{u_{0}} (z)}$

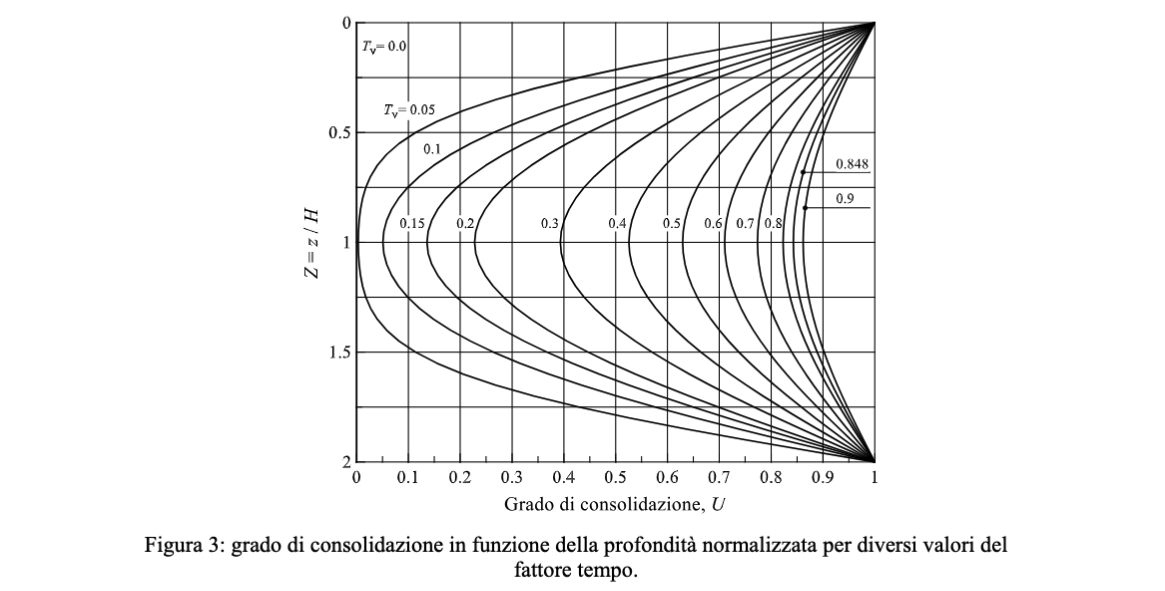
L'andamento della #Profondità normalizzata in funzione del grado di normalizzazione è mostrato nella figura sottostante. Si noti come, in prossimità dei contorni drenanti, le sovrappressioni si dissipino più rapidamente che nelle altre zone.

Si definisce anche un #Grado di consolidazione medio

Grado di consolidazione medio

grado di consolidazione medio ($\overline{u}$)

Il Grado di consolidazione medio è definito come:
$\overset{―}{U} = \frac{\int_{0}^{H} {\overset{―}{u}}_{0} (z) d x - \int_{0}^{H} \overset{―}{u} (t, z) d z}{\int_{0}^{H} {\overset{―}{u}}_{0} (z) d z}$

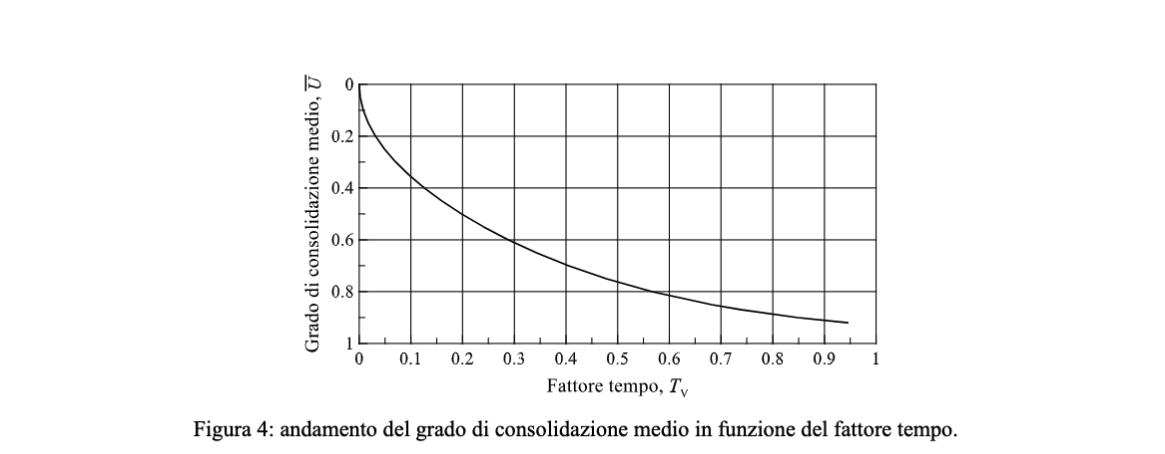
Il grado di consolidazione medio è utile in quanto può essere messo direttamente in relazione con il #Fattore Tempo mediante il grafico qui di seguito

[?] come si calcolano i cedimenti? Perché si calcolano come scritto nelle dispense?

w (t) = \frac{1}{E_{e d}} \int_{0}^{L} \overset{―}{σ_{v}^{'}} d z

Il grado di consolidazione medio può anche essere espresso in funzione dei cedimenti:

\overset{―}{U} = \frac{w (t)}{w_{f}}

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ Cos'è la roba su Casagrande?
❗❗❗❗❗❗❗❗❗❗❗❗❗

[?] Abbiamo fatto la roba su Casagrande?