02. Moti di Filtrazione

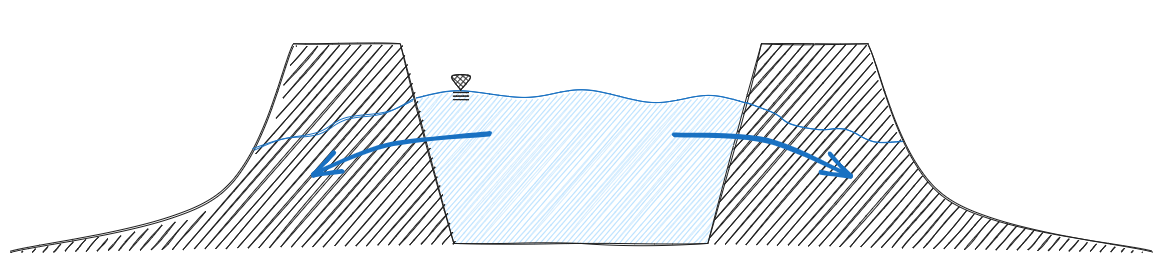
Nell'immagine sopra è mostrato un caso in cui possono verificarsi dei moti di filtrazione. In questo caso accade che l'acqua tende a filtrare attraverso gli argini.

Un caso molto comune in cui si hanno moti di filtrazione è quello degli scavi. L'acqua infatti tende a filtrare da sotto lo scavo (aggottare) e si deve quindi intervenire pompandola fuori. È importante studiare questi fenomeni perché le filtrazioni hanno effetto sulle tensioni efficaci e possono quindi portare a fenomeni di #Instabilità.

Carico idraulico

carico idraulico

Si definisce carico idraulico, e rappresenta un'energia per unità di peso, la quantità $h$ :
$h = z + \frac{u}{γ_{w}} + \frac{v^{2}}{2 g}$
dove:

$z =$ Quota geometrica
$\frac{u}{γ_{w}} =$ Altezza piezometrica
$\frac{v^{2}}{2 g} =$ Altezza cinetica
ed è una misura della quantità di energia nel mezzo.

Noi considereremo l'altezza cinetica pari a 0.

h = z + \frac{u}{γ_{w}} Quota piezometrica

Si può vedere con pochi passaggi che $h$ rappresenta di fatto un'energia:
$\begin{aligned} h & = z + \frac{u}{γ_{w}} + \frac{v^{2}}{2 g} = \\ γ_{w} g h & = γ_{w} g z + g u + \frac{1}{2} γ_{w} v^{2} \end{aligned}$
dove le unità di misura sono
$[\frac{k g}{m^{3}} \cdot \frac{m}{s^{2}} \cdot m] = [\frac{k g}{m \cdot s^{2}}]$
che corrisponde in realtà a un'energia per unità di volume:
$[\frac{k g}{m \cdot s^{2}}] = [\frac{k g \cdot m^{3}}{m \cdot s^{2}}] = [\frac{k g \cdot m^{2}}{s^{2}}] = [N \cdot m] = [J]$

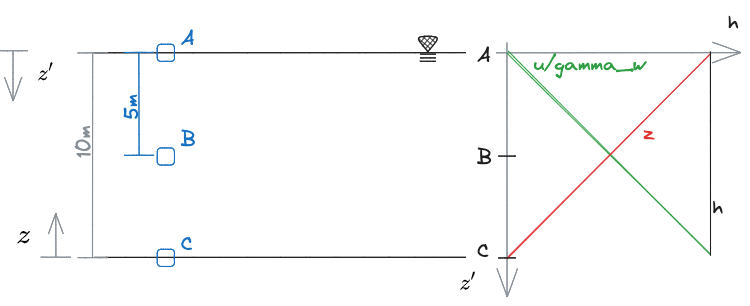
In condizioni idrostatiche, il carico idraulico si mantiene costante al variare della profondità come mostrato nell'esempio che segue

esempio

01. Moti di Filtrazione 2023-10-29 20.16.46.excalidraw.png
%%🖋 Edit in Excalidraw, and the dark exported image%%

$\begin{aligned} h_{A} & = 10 m + \frac{0}{γ_{w}} = 10 m \\ h_{B} & = 5 m + \frac{5 m \cdot γ_{w}}{γ_{w}} = 10 m \\ h_{C} & = 0 m + \frac{10 m \cdot γ_{w}}{γ_{w}} = 10 m \end{aligned}$
Si riportano gli andamenti di $z^{'}, z, \frac{u}{γ_{w}}, h$ in tabella

	$z^{'}$	$z$	$\frac{u}{γ_{w}}$	$h$
A	0	10	0	10
B	5	5	5	10
C	10	0	10	10

È evidente quindi che si ha $h$ costante lungo tutto lo strato

Legge di D'Arcy

D'Arcy ha condotto un esperimento che consisteva nel creare due serbatoi, uno a monte e uno a valle, a due carichi idraulici differenti.

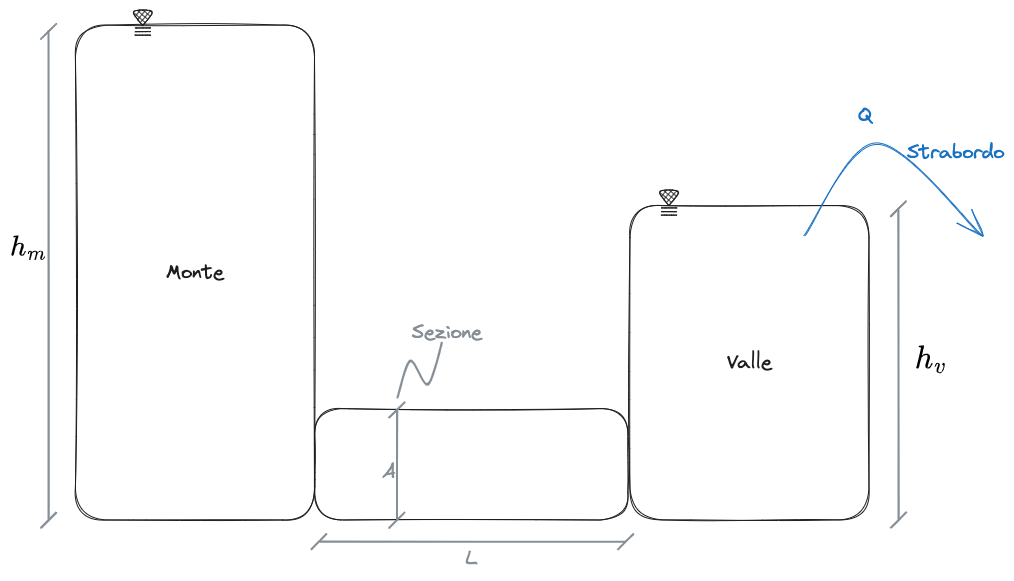
Dal serbatoio di monte, si osserva che il liquido riempie il serbatoio di valle. Il liquido deve attraversare il percorso di sezione A in cui è presente il terreno che si sta studiando. Una volta riempito il serbatoio di valle, questo inizierà a straboccare. L'acqua che fuoriesce viene misurata e da questa si può ricavare la portata del sistema, $Q$ .

La portata d'acqua è data dalla quantità di volume spostata in un certo intervallo di tempo.

\frac{Δ V}{Δ t} = Q

Questo esperimento permette di caratterizzare il materiale attraverso cui è fatta filtrare l'acqua. Infatti, se si calcola la #Velocità di filtrazione si nota essere proporzionale a un certo #Gradiente Idraul[[Università/Triennale/3° Anno/1° Semestre/Fondamenti di Geotecnica/Appunti/Moti di filtrazione/02. Moti di Filtrazione#Gradiente Idraulicoico]] secondo un coefficiente di proporzionalità che definiremo #Coefficiente di permeabilità.

Velocità di filtrazione

In riferimento all'esperimento di D'Darcy, si ricava la #Legge di D'Arcy:

v = \frac{Q}{A}

che si osserva essere uguale a

legge di darcy

$v = - k \frac{Δ h}{L}$

dove

$Δ h = h_{v} - h_{m}$
$k =$ #Coefficiente di permeabilità

La #Legge di D'Arcy può anche essere scritta in forma differenziale:

v = - k \frac{\partial h}{\partial s}

dove:

$s =$ coordinata spaziale nella direzione del moto

che si può estendere alla filtrazione generica nelle 3 dimensioni secondo la:

\vec{v} = - k \vec{\nabla h}

osservazione - $k$ non è isotropo

Nella relazione 3D si è considerato il #Coefficiente di permeabilità isotropo (uguale in tutte le direzioni), In realtà non è così.

Come sezione si è usata $A$ , l'intera sezione del canale in cui avviene la filtrazione. In realtà il fluido filtra solo attraverso i vuoti tra i grani. Pertanto la sezione risulta minore di $A$ da cui la velocità di filtrazione effettiva sarà maggiore.

Lungo il percorso di $L$ , l'energia (il #Carico idraulico) va diminuendo da $h_{m}$ a $h_{v}$ .

esempio

Alcuni valori di portata in litri orari per vari vari terreni con tutte le grandezze unitarie.

Ghiaia $k \approx 10^{- 2} \frac{m}{2} ⟹ Q_{u} = 10^{- 2} \cdot 3.6 \times 10^{3} \times 10^{3} = 3600 \frac{l}{h}$
Sabbia $k \approx 10^{- 5} \frac{m}{2} ⟹ Q_{u} = 10^{- 5} \cdot 3.6 \times 10^{3} \times 10^{3} = 36 \frac{l}{h}$
Argilla $k \approx 10^{- 10} \frac{m}{2} ⟹ Q_{u} = 10^{- 10} \cdot 3.6 \times 10^{3} \times 10^{3} = 0.00036 \frac{l}{h}$

La Legge di D'Arcy NON è applicabile a velocità di filtrazione molto elevate per via dell'instaurarsi di moti turbolenti del fluido.
Questo è il caso ad esempio delle ghiaie.

Coefficiente di permeabilità

coefficiente di permeabilità ($k$)

Nella relazione della [[#Velocità di filtrazione]], il coefficiente $k$ prende il nome di coefficiente di permeabilità.
È una misura di quanto facilmente il liquido filtra attraverso un materiale.
Un elevato valore indica un'elevata permeabilità
$k = [\frac{m}{s}]$

Dipende dalla [[Viscosità cinematica]] $ν$ :
$k = \frac{K g}{ν}$

$k$ rappresenta la portata per un #Gradiente Idraulico unitario lungo una sezione di lunghezza unitaria.

Vediamo alcuni fattori che influenzano la permeabilità:

Diametro medio dei vuoti ( $D$ ) - $k \propto D^{2}$
Indice dei vuoti ( $e$ ) - $k \propto e$ : Stato di addensamento
Liquido (viscosità)

Gradiente Idraulico

gradiente idraulico ($i$)

Nella #Legge di Darcy, la quantità
$i = \frac{Δ h}{L}$
prende il nome di gradiente idraulico.
È una misura di quanta energia viene persa, per ogni metro, nel mezzo in cui il fluido filtra.

Equazione di Laplace

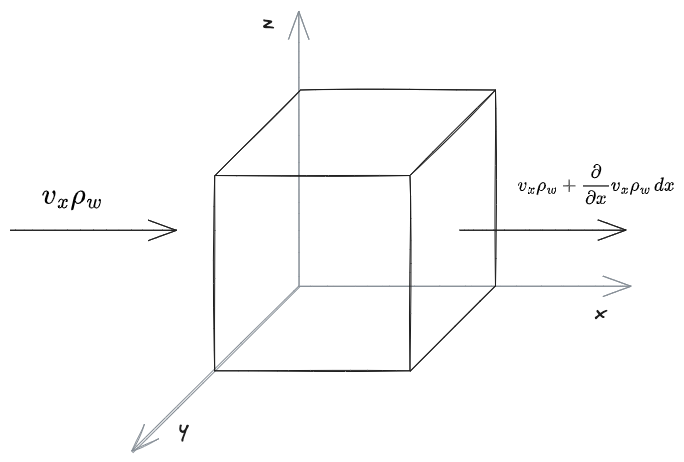
Analizziamo le portate che attraversano un generico cubo infinitesimo di lati: $d x, d y, d z$ .
Siano:

$v_{i} =$ velocità nella direzione $i$ $[\frac{m}{s}]$
$ρ_{w} =$ Densità dell'acqua $[\frac{k g}{m^{3}}]$
$v_{i} ρ_{w} =$ Portata d'acqua in direzione $i$ $[\frac{k g}{s \cdot m^{2}}]$
In ogni direzione $i$ , entrerà da una faccia una portata

v_{i} ρ_{w}

e uscirà dalla faccia opposta, a distanza $d x$

v_{i} ρ_{w} + \frac{\partial}{\partial i} v_{i} ρ_{w} d i

In ogni dimensione, se scrivessimo un bilancio di materia di ciò che entra ed esce dal cubo, avremmo:

v_{i} ρ_{w} - v_{i} ρ_{w} - \frac{\partial}{\partial i} v_{i} ρ_{w} d i = - \frac{\partial}{\partial i} v_{i} ρ_{w} d i

Che posso generalizzare in tre dimensioni, moltiplicando di volta in volta per la sezione, ottenendo:

- (\frac{\partial}{\partial x} v_{x} ρ_{w} d x d y d z + \frac{\partial}{\partial y} v_{y} ρ_{w} d y d x d z + \frac{\partial}{\partial z} v_{z} ρ_{w} d z d x d y) = \frac{\partial m_{w}}{\partial t} = 0

Nel caso stazionario con $m = c o s t$ .
L'equazione di prima si semplifica dividendo tutto per $d x d y d z$ :

\begin{array}{r} - (\frac{\partial}{\partial x} v_{x} + \frac{\partial}{\partial y} v_{y} + \frac{\partial}{\partial z} v_{z}) = 0 \\ - \vec{\nabla \cdot v} = 0 \end{array}

che è stata riscritta come divergenza della velocità.

Inserendo la [[#Legge di Darcy]] nella relazione appena trovata, e quindi ricordando che $\vec{v} = \vec{\nabla h}$ otteniamo che:

\begin{array}{r} - \vec{\nabla \cdot v} = 0 \\ - \vec{\nabla} \cdot \vec{\nabla h} = 0 \\ \vec{\nabla^{2} h} = 0 \end{array}

Si è scritta quindi l'equazione di Laplace:

equazione di laplace

$\vec{\nabla^{2} h} = 0$

Il nostro obiettivo sarà pertanto quello di risolvere l'equazione di Laplace per conoscere $h$ da cui ricavare $u$ e di conseguenza le $σ^{'}$ (tensioni efficaci).

Soluzione dell'equazione di Laplace

In realtà non è necessario risolvere l'#Equazione di Laplace in tutto il dominio. Infatti non sarà necessario risolvere l'equazione in tutte quelle zone in cui il carico idraulico rimane invariato. Si risolverà, come vedremo, esclusivamente nei limiti del #Dominio di filtrazione.

Si deve quindi determinare l'area in cui è invece necessario risolvere il problema.

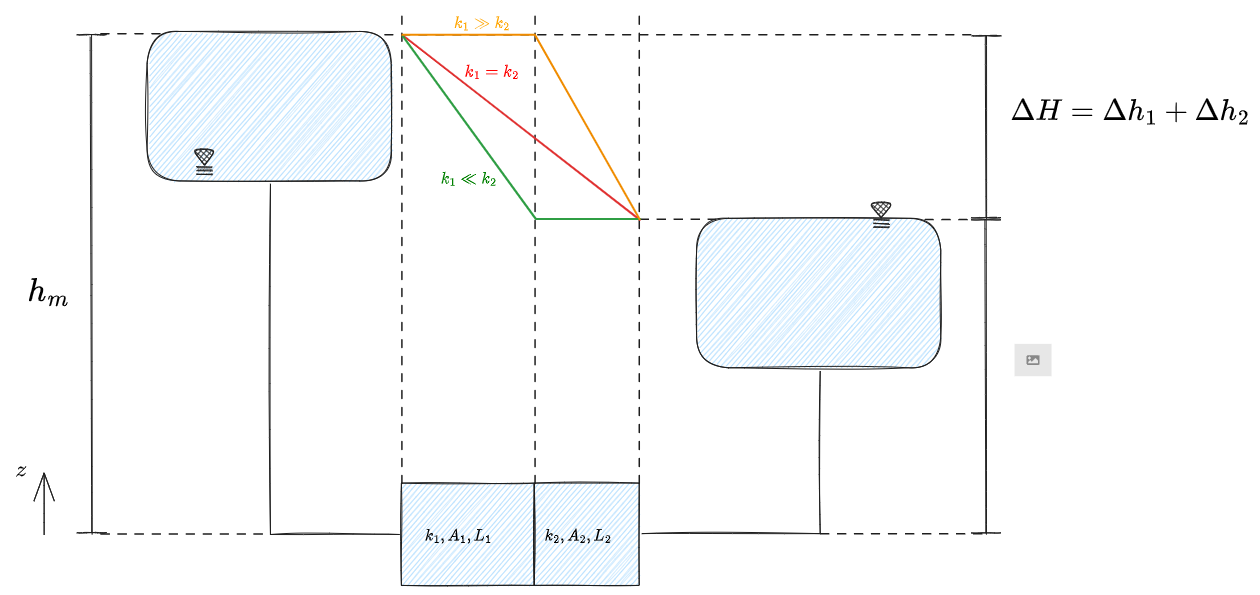
Nella figura sopra si considerano due serbatoi collegati attraverso un cilindro diviso in 2, di due materiali diversi, attraverso i quali l'acqua può filtrare.

Si dovrà verificare la condizione per cui le portate attraverso le due sezioni devono essere le stesse, quindi:

Q_{1} = Q_{2}

e la perdita di carico totale sarà data dalla somma delle perdite di carico:

Δ H = Δ h_{1} + Δ h_{2}

Sfruttando quanto detto per la #Legge di D'Arcy si può scrivere la portata come

Q = v A = k i \cdot A

quindi:

\begin{aligned} k_{1} i_{1} A_{1} & = k_{2} i_{2} A_{2} \\ k_{1} \frac{Δ h_{1}}{L_{1}} A_{1} & = k_{2} \frac{Δ h_{2}}{L_{2}} A_{2} \end{aligned}

da cui posso ricavare una delle due perdite di carico:

Δ h_{2} = Δ h_{1} \frac{k_{1}}{k_{2}} \frac{A_{1}}{A_{2}} \frac{L_{2}}{L_{1}}

Inserendo questa in $Δ H = Δ H_{1} + Δ H_{2}$
si può scrivere che:

Δ H = Δ h_{1} + Δ h_{1} \frac{k_{1}}{k_{2}} \frac{A_{1}}{A_{2}} \frac{L_{2}}{L_{1}}

e quindi

Δ h_{1} = \frac{Δ H}{1 + \frac{k_{1}}{k_{2}} \frac{A_{1}}{A_{2}} \frac{L_{2}}{L_{1}}} Δ h_{2} = \frac{Δ H}{1 + \frac{k_{2}}{k_{1}} \frac{A_{2}}{A_{1}} \frac{L_{1}}{L_{2}}}

Ora per ognuno dei parametri $k, A, L$ vedo cosa succede se 2 di loro sono uguali e il terzo sono uno molto maggiore dell'altro. Ad esempio:

A_{1} = A_{2} L_{1} = L_{2} k_{1} ≫ k_{2}

in questo caso il rapporto $\frac{k_{1}}{k_{2}} \to \infty$ e quindi $Δ H_{1} = 0$ e allora tutta la perdita di carico si ha in 2: $Δ H \approx Δ H_{2}$ .
Facendo lo stesso per ogni parametro si cerca dove si ha la maggior parte della perdita di carico e quindi di quale sia il #Dominio di filtrazione.

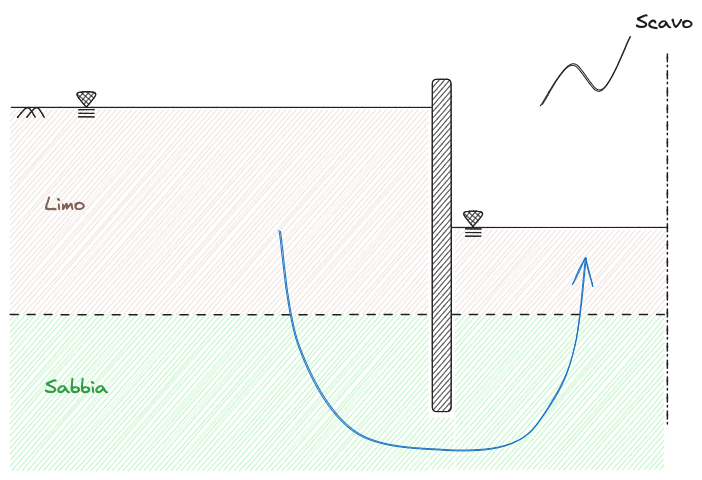
Negli scavi, in rispetto alle superfici e a parità di altre condizioni, la perdita di carico si ha sempre in corrispondenza dello scavo. Infatti, a parità di altre condizioni, l'Area del piano di campagna si può considerare infinitamente grande rispetto all'area di scavo, che invece è sempre di estensione finita.

In particolare, la maggior perdita di carico nel caso specifico si avrà nel limo dal lato dello scavo in quanto è il limo ad avere permeabilità minore.
Si definiscono così:

#Serbatoio
#Dominio di filtrazione

Si osservi che nel caso in cui il moto di filtrazione dovesse essere mono-dimensionale, l'#Equazione di Laplace si ridurrà a

\frac{\partial^{2} h}{\partial z^{2}} = 0

Altrimenti si avranno moti bidimensionali in cui il #Dominio di filtrazione è tutto il limo (nel caso sotto)

Serbatoio

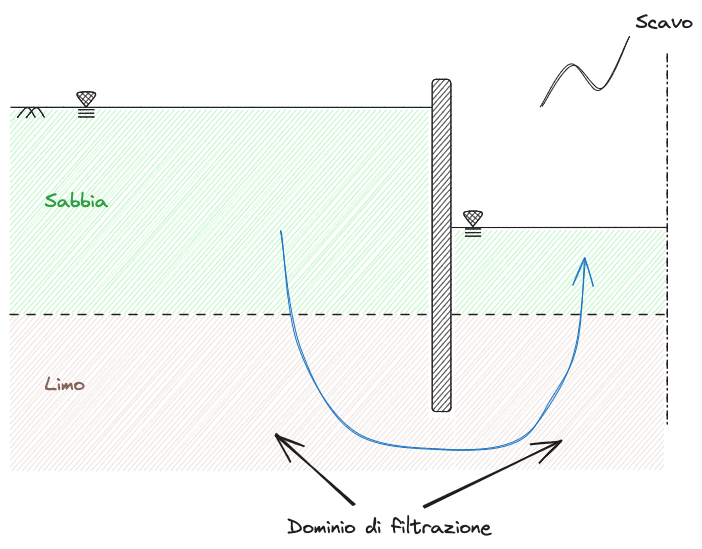
serbatoio

Per serbatoio si intende quella parte della stratigrafia nella quale l'acqua pur muovendosi non perde apprezzabilimente di carico.

Dominio di filtrazione

dominio di filtrazione (df)

L'area dove c'è filtrazione per via di un'apprezzabile perdita di carico è detta Dominio di Filtrazione

Soluzione mono-dimensionale

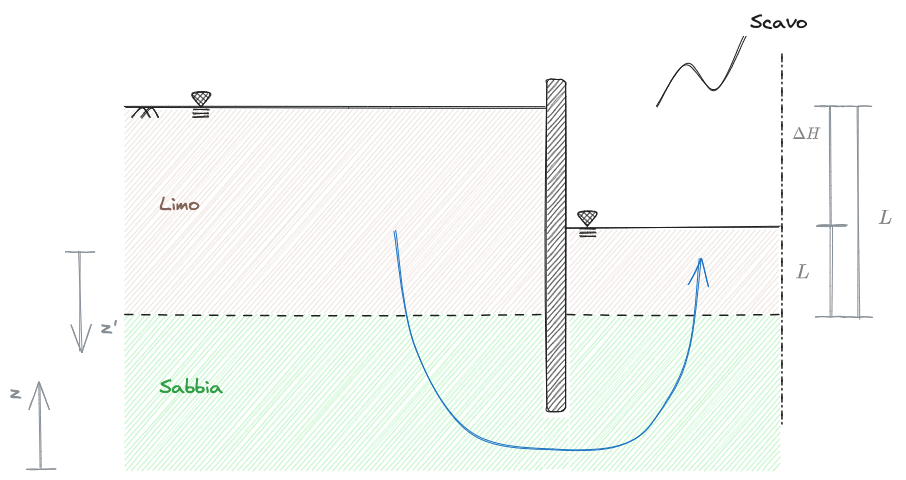
Nei problemi di moti di filtrazione mono-dimensionali, l'#Equazione di Laplace può essere integrata per via analitica.
Questa infatti si scriverà come:

\frac{d^{2} h}{d s^{2}} = 0

che chiaramente integrata fornisce:

h = C_{1} + C_{2} s

Ponendo la profondità dal p.c. pari a $z^{'}$ , l'integrale generale si può scrivere come

h = C_{1} + C_{2} z^{'}

Per ricavare le costanti di integrazione si applicano le condizioni al contorno.
Ricordando il #Carico idraulico $h = z + \frac{u}{γ_{w}}$

{\begin{cases} h (z^{'} = 0) & = L \\ h (z^{'} = L) & = D \end{cases}

Per cui, applicando le c.c. all'integrale generale:

{\begin{cases} h (z^{'} = 0) & = L = C_{2} \\ h (z^{'} = L) & = D = C_{1} L + C_{2} \end{cases}

che in definitiva fornisce i seguenti valori delle costanti:

{\begin{cases} C_{1} = \frac{Δ H}{L} = i \\ C_{2} = L \end{cases}

e quindi la soluzione particolare all'equazione

$h (z^{'}) = i z^{'} + L$

È di interesse anche l'andamento delle pressioni interstiziali $u$ che si può ricavare nel seguente modo:

\begin{aligned} u = (h - z) γ_{w} & = (h - (L - z^{'})) γ_{w} \\ = (i z^{'} + L - L + z^{'}) γ_{w} \\ = (i + 1) γ_{w} z^{'} \end{aligned}

quindi:

andamento $u$

$u (z^{'}) = (i + 1) γ_{w} z^{'}$

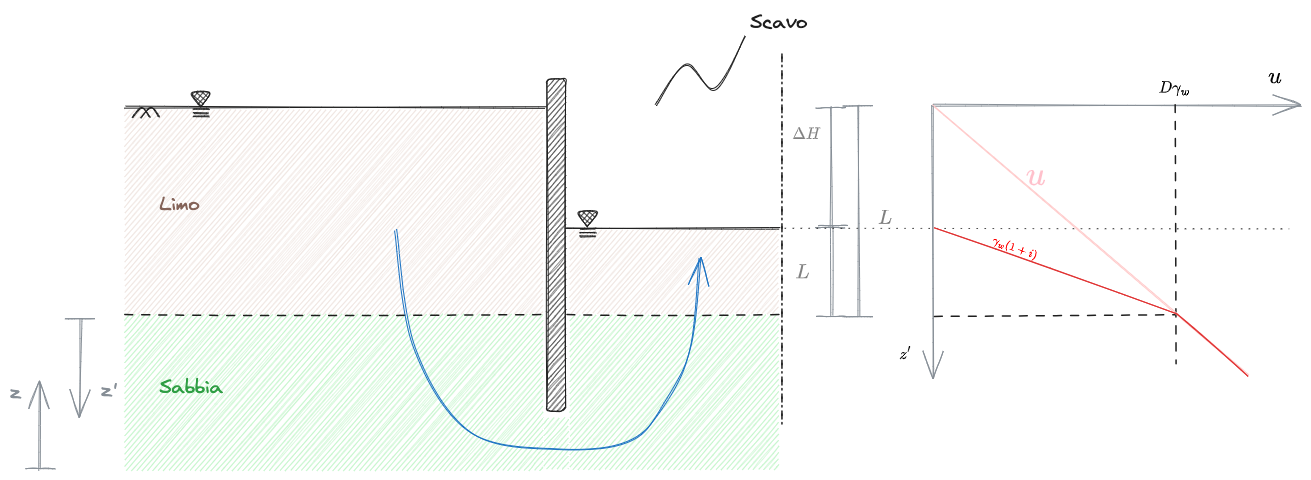
Soluzione bi-dimensionale

Nel caso in cui il moto di filtrazione avvenga sul piano e sia quindi bi-dimensionale diventa molto più complicata l'integrazione dell'#Equazione di Laplace:

\frac{\partial^{2} h}{\partial x^{2}} + \frac{\partial^{2} h}{\partial z^{2}} = 0

essendo questa una equazione differenziale alle derivate parziali.

Il metodo più semplice per risolvere questa equazione è il metodo grafico

Metodo grafico per la soluzione di Laplace in 2D

Il metodo grafico per la #Soluzione bi-dimensionale è basato su alcune proprietà geometriche del sistema che si sta studiando:

Linee equipotenziali: Linee lungo le quali il #Carico idraulico è costante
Linee di massima variazione di $h$ : Linee la cui tangente in ogni punto individua la direzione lungo la quale il #Carico idraulico ha massima variazione (direzione del vettore $\vec{\nabla h}$ )

Nei sistemi in studio in questa sede, le linee di massima variazione di $h$ coincidono con le linee di flusso del moto di filtrazione.

Sia il mezzo a permeabilità isotropa, linee di flusso e equipotenziali si incontrano perpendicolarmente in ogni punto.

Il metodo grafico consiste nel tracciare una serie di linee di flusso e di linee equipotenziali così da costruire il cosiddetto #Reticolo idraulico che deve soddisfare le seguenti condizioni:

condizioni del reticolo idraulico

Le linee di flusso non si incontrano tra loro
Le linee equipotenziali non si incontrano tra loro
Linee equipotenziali e di flusso si incontrano a 90°
Il rapporto tra le dimensioni medie delle maglie è costante (solitamente pari a 1)

In particolare si costruiscono reticoli con rapporto tra dimensioni delle maglie pari a 1: in ogni riquadro del reticolo deve poter essere iscritto un cerchio:

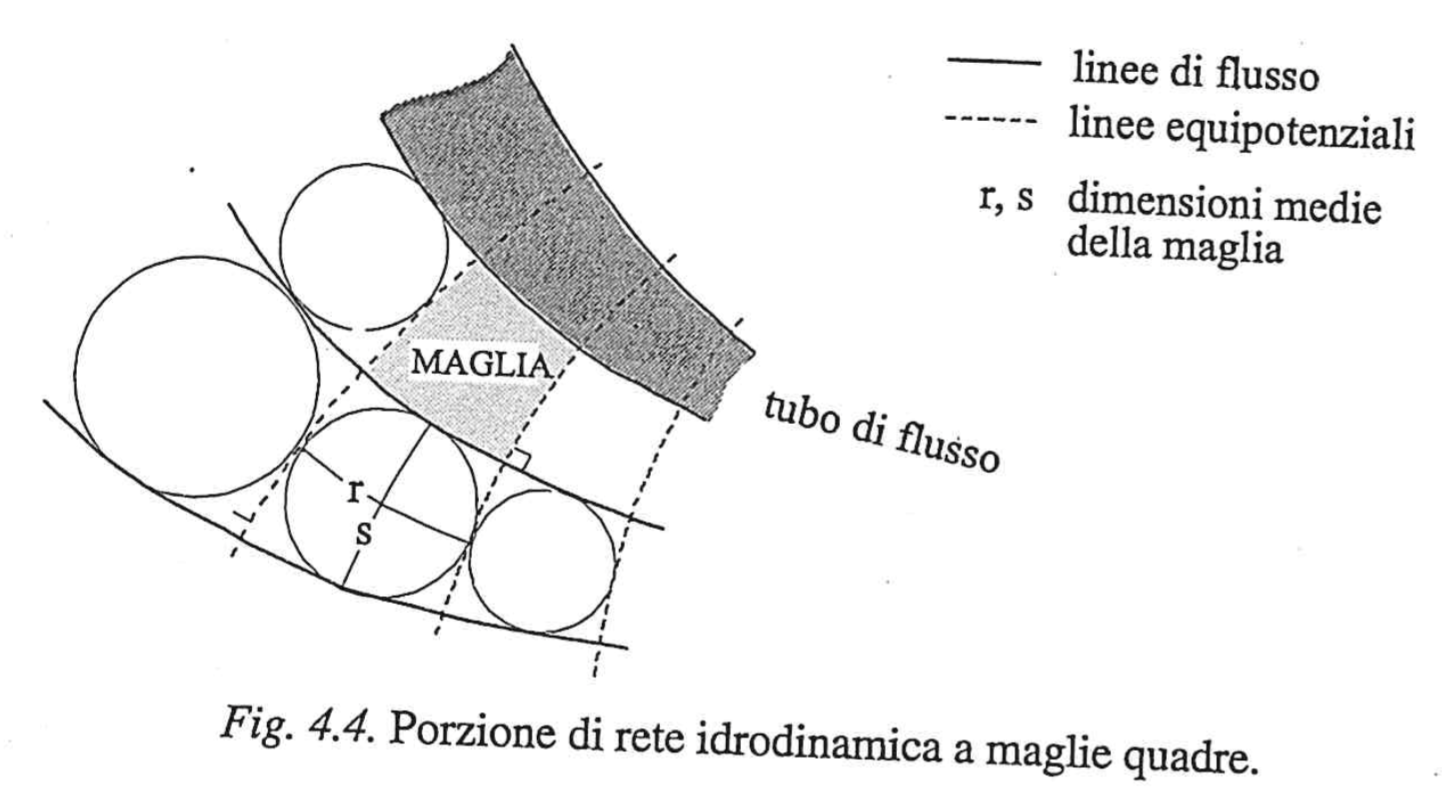
Se le ipotesi sopra sono rispettate, il reticolo gode delle seguenti proprietà:

La perdita di carico complessiva si distribuisce nel sistema in modo che tra due equipotenziali vi sia una perdita di carico pari a $Δ h = \frac{Δ H}{n_{s}}$ dove $n_{s}$ è il numero di salti equipotenziali
La portata, $q$ , è la stessa in tutti gli $n_{t}$ tubi di flusso individuati dalla rete e vale $q = k \frac{Δ H}{n}$ . La portata complessiva, $Q$ , si ottiene moltiplicando la portata elementare per il numero di tubi di flusso: $Q = q n_{t} = k \frac{Δ H}{n_{s}} n_{t}$

The Bizarre Paths of Groundwater Around Structures

esempio

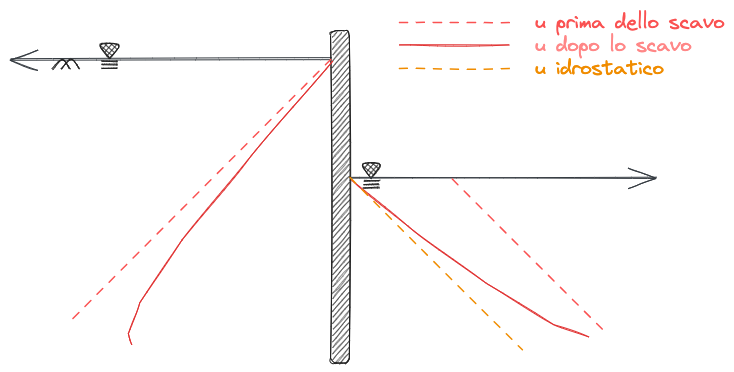
Dato il sistema in figura, si cerca di risolvere e trovare le pressioni interstiziali a destra e a sinistra della paratia.

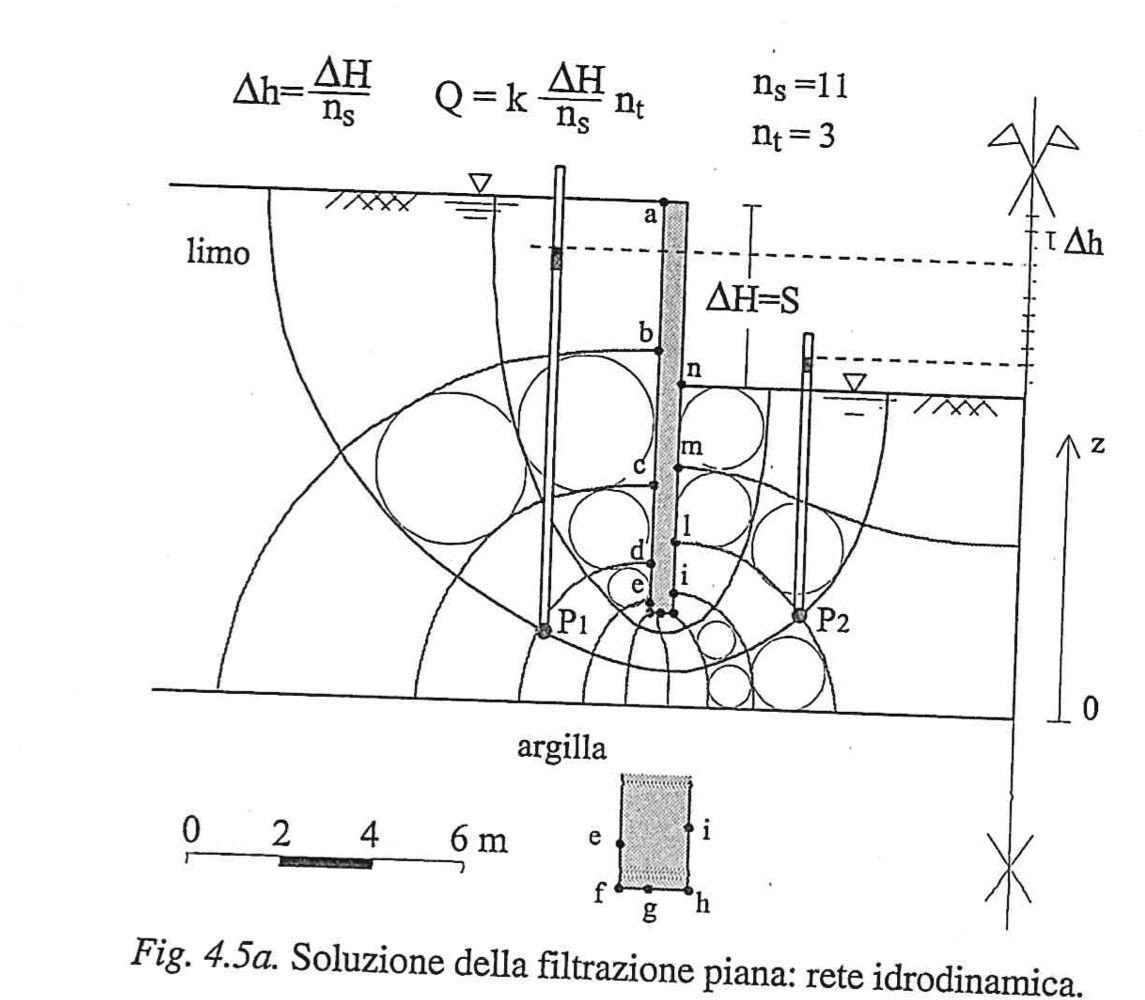
Pasted image 20231218132145.png|550

Si riportano nella tabella sotto i valori calcolati di $h, z, u$ nei vari punti $P$ .

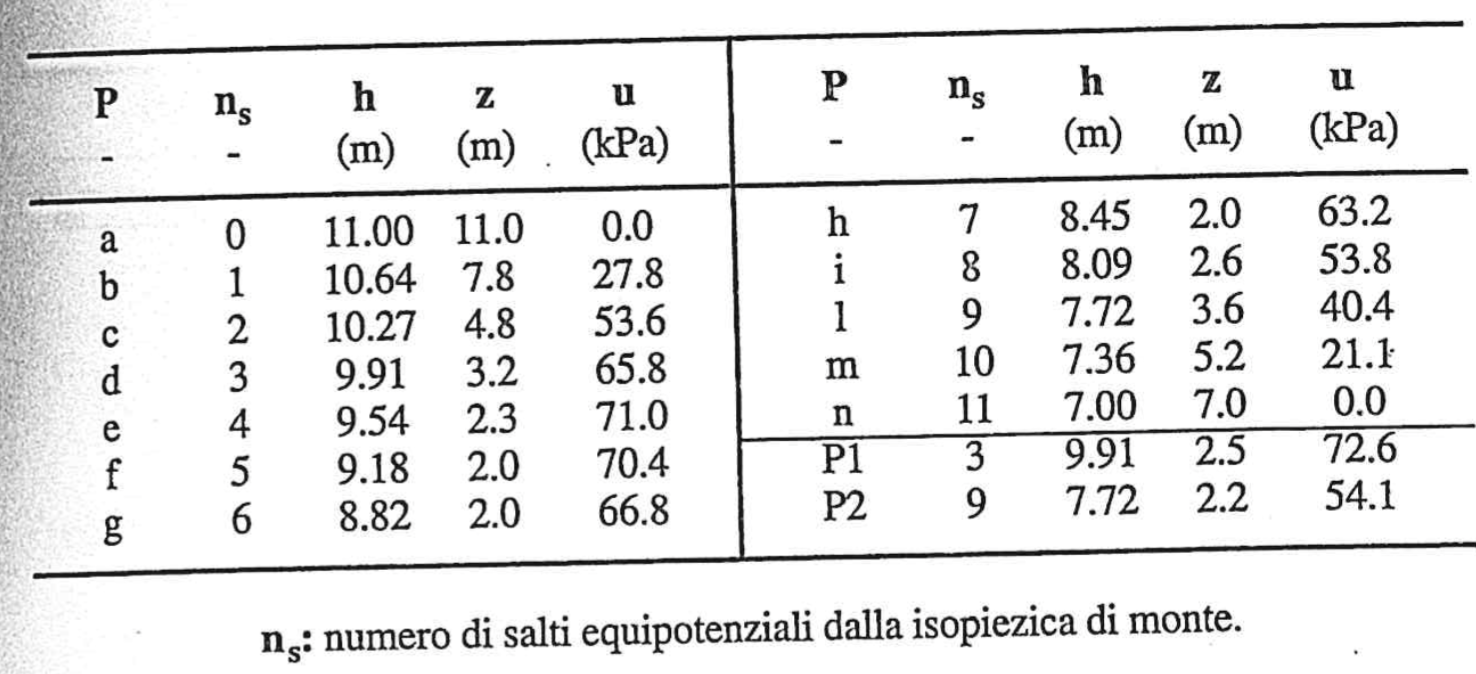
Schermata 2023-12-18 alle 17.41.37.png

Graficandoli questi valori forniscono il seguente grafico

01. Moti di Filtrazione 2023-12-18 17.42.49.excalidraw.png
%%🖋 Edit in Excalidraw%%

L'andamento non è più lineare. In particolare, la u tende ad allontanarsi dalla condizione idrostatica.

Sifonamento e sollevamento fondo scavo

Condizioni particolari del sistema, possono determinare pressioni intersiziali tali da generare fenomeni di instabilità quali #Sifonamento o #Sollevamento fondo scavo.

Sifonamento

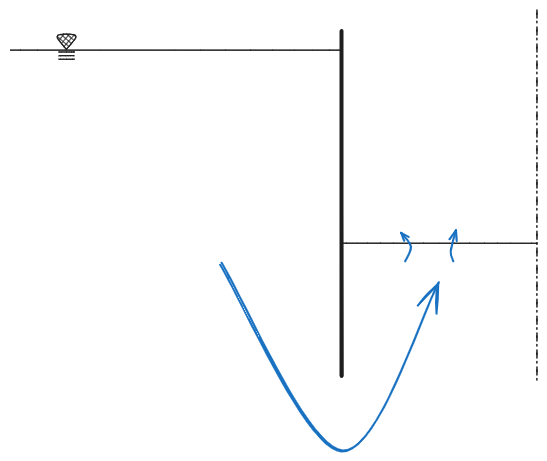
Si immagini la situazione sottostante generica:

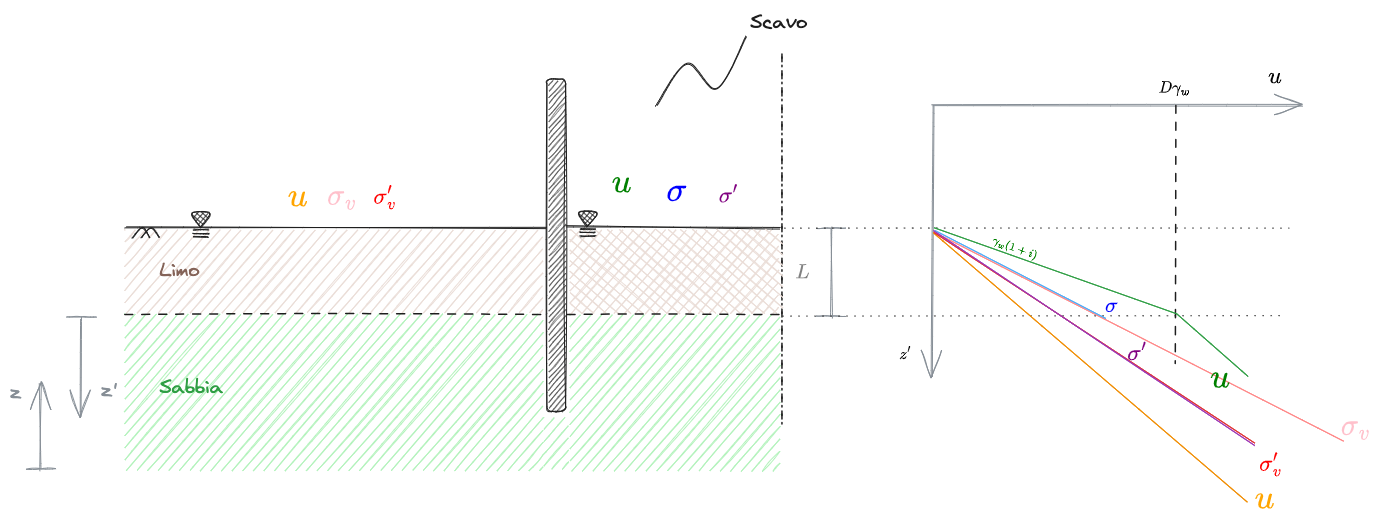
Ora si immagini di innalzare la superficie libera della falda a sinistra della paratia.

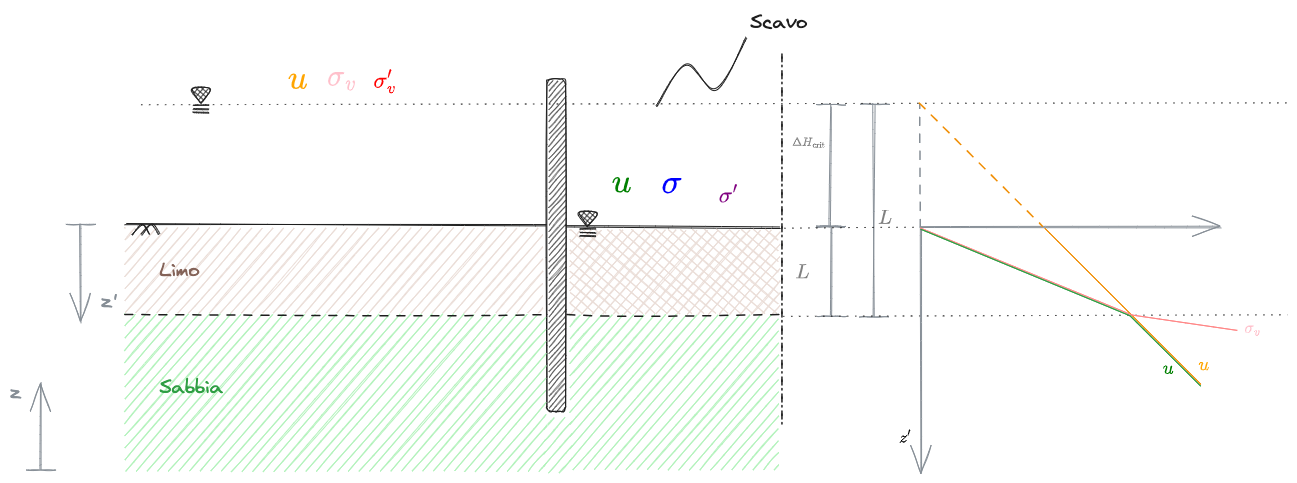
ci sarà un certo innalzamento della falda, $Δ H_{c r i t}$ , per il quale la pressione interstiziale nel #Dominio di filtrazione andrà ad allinearsi con la tensione verticale $σ_{v}$ , facendo si che, in quell'area, le tensioni efficaci siano identicamente pari a zero ( $σ_{v}^{'} \equiv 0$ ).

Il #Carico idraulico vale

{\begin{cases} h = L + Δ H & Fuori dal Dominio di Filtrazione \\ h = L + i z^{'} & Nel Dominio di Filtrazione \end{cases}

Si ha quindi per le pressioni interstiziali $u$ :

u = (1 + i) γ_{w} z^{'}

Ricordando la definizione di tensioni efficaci, le $σ^{'}$ saranno:

\begin{aligned} σ^{'} & = γ z^{'} - u = \\ = γ z^{'} - (1 + i) γ_{w} z^{'} = \\ = (γ - γ_{w} - i γ_{w}) z^{'} = \\ = (γ^{'} - i \cdot γ_{w}) z^{'} \end{aligned}

dove $γ^{'} = γ - γ_{w}$ è il ##peso di volume sommerso.
Si noti che ci sarà un certo valore del #Gradiente Idraulico Critico ( $i_{c r i t}$ ) per cui le tensioni efficaci si annullano in tutto il #Dominio di filtrazione.

gradiente idraulico critico

$i_{c r i t} = \frac{γ^{'}}{γ_{w}}$

L'annullamento delle tensioni efficaci fa si che il terreno sede del fenomeno di filtrazione perda notevolmente di resistenza assumendo la consistenza di un fluido. In queste condizioni, i granuli che compongono il terreno vengono trascinati dal flusso d'acqua andando a generare delle cavità che compromettono notevolmente le proprietà del terreno.

Fattore di sicurezza - sifonamento

Si introduce un fattore per quantificare quanto ci si trovi distanti dalla condizione di #Sifonamento.

fattore di sicurezza

Il fattore di sicurezza è definito come rapporto tra il [[#Gradiente Idraulico]] in condizioni critiche e il gradiente in condizioni di esercizio
$F = \frac{i_{c r i t}}{i_{e s}}$
si avranno i seguenti 3 casi:
${\begin{cases} F > 1 ⟹ Posso sostenere più di quanto arriva \\ F =>= 1 ⟹ Ultima condizione di stabilità \\ F < 1 ⟹ Si verifica il sifonamento \end{cases}$

Rispetto alla situazione illustrata precedentemente, il fattore di sicurezza si può riscrivere ricordando che $i_{c r i t} = \frac{γ^{'}}{γ_{w}}$ e $i_{e s} = \frac{Δ H}{L}$ :

F = \frac{\frac{γ^{'}}{γ_{w}}}{\frac{Δ H}{L}} = \frac{γ^{'} L}{γ_{w} Δ H}

osservazione

Il fattore di sicurezza vade il rapporto tra le seguenti due quantità

$γ^{'} L = \overset{―}{σ_{v}^{'}}$ Tensioni efficaci in condizioni idrostatiche
$γ_{w} Δ H = \overset{―}{Δ u} =$ Eccesso di pressioni interstiziali rispetto alla condizione idrostatica
Secondo queste definizioni, si può scrivere il fattore di sicurezza come:
$F = \frac{\overset{―}{σ_{v}^{'}}}{\overset{―}{Δ u}}$

Il fattore di sicurezza assume solitamente valori compresi tra 2 e 5, a seconda della fragilità dell'opera e dalle condizioni geotecniche di contorno.

Sollevamento di fondo scavo

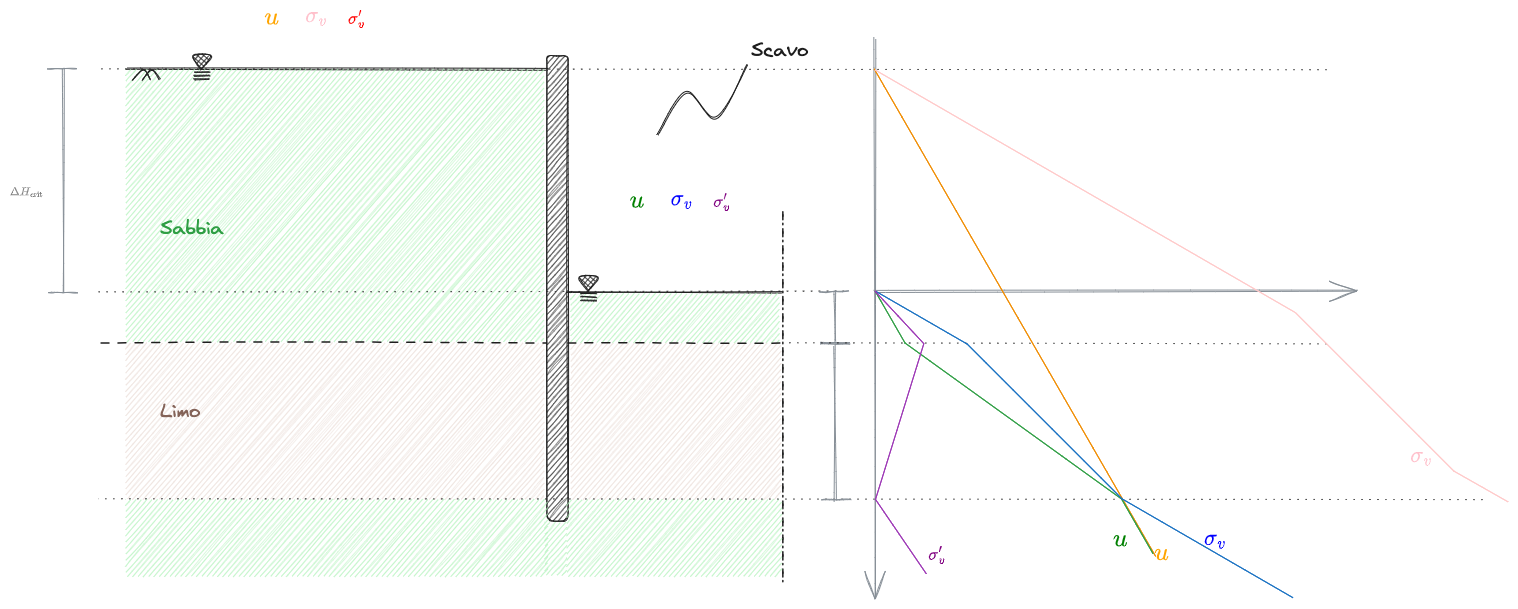
In questo caso si è eseguito uno scavo in un terreno in cui il #Dominio di filtrazione non è il primo strato superficiale, andando a creare un carico idraulico $Δ H$ fino alla particolare condizione in cui, alla base del dominio di filtrazione, è verificata l'uguaglianza $σ_{v} = u$ .
Quando questa condizione è verificata è evidente che si generi alla base del dominio di filtrazione un annullamento delle tensioni efficaci:

σ_{v}^{'} = σ_{v} - u = 0

Questa condizione fa si che il peso del materiale e la spinta idrostatica si eguaglino. Questo è sufficiente a consentire il sollevamento del terreno in superficie nello scavo.

Fattore di sicurezza - Sollevamento

Anche nel caso del #Sollevamento di fondo scavo si procede a definire un fattore di sicurezza.

fattore di sicurezza

$F = \frac{\overset{―}{σ_{v}^{'}}}{\overset{―}{Δ u}}$
dove in questo caso

$\overset{―}{σ_{v}^{'}} = γ_{1}^{'} L_{1} + γ_{2}^{'} L_{2}$
$\overset{―}{Δ u} = γ_{w} Δ H$
e quindi:
$F = \frac{γ_{1}^{'} L_{1} + γ_{2}^{'} L_{2}}{γ_{w} Δ H}$

Anche in questo caso si vuole mantenere
$F ≫ 1$

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ Inserire esercizio di ricavo profondità di scavo critica
❗❗❗❗❗❗❗❗❗❗❗❗❗

Determinazione sperimentale del coefficiente di permeabilità

Il [[#Coefficiente di permeabilità]] può essere determinato per via sperimentale sia in situ, che in laboratorio.
In laboratorio si eseguono le prove su campioni di terreno di dimensioni ridotte (cilindri alti circa $2 \div 2.5 c m$ ).
Le prove in situ avvengono invece scavando un pozzo e modificando il livello dell'acqua per Mungimento o Aspirazione.

In Laboratorio	In Situ
❌ Non sappiamo quanto sia rappresentativo dei dintorni	✅ Fornisce una risposta ben rappresentativa
✅ Conosco perfettamente le condizioni al contorno	❌ Non si conoscono con esattezza le condizioni
✅ È molto economico	❌ Costano molto
✅ Posso fare prove in tutte le direzioni

Di seguito vengono trattate esclusivamente le prove di laboratorio che avvengono generalmente in due modi sfruttando uno strumento detto Permeametro:

#Prove a carico costante
#Prove a carico variabile

Prove a carico costante

Sfrutta un Permeametro a carico costante, ossia un contenitore cilindrico all'interno del quale porre il terreno.

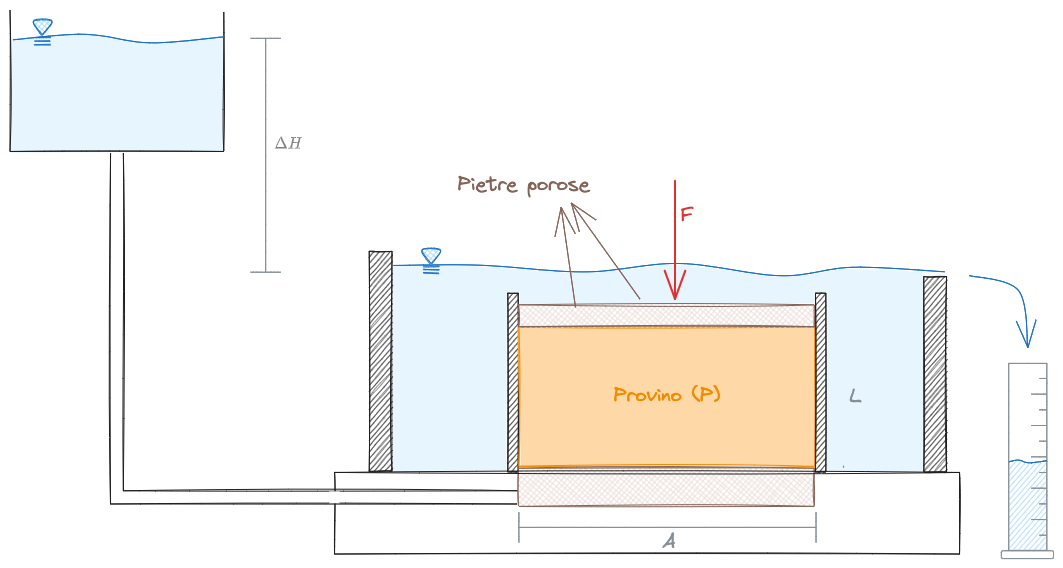
Usando una buretta graduata si misura il volume che transita attraverso il provino.
Si osserva alla relazione

Q = \frac{Δ V}{Δ t}

Questa, dopo una prima fase di transitorio, diventa lineare

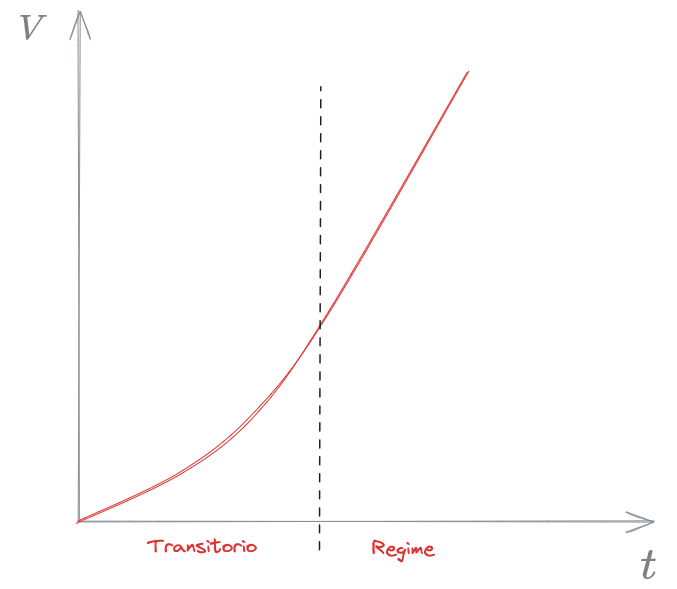
Esplicitando $k$ dalla #Legge di D'Arcy si può così ricavare il coefficiente di permeabilità (essendo nota la geometria del sistema)

$k = \frac{Q}{i A} = \frac{Q L}{Δ H A}$

A causa della scarsa permeabilità di alcuni terreni, in alcuni casi questo metodo è inapplicabile (per le argille).

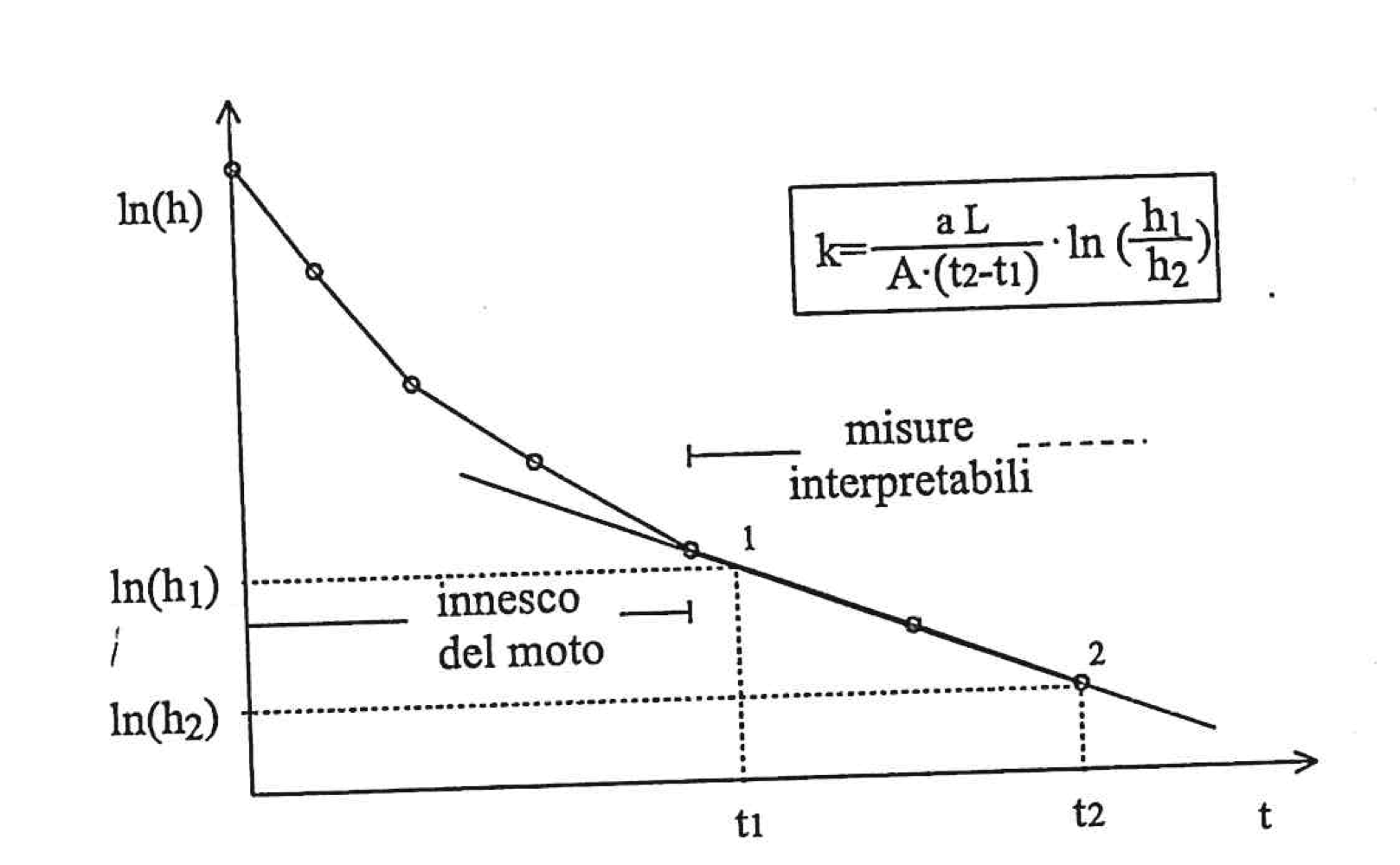
Per evitare fenomeni di #Sifonamento, il provino è posto sotto un carico costante pari ad $F$

Prove a carico variabile

Come visto nelle #Prove a carico costante, per terreni a bassa permeabilità bisogna trovare un metodo più efficace per il calcolo di $k$ .
Nei casi in cui $k$ sia nell'ordine di $10^{- 7} \div 10^{- 9} \frac{m}{s}$ si usa pertanto un Permeametro a carico variabile.
In questo caso non è più presente un serbatoio a monte del sistema.

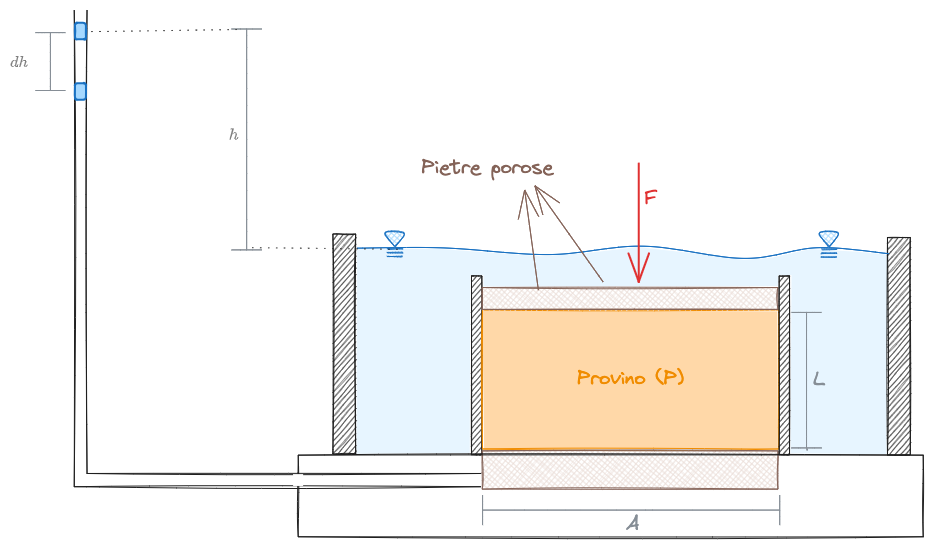
Nel sistema dato ora, in assenza del serbatoio, non si raggiunge mai lo stato stazionario. Si scriverà quindi che il volume d'acqua che attraversa il provino è

d V = Q d t

Sfruttando la #Legge di D'Arcy:

d V = k i A d t = k \frac{h}{L} A d t

Per continuità, questo è lo stesso volume contenuto nel tubo di monte di sezione $a$ nel tratto $d h$ :

d V = k \frac{h}{L} A d t = - a d h

Questa equazione può essere integrata per separazioni di variabili:

\int_{t_{1}}^{t_{2}} k \frac{h}{L} A d t = - \int_{h_{1}}^{h_{2}} a d h

ottenendo per $k$ :

k = \frac{a L}{A (t_{2} - t_{1})} \ln (\frac{h_{1}}{h_{2}})