05. Risoluzione di problemi al finito

Nella progettazione geotecnica occorre risolvere il problema di prevedere gli effetti di una perturbazione applicata al terreno in termini di campo di spostamenti indotto, e di valutazione dei margini di sicurezza rispetto alle condizioni di collasso (coefficienti di sicurezza).

Terreni a grana grossa:
- Rispondono in condizioni drenate
- Effetti contestuali alle perturbazioni
Terreni a grana fine:
- Rispondono in condizioni non drenate
- Effetti NON contestuali alle perturbazioni
  Nei terreni argillosi quindi le analisi di progetto sono più complesse, dovendo prevedere la risposta non drenata.

Equazioni differenziali di governo

Il primo passo alla soluzione del problema al finito consiste nella definizione del modello geotecnico del sottosuolo.
Occorre definire:

Stratigrafie di progetto
Stato tensionale totale ed efficace iniziale
Legame costitutivo da impiegare

La determinazione del comportamento dell'insieme opera-terreno viene ricondotta - schematizzando il terreno come continuo - alla risoluzione di un sistema di equazioni differenziali costituito da:

3 #Equazioni indefinite di equilibrio
3 Equazioni di compatibilità cinematica

Le 6 equazioni forniscono 12 incognite. Chiaramente, a meno di trovare altre 6 equazioni, questo problema non si può risolvere. Le 6 ulteriori equazioni sono fornite dalle equazioni di Legame costitutivo.

Equazioni indefinite di equilibrio

Fanno riferimento a quello che succede all'interno del continuo in ogni punto del continuo.

Considero un punto generico nel continuo. Considero un infinitesimo nel punto e una generica giacitura. Vediamo le forze che agiscono su quell'elemento.

Sono forze che agiscono sulla superficie. In più, se consideriamo la gravità, ci saranno le forze di volume.

equazioni indefinite di equilibrio

Le equazioni indefinite di equilibrio sono le equazioni nelle varie direzioni che devono essere soddisfatte in conseguenza del fatto che l'elemento si trova in equilibrio.

Si dicono indefinite perché devono essere garantite nella totalità dei punti del continuo. Includono anche l'equilibrio alla rotazione.

${\begin{cases} \frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{y x}}{\partial y} + \frac{\partial τ_{z x}}{\partial z} = 0 \\ \frac{\partial τ_{x y}}{\partial x} + \frac{\partial σ_{y}}{\partial y} + \frac{\partial τ_{z y}}{\partial z} = 0 \\ \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial σ_{z}}{\partial z} = γ \end{cases}$
dove

$γ =$ Peso per unità di volume, che tiene conto degli effetti della gravità lungo l'asse verticale.

Le equazioni indefinite di equilibrio non includono l'equilibrio alla rotazione in quanto queste sono già state usate per ridurre il numero delle componenti del #Tensore delle tensioni da 9 a 6

Le funzioni $σ$ e $τ$ sono continue e derivabili nello spazio.

In queste equazioni ci sono tutte le forze con componenti nelle varie direzioni.

$γ$ è il peso per unità di volume. Nella direzione $z$ infatti conta anche la gravità.

Il peso va considerato perché le terre hanno un comportamento estremamente non lineare nonché plastico.

Equazioni di compatibilità cinematica

equazioni di compatibilità cinematica

Le equazioni di compatibilità cinematica, dette anche equazioni di congruenza, garantiscano l'assenza di fenomeni di:

lacerazioni
compenetrazioni di materia

${\begin{cases} \frac{\partial^{2} ε_{x}}{\partial y^{2}} + \frac{\partial^{2} ε_{y}}{\partial x^{2}} - \frac{\partial^{2} γ_{x y}}{\partial x \partial y} = 0 \\ \frac{\partial^{2} ε_{x}}{\partial z^{2}} + \frac{\partial^{2} ε_{z}}{\partial x^{2}} - \frac{\partial^{2} γ_{x z}}{\partial x \partial z} = 0 \\ \frac{\partial^{2} ε_{y}}{\partial z^{2}} + \frac{\partial^{2} ε_{z}}{\partial y^{2}} - \frac{\partial^{2} γ_{y z}}{\partial y \partial z} = 0 \end{cases}$

Garantiscono che quando applico dei carichi ad un continuo, questo si deformi.

Equazioni di legame costitutivo

Le equazioni di legame costitutivo sono quelle date sulla base del Legame costitutivo scelto.
Permettono di scrivere gli incrementi di deformazione in termini di incrementi di sforzo o viceversa.

\underset{―}{δ ε} = \underset{―}{\underset{―}{C}} \underset{―}{δ σ}

Risoluzione delle equazioni di governo

Facendo riferimento a Legami costitutivi elasto-plastici (incrudenti e non), il problema deve essere risolto mediante l'utilizzo di metodi approssimati, quali

Elementi finiti
Differenze finite
...

Approcci semplificati e soluzioni in forma chiusa

Nella maggior parte delle applicazioni si sceglie di costruire dei modelli semplificati così da evitare di essere costretti ad utilizzare i calcolatori.
Questo approccio, seppur semplice non può che essere meno accurato di un metodo numerico.

Alla base vi è una differenziazione tra

Problemi di comportamento in esercizio
Problema di Valutazione dei margini di sicurezza nei riguardi della formazione di meccanismi di collasso

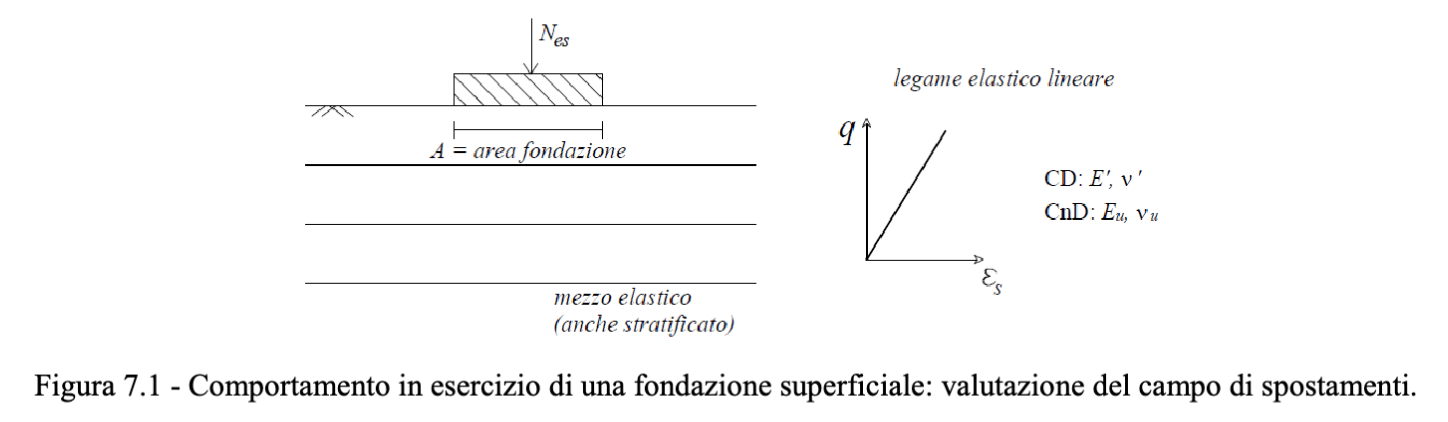
Problemi di comportamento in esercizio
Si utilizza il legame costitutivo elastico lineare. In questo modo, il sistema di #Equazioni differenziali di governo presenta soluzione in forma chiusa, consentendo di valutare gli spostamenti indotti da una perturbazione esterna.
Tipico esempio è la valutazione dei cedimenti di una fondazione superficiale.

Valutazione dei margini di sicurezza nei riguardi della rottura (meccanismi di collasso)
In questo caso si fa ricorso a modelli rigidi plastici perfetti: si trascura la parte di comportamento elastico e l'eventuale incrudimento.
Le verifiche di stabilità vengono condotte per mezzo dei #Teoremi di estremo superiore e inferiore che consentono di valutare in modo agevole i carichi di collasso e, dunque, i margini di sicurezza della perturbazione applicata rispetto a quella limite.

Si tenga presente che il carico in esercizio è:

q_{e s} = \frac{N_{e s}}{A}

Mentre il valore di carico limite (rottura) è:

q_{l i m} = c N_{c} + q N_{q} + \frac{1}{2} γ_{b} B N_{γ}

dove:

$γ_{b} =$ Peso di volume sommerso del terreno
$B =$ Larghezza della fondazione
$N_{c}, N_{q}, N_{γ} =$ fattori di capacità portanti dipendenti dall'angolo di attrito del terreno

Si può definire il #Coefficiente di Sicurezza:

F = \frac{q_{l i m}}{q_{e s}}

Le relazioni appena viste vanno intese:

In termini di tensioni totali $⟺$ condizioni non drenate
In termini di tensioni efficaci $⟺$ condizioni drenate

In definitiva, il comportamento reale elasto-plastico incrudente viene diviso in 2, studiando separatamente:

Comportamento in esercizio (elastico)
Verifiche di stabilità (plastico)

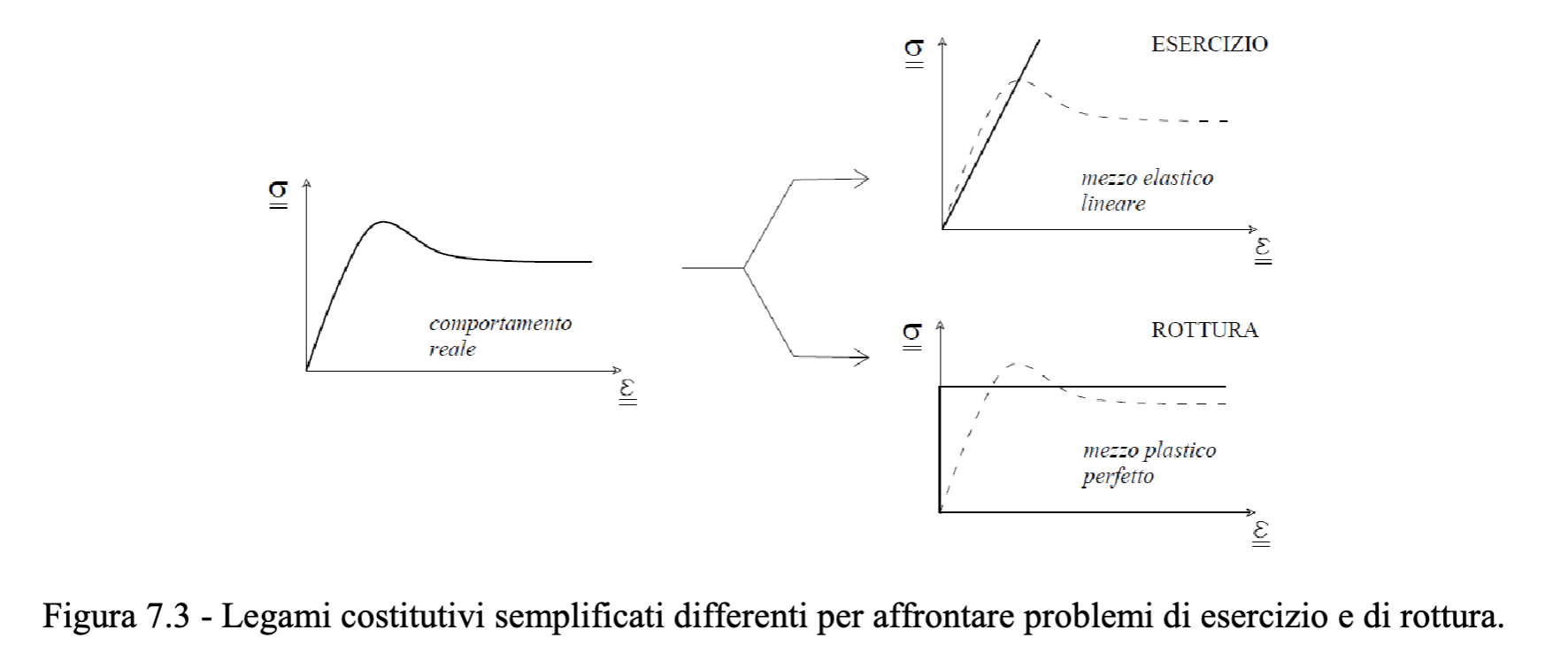
Soluzioni approssimate ottenute mediante analisi numeriche

Bisogna differenziare tra le soluzioni ottenute in riferimento a condizioni drenate o non drenate.

#Soluzione in CND
#Soluzione in CD

Soluzioni in CND e CD

Soluzione in CND

Il problema può essere affrontato sia in termini di tensioni totali che di tensioni efficaci.

Tensioni totali:
Si rinuncia alla divisione scheletro solido - acqua interstiziale e si considera un unico mezzo monofase caratterizzato da parametri di deformabilità e resistenza espressi in termini di tensioni totali.
SI avranno:

Esercizio - elastico lineare - Modulo di Young non drenato: $E_{u}$
Resistenza - plastico perfetto - Coesione non drenata: $c_{u}$

Tensioni Efficaci:
Impongo l'ulteriore condizione $δ ε_{v} = 0$ : drenaggio impedito.
Il modello studia quindi l'interazione acqua-scheletro solido ed è in grado di valutare le pressioni interstiziali indotte al termine dell'applicazione della perturbazione esterna e il successivo processo di consolidazione.

Immaginando di adottare per lo scheletro solido un Legame costitutivo elasto-plastico perfetto con criterio di resistenza di Mohr-Coulomb, i parametri di deformabilità e resistenza sono:

Deformabilità: $E^{'}, ν^{'}$
Resistenza: $c^{'}, φ^{'}$

Soluzione in CD

Se si studia il sistema in condizioni drenate (argilla in lungo termine, sabbie sotto carichi statici), occorre fare in modo che non si generino sovrappressioni interstiziali.

Determinazione dei margini di sicurezza

Il Margine di sicurezza F può essere determinato seguendo due procedure diverse:

Si incrementa gradualmente l'intensità della perturbazione esterna sino a quando non si genera un meccanismo di collasso. Si ottiene quindi: $F = \frac{q_{l i m}}{q_{e s}}$
La perturbazione esterna è mantenuta cotante mentre si variano i parametri di resistenza del terreno. Si ottiene il fattore di sicurezza come: rapporto tra resistenza caratteristica del terreno e resistenza per la quale si raggiunge condizioni di incipiente collasso

Teoremi di estremo

Nell'affrontare i problemi di stabilità - e quindi determinazione dei margini di sicurezza, condizioni di equilibrio limite - si fa ricorso all'utilizzo del modello rigido plastico perfetto con legge di flusso associato e non.
In questo modo, pur rinunciando a seguire il comportamento complesso opera-terreno, si ottengono soluzioni sufficientemente approssimate delle condizioni di collasso, usando strumenti di calcolo elementari (calcolatrici).

Si hanno quindi 2 teoremi di estremo

#Teorema di Estremo Superiore - TES
#Teorema di Estremo Inferiore - TEI

I teoremi di estremo permettono di definire un range all'interno del quale si trova il carico di collasso effettivo, $q_{l i m, r e a l e}$ . Più ampio è questo range, meno sappiamo della soluzione esatta.
Nel caso ideale in cui $p_{l i m, i} = p_{l i m, r e a l e} = p_{l i m, u}$ si avrebbe proprio la soluzione esatta.
Nel caso di range molto ampio, occorrerà cercare nuovi valori di upper e lower bound.

Quando si ha un range soddisfacentemente piccolo, si può assumere il valore inferiore come valore limite (in nome della sicurezza), e usare quello per le applicazioni ingegneristiche.

Teorema di Estremo Superiore - TES

tes - teorema di estremo superiore (upper bound)

I valori dei carichi esterni (perturbazioni) ottenuti eguagliando il lavoro delle forze esterne, $δ L_{e}$ , al lavoro dissipato per attrito interno, $δ L_{i}$ , in un meccanismo di rottura cinematicamente compatibile, $p_{l i m, u}$ , approssimano per eccesso i reali carichi di collasso, $p_{l i m}$ , o al limite, coincidono con essi.

Applicare il TES significa soddisfare le #Equazioni di compatibilità cinematica (eq. di congruenza) ma NON soddisfare le #Equazioni indefinite di equilibrio. Qualora si applicasse il carico di estremo superiore, per un tempo sufficientemente lungo, si raggiungerebbero di certo le condizioni di collasso.

Teorema di Estremo Inferiore - TEI

tei - teorema di estremo inferiore (lower bound)

I valori dei carichi esterni in equilibrio con una distribuzione di tensioni che soddisfa in ogni punto del mezzo le #Equazioni indefinite di equilibrio e che non viola in alcun punto il criterio di plasticizzazione (rottura), $p_{l i m, i}$ , approssimano per difetto i reali carichi di collasso o, al limite, coincidono con essi.

Applicando i carichi così ottenuti al continuo, il sistema risulterebbe stabile o, al più, in condizioni di equilibrio limite.

Applicazione dei teoremi di estremo

Si studia ora l'applicazione dei #Teoremi di estremo. Per farlo, si fanno alcune ipotesi sul mezzo che si prende in esame:

ipotesi per l'applicazione di tes e tei

Mezzo continuo ideale (monofase)
Mezzo rigido plastico perfetto (RPP)
Legge di flusso associata

Si studia la situazione mostrata in figura:
Si vuole cercare per quale valore limite di un carico $q$ , (al limite $q_{l i m}$ ), si raggiungono le condizioni di plasticizzazione.

Il carico $q$ è applicato per un estensione $b$ .
Al di fuori della striscia di carico agisce un sovraccarico $q_{0}$

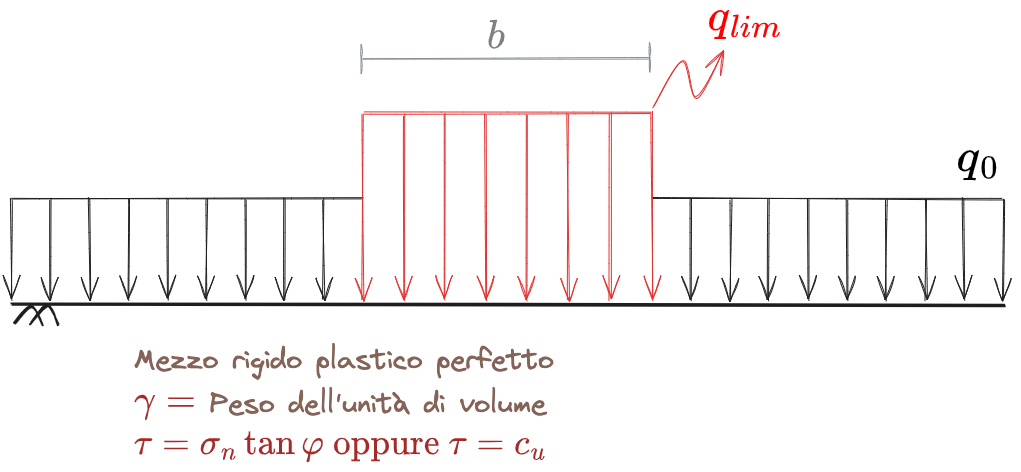
Per applicare i #Teoremi di estremo, in particolare per il TES occorre individuare dei meccanismi di rottura che siano cinematicamente compatibili: non ci devono essere

Compenetrazioni di materia
Lacerazioni di materia
In breve, devono essere rispettate le #Equazioni di compatibilità cinematica.

In genere si manifestano dei meccanismi di rottura individuati da cunei, i quali scorrono in modo relativo tra loro. La rottura si concentra pertanto in una fascia, di spessore $d S$ . Questa è quindi la fascia dove si concentrano le deformazioni plastiche.

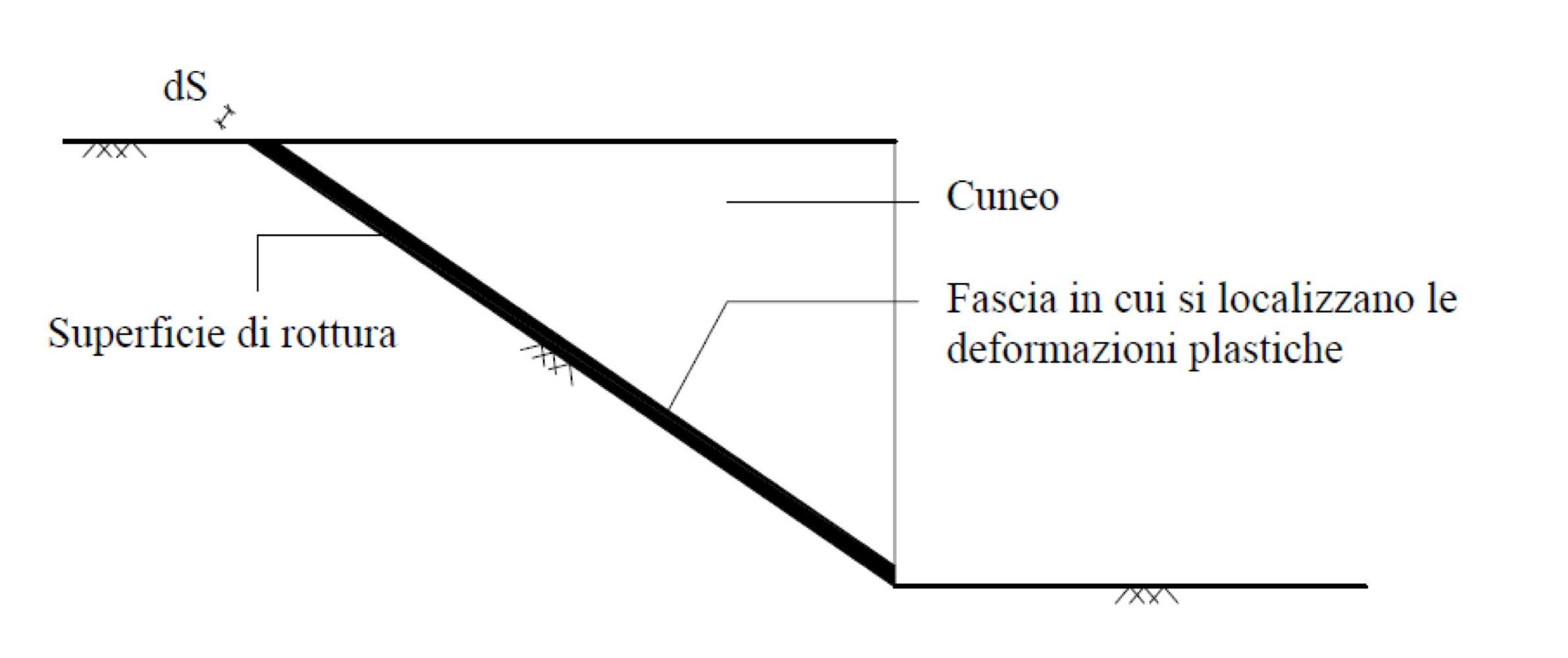
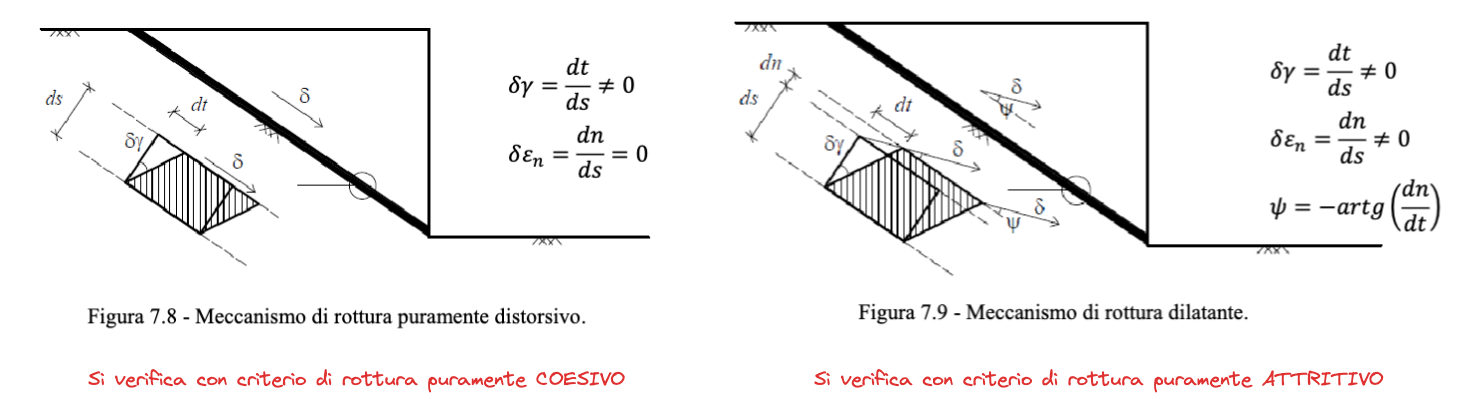
Avendo fatto l'ipotesi di legge di flusso associata, il meccanismo di rottura dovrà avvenire in modo da rispettare tale ipotesi:

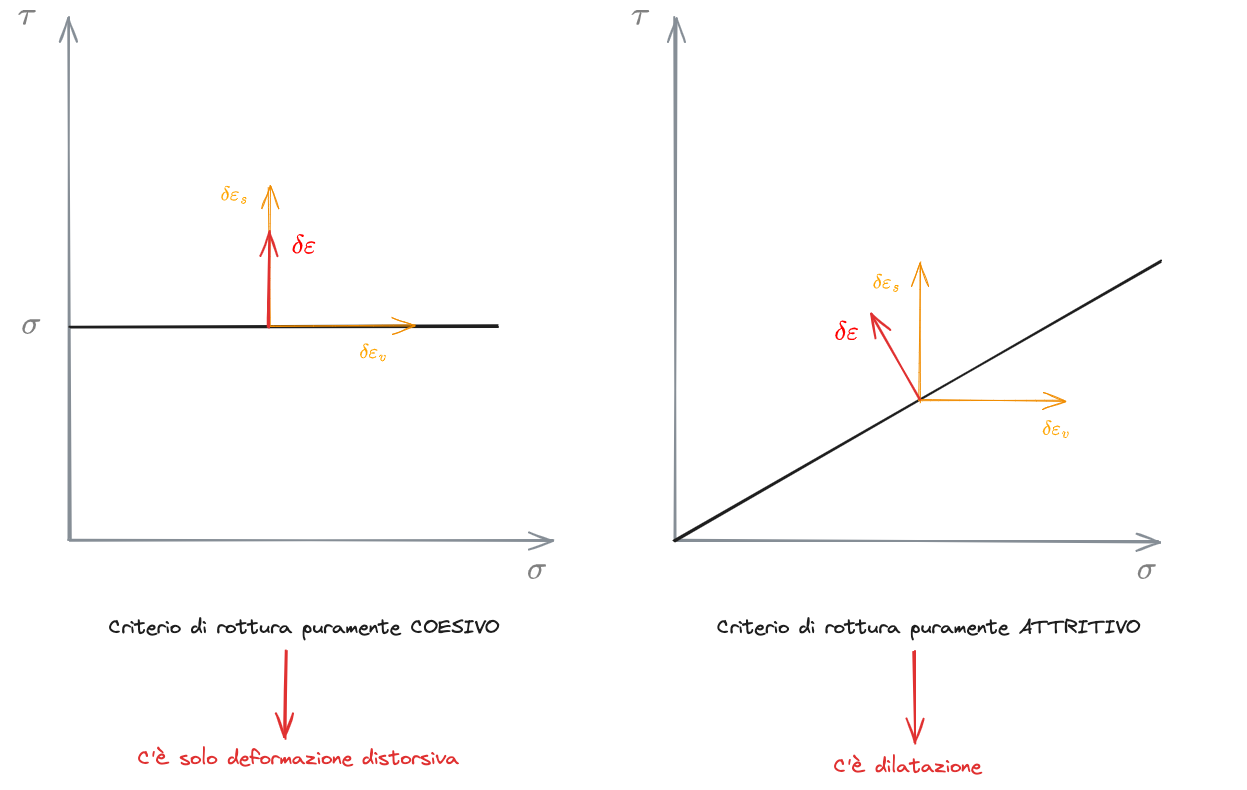
Per la legge di flusso associata, vediamo che ci sono due possibilità:

Deformazione esclusivamente distorsiva - associata a un criterio di rottura puramente coesivo
Deformazione comprensiva di dilatanza - associata a un criterio di rottura puramente attritivo

Applicazione dei Teoremi di Estremo - Mezzo Puramente COESIVO

TES - Mezzo puramente COESIVO

Si ricorda il TES:

Teorema di Estremo Superiore - TES

tes - teorema di estremo superiore (upper bound)

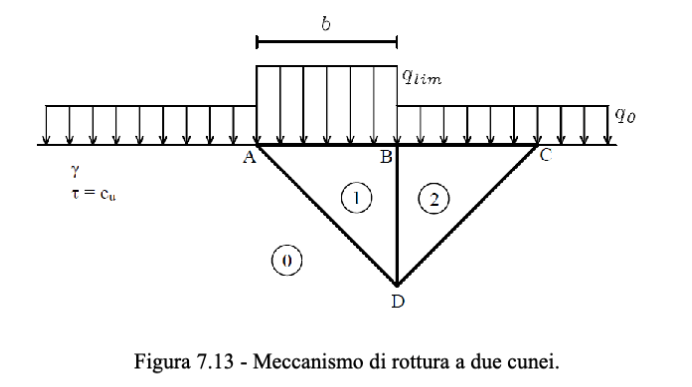
Al fine di applicare i #Teoremi di estremo è necessario supporre dei meccanismi di rottura. Si sceglie in questo caso un meccanismo a 2 cunei, come in figura.

Come visto, in caso di mezzo puramente coesivo, nel rispetto della legge di flusso associato, l'unico meccanismo di rottura ipotizzabile è quello puramente distorsivo, senza alcuna dilatanza.
Gli unici movimenti da prendere in considerazione sono quelli tra il cuneo 1 e il cuneo 2.
Un meccanismo di rottura compatibile con quanto detto, è quello mostrato nella figura sottostante:

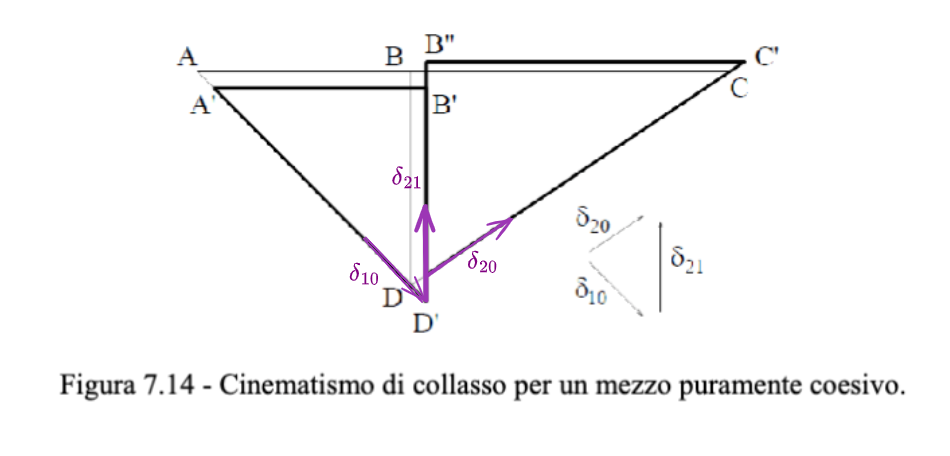
Si individuano i seguenti spostamenti relativi:

$δ_{10}$ - Spostamento del cuneo 1 rispetto al terreno indisturbato (0)
$δ_{20}$ - Spostamento del cuneo 2 rispetto al terreno indisturbato (0)
$δ_{21}$ - Spostamento del cuneo 2 rispetto al cuneo 1

Al fine di evitare compenetrazioni, tutti gli spostamenti relativi $δ$ , devono verificarsi parallelamente alle superfici individuate come superfici di rottura.
Inoltre lo spostamento assoluto del cuneo 2, deve essere risultante della somma vettoriale di $δ_{10}$ e $δ_{21}$ :

δ_{20} = δ_{10} + δ_{21}

Fatte queste considerazioni, si può procedere ad applicare il TES.
L'obiettivo è eguagliare il lavoro compiuto dalle forze esterne a quello compiuto dalle forze interne:

δ L_{e} = δ L_{i}

Le forze esterne che compiono lavoro sono:

La risultante del carico a rottura: $Q = q_{l i m} b$
La risultante del sovraccarico esterno nel tratto $B C$ : $Q_{e} = q_{0} B C$
Il peso dei cunei: $W_{1}, W_{2}$

Le forze interne che compiono lavoro sono:

L'attrito (tensione tangenziale) tra i due cunei: $τ$
L'attrito tra ogni cuneo e il terreno esterno: $τ$

Si calcolano i lavori delle forze esterne e delle forze interne:

\begin{aligned} δ L_{e} & = q_{l i m} b \cdot δ_{10 v} + W_{1} \cdot δ_{10 v} + + W_{2} \cdot δ_{20 v} + q_{0} B C \cdot δ_{20 v} \\ δ L_{i} & = τ A D \cdot δ_{10} + τ C D \cdot δ_{20} + τ B D \cdot δ_{21} \end{aligned}

dove si sono considerate solo le componenti degli spostamenti $δ$ lungo le quali i carichi o i pesi compiono effettivamente lavoro (le componenti verticali).

A questo punto si eguagliano i due lavori:

q_{l i m} b \cdot δ_{10 v} + W_{1} \cdot δ_{10 v} + + W_{2} \cdot δ_{20 v} + q_{0} B C \cdot δ_{20 v} = τ A D \cdot δ_{10} + τ C D \cdot δ_{20} + τ B D \cdot δ_{21}

Essendo la geometria nota, riscrivendo tutti i $δ$ in funzione di un unico spostamento relativo o assoluto, ad esempio, $δ_{10}$ , questo si semplificherà. A questo punto si può procedere a risolvere per il carico limite, $q_{l i m}$ .
Ipotizzando $A B = B C$ e $A \hat{D} C = 90 °$ , si otterrebbe un valore di carico limite pari a:

q_{l i m, u} = q_{0} + 6 c

TEI - Mezzo puramente COESIVO

Si ricorda il TEI:

Teorema di Estremo Inferiore - TEI

tei - teorema di estremo inferiore (lower bound)

I valori dei carichi esterni in equilibrio con una distribuzione di tensioni che soddisfa in ogni punto del mezzo le [[#Equazioni indefinite di equilibrio]] e che non viola in alcun punto il criterio di plasticizzazione (rottura), $p_{l i m, i}$ , approssimano per difetto i reali carichi di collasso o, al limite, coincidono con essi.

Applicando i carichi così ottenuti al continuo, il sistema risulterebbe stabile o, al più, in condizioni di equilibrio limite.

Si ricorda la geometria del problema. Si sceglie la più semplice distribuzione di tensione che soddisfi le [[#Equazioni indefinite di equilibrio]]. Questa corrisponde a quella incontrata in corrispondenza di una discontinuità lungo i bordi di carico (la superficie tra $q_{l i m}$ e $q_{0}$ ).

Essendo il problema simmetrico, si può guardare a solo una delle due porzioni del sistema in esame.

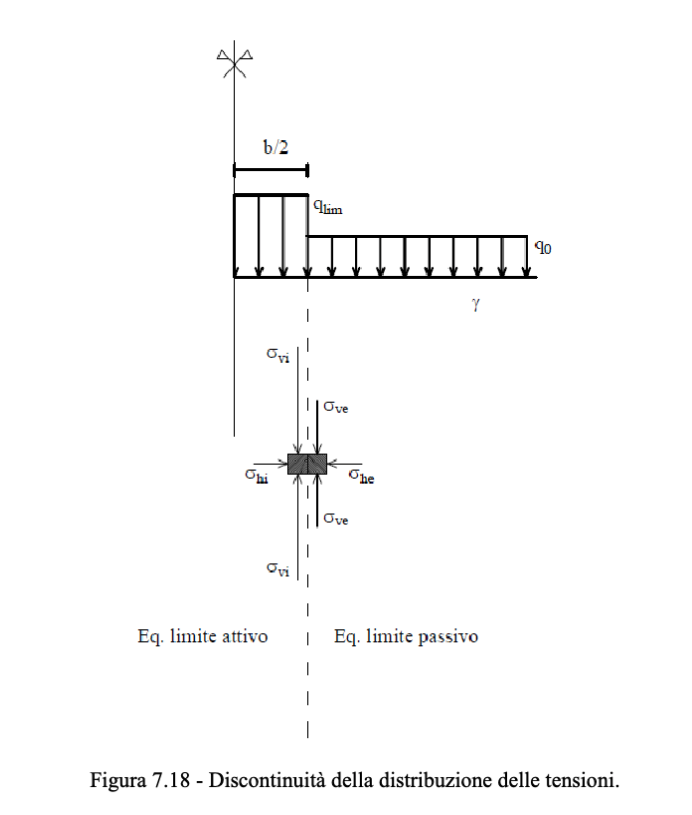
Tensioni verticali interne:
All'esterno del corpo di carico la tensione verticale è:

σ_{z e} = q_{0} + γ z

L'equilibrio alle tensioni orizzontali è soddisfatto per qualsiasi valore di $σ_{h e}$ .

σ_{h e} = σ_{h i} sempre

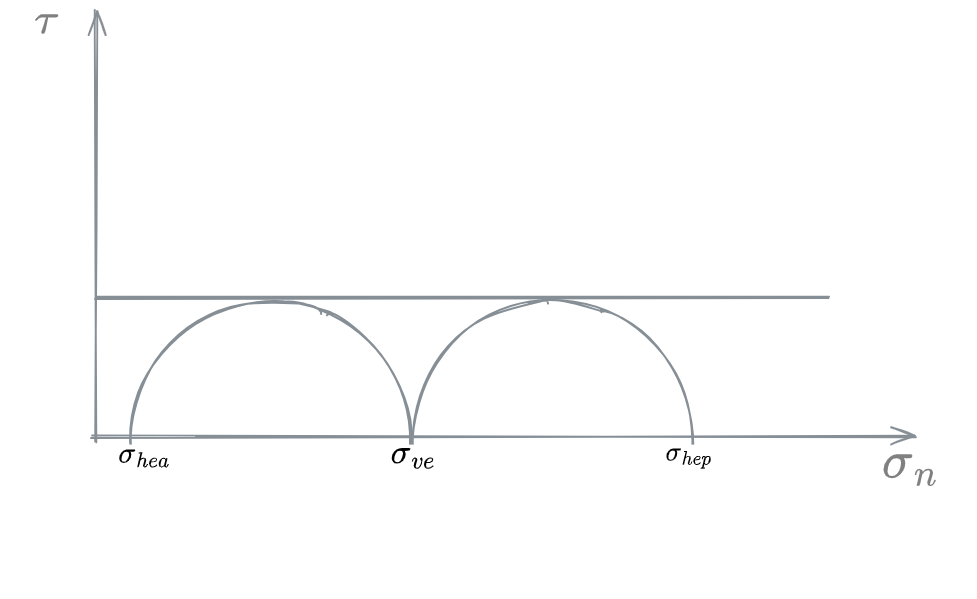
In criterio di resistenza puramente coesivo, la $σ_{h e}$ non può che oscillare tra i valori di tensioni orizzontali limite in condizioni attive e passive.

Tensioni orizzontali esterne:
Pertanto sarà:

\begin{aligned} σ_{h e a} & \leq σ_{h e} \leq σ_{h e p} \\ σ_{v e} - 2 c & \leq σ_{h e} \leq σ_{v e} + 2 c \end{aligned}

Ipotizziamo le condizioni passive: $σ_{h e} > σ_{h i}$
Abbiamo detto:

σ_{v e} = q_{0} + γ z σ_{h e} = σ_{h e p} = σ_{v e} + 2 c

quindi:

σ_{h e} = q_{0} + γ z + 2 c

Tensioni orizzontali interne:
Abbiamo già detto $σ_{h i} = σ_{h e}$ per il rispetto delle equazioni di equilibrio. Pertanto:

σ_{h i} = q_{0} + γ z + 2 c

Tensioni verticali interne:
Dovendo rispettare le condizioni di rottura coesive, il valore, fissato le $σ_{h i}$ è obbligato.
Si avrà infatti che, dovendo comunque essere $σ_{v i} > σ_{v e}$ :

σ_{v i} = σ_{h i} + 2 c

quindi, ricordando $σ_{h i} = q_{0} + γ z + 2 c$ :

σ_{v i} = q_{0} + γ z + 4 c

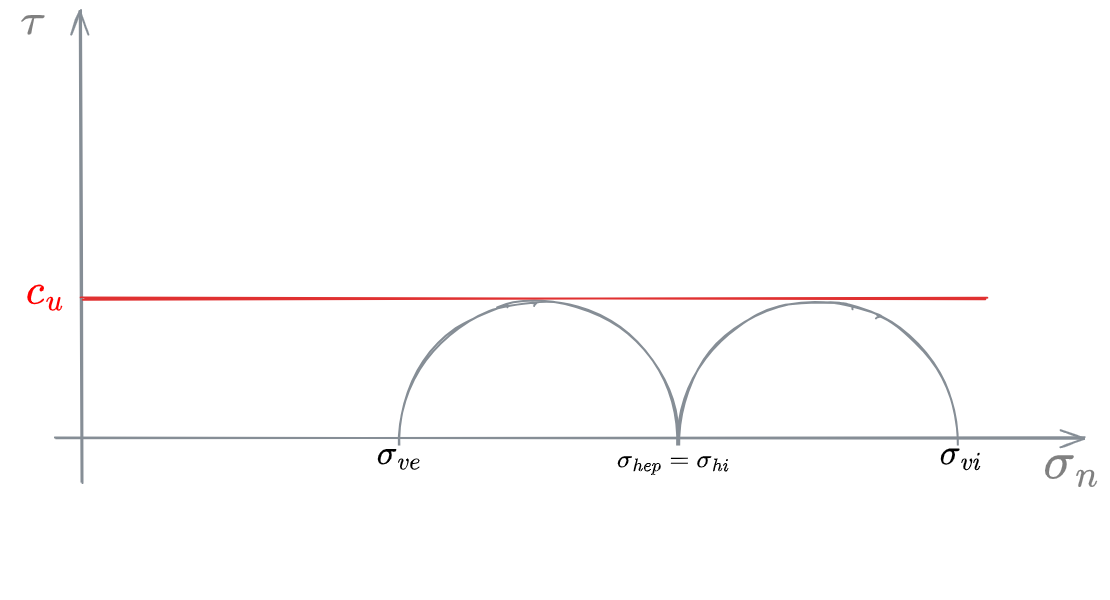
Si ha pertanto che, il valore di $q_{l i m, l}$ è quello di $σ_{v i}$ che si ha per quota $z = 0$ :

q_{l i m, l} = q_{0} + 4 c

che ricordando il valore ottenuto nell'applicazione del #TEI - Mezzo puramente COESIVO ( $q_{l i m, u} = q_{0} + 6 c$ ) risulta effettivamente minore.

Applicazione dei Teoremi di Estremo - Mezzo Puramente ATTRITIVO

TES - Mezzo puramente ATTRITIVO

TEI - Mezzo puramente ATTRITIVO

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗