03. Legame costitutivo - studio

legame costitutivo

Un modello costitutivo è una legge matematica che mette in relazione le variazioni di stato di sforzo con le variazioni di stato di deformazione.
$\underset{―}{δ ε} = \underset{―}{\underset{―}{C}} \cdot \underset{―}{δ σ}$
dove:

$δ ε =$ Incremento dello stato di deformazione
$δ σ =$ Incremento dello stato di sforzo
$C =$ Matrice di cedevolezza o matrice costitutiva

Si tratta di un'applicazione lineare che, applicato al [[#tensore delle tensioni]], fornisce il [[#Tensore delle deformazioni]].

Ad esempio, la Legge di Hooke.

ε = C σ

Da un punto di vista formale, le componenti del tensore di deformazione possono essere raccolte in un vettore di 6 componenti (vista la simmetria). Lo stesso posso fare con il tensore delle tensioni.

\begin{aligned} ε = [\begin{array}{c} ε_{x} \\ ε_{y} \\ ε_{z} \\ γ_{x y} \\ γ_{x z} \\ γ_{y z} \end{array}] & σ = [\begin{array}{c} σ_{x} \\ σ_{y} \\ σ_{z} \\ τ_{x y} \\ τ_{x z} \\ τ_{y z} \end{array}] \end{aligned}

Si ha che li legame costituivo sarà:

C = [\begin{matrix} C_{11} & \dots & C_{16} \\ \dots \\ \dots \\ \dots \\ \dots \\ \dots & C_{66} \end{matrix}]

Per le terre si ha che il legame vale per un piccolo incremento di tensione / deformazione:

[\begin{matrix} δ ε_{x} \\ δ ε_{y} \\ δ ε_{z} \\ δ γ_{x y} \\ δ γ_{x z} \\ δ γ_{y z} \end{matrix}] = [\begin{matrix} C_{11} & \dots & C_{16} \\ \dots \\ \dots \\ \dots \\ \dots \\ \dots & C_{66} \end{matrix}] \cdot [\begin{matrix} δ σ_{x} \\ δ σ_{y} \\ δ σ_{z} \\ δ τ_{x y} \\ δ τ_{x z} \\ δ τ_{y z} \end{matrix}]

I coefficienti cambiano per ogni incremento infinitesimo di $ε$ e $σ$ .

attenzione!

Per semplicità, da ora in poi si lavora in assial-simmetria

In presenza di assial-simmetria, si può descrivere lo stato di tensione mediante due #Invarianti di tensione:

Invarianti di tensione

Gli invarianti di tensione sono

La #Pressione media
Lo #Sforzo deviatorico

Pressione media

pressione media $p$

In condizioni di assial-simmetria, la pressione media è definita come

$p = \frac{σ_{1} + σ_{2} + σ_{3}}{3}$
oppure, considerato che in queste condizioni $σ_{1} = σ_{v}$ e $σ_{2} = σ_{3} = σ_{h}$
$p = \frac{σ_{v} + 2 σ_{h}}{3}$

Sforzo deviatorico

sforzo deviatorico $q$

$q = σ_{1} - σ_{3}$
oppure, considerato che in queste condizioni $σ_{1} = σ_{v}$ e $σ_{2} = σ_{3} = σ_{h}$
$q = σ_{v} - σ_{h}$

Modelli Elastici

modelli elastici

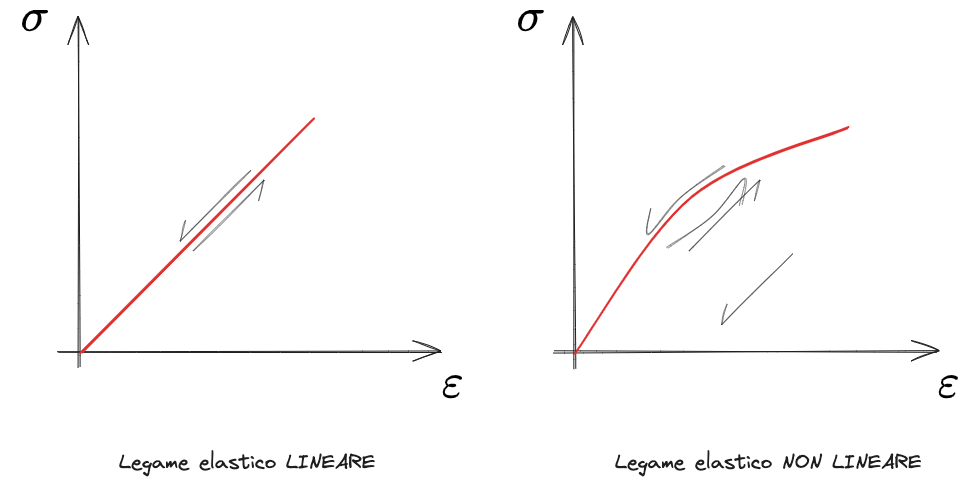
I legami costitutivi che ammettono la completa reversibilità delle deformazioni si dicono legami elastici.

Modello elastico lineare isotropo

modello elastico lineare isotropo

Il modello elastico lineare isotropo ha le seguenti caratteristiche:

Elasticità - completa reversibilità delle deformazioni
Linearità del legame tensioni deformazioni
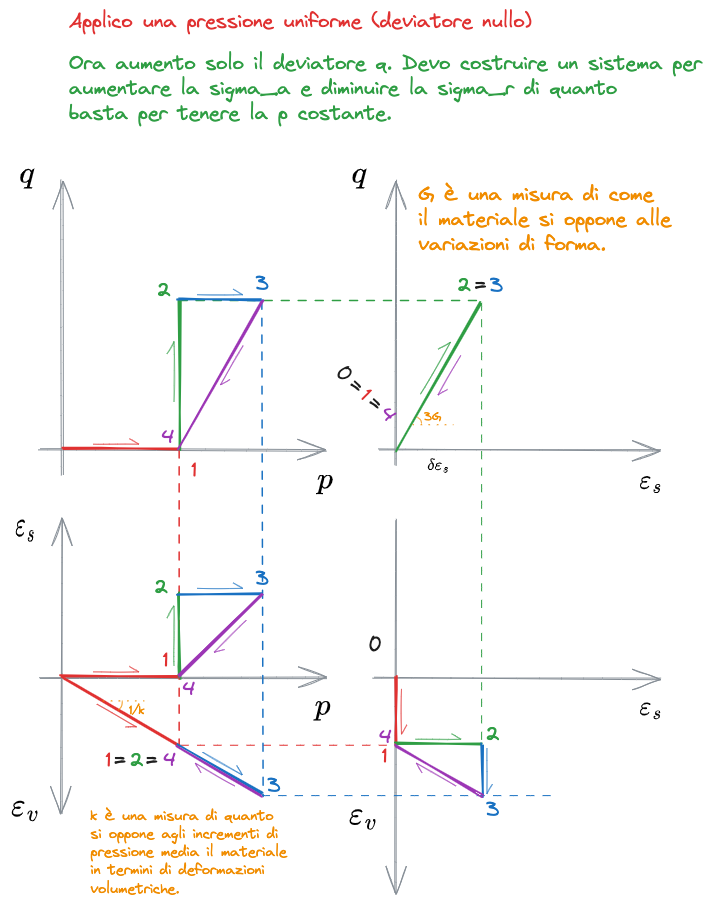
Disaccoppiamento degli effetti prodotto da incrementi di [[#Pressione media]] e quelli prodotti da incrementi degli [[#Sforzo deviatorico]]
- Incrementi di stato di sforzo isotropi producono esclusivamente deformazioni volumetriche
- Incrementi di deviatore producono esclusivamente distorsioni

Se i parametri variano con lo stato tensionale, il modello sarà Elastico NON lineare.

Nella condizione in cui

{\begin{cases} δ σ_{1} = δ σ_{2} = δ σ_{3} \\ δ p \neq 0 \\ δ q = 0 \end{cases} ⟹ {\begin{cases} δ ε_{v} \neq 0 \\ δ ε_{s} = 0 \end{cases}

si avranno solamente deformazioni di volume $δ ε_{v}$ e nessuna di forma $δ ε_{s}$ .

Viceversa, nella condizione in cui:

{\begin{cases} δ p = 0 \\ δ q \neq 0 \end{cases} ⟹ {\begin{cases} δ ε_{v} = 0 \\ δ ε_{s} \neq 0 \end{cases}

Si avranno deformazioni di volume nulle e deformazioni di forma non nulle.

legame elastico lineare isotropo

In generale, il modello elastico lineare isotropo è descritto come segue
$
\begin{bmatrix}
\delta \varepsilon_{v} \
\delta \varepsilon_{s}
\end

\begin{bmatrix}
\frac{1}{K} & 0 \
0 & \frac{1}{3G}
\end{bmatrix}
\begin{bmatrix}
\delta p \
\delta q
\end{bmatrix}
$
dove

$G =$ [[#Modulo di taglio]]
$K =$ [[#Modulo di compressibilità volumetrica]]

Si può scrivere per componenti:

{\begin{cases} δ ε_{v} = \frac{1}{K} δ p \\ δ ε_{s} = \frac{1}{3 G} δ q \end{cases}

Modello rigido plastico perfetto

modello rigido plastico perfetto

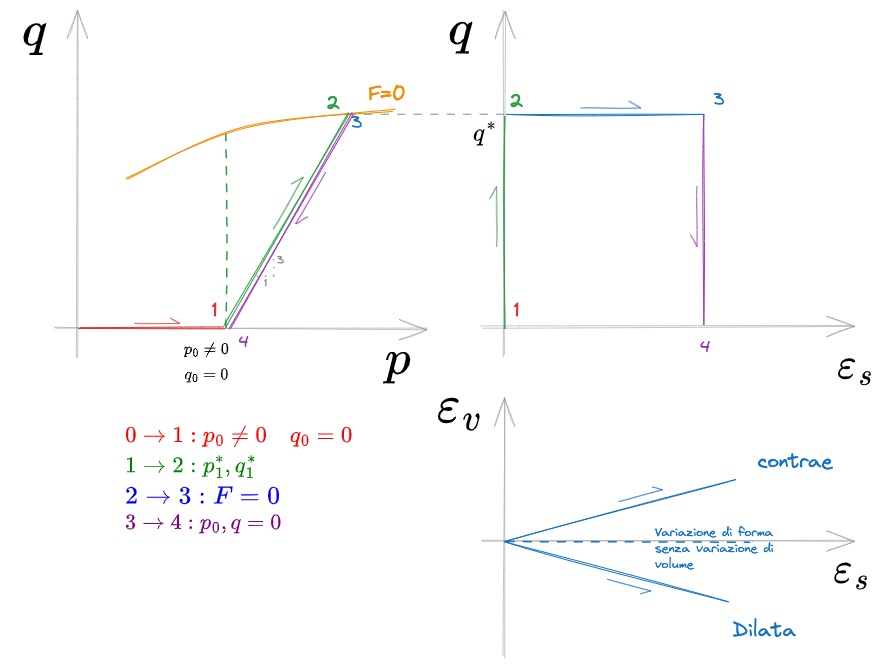
Un corpo rappresentato da un modello rigido plastico perfetto è caratterizzato dalla totale assenza di deformazioni fino al raggiungimento delle condizioni di plasticizzazione (snervamento) - ossia quando la [[#Funzione di Snervamento]] $F = 0$ .

A questo punto si sviluppano deformazioni volumetriche e deviatoriche di natura irreversibile.

Tutta l'energia che viene fornita al sistema, viene dispersa in attrito.
Non è prevista nessuna deformazione reversibile.

Rigido: Fino a un certo carico limite, non c'è deformazione
Plastico: Una volta che il corpo si deforma, non c'è ritorno di deformazione - rimane com'è

Si realizza ora un percorso di carico a controllo di deformazioni su un materiale rigido plastico perfetto

[?] Perché dobbiamo operare a controllo di spostamento e non possiamo operare a controllo di carico?

Funzione di Snervamento

funzione di snervamento ($f$)

La funzione di snervamento $F$ - o funzione di plasticizzazione - rappresenta il luogo dei punti sul piano p-q oltre il quale, lo stato tensionale dato porta il campione a deformarsi.
Stati tensionali che ricadano al di sotto della FdS non causano alcuna deformazione.
La FdS rappresenta la legge di resistenza del materiale.
$F (q, p, h_{1}, h_{2}, . . .) = 0$
Essa è quindi funzione dello stato tensionale ( $q, p$ ) e di alcuni parametri propri del materiale ( $h_{1}, h_{2}$ ).

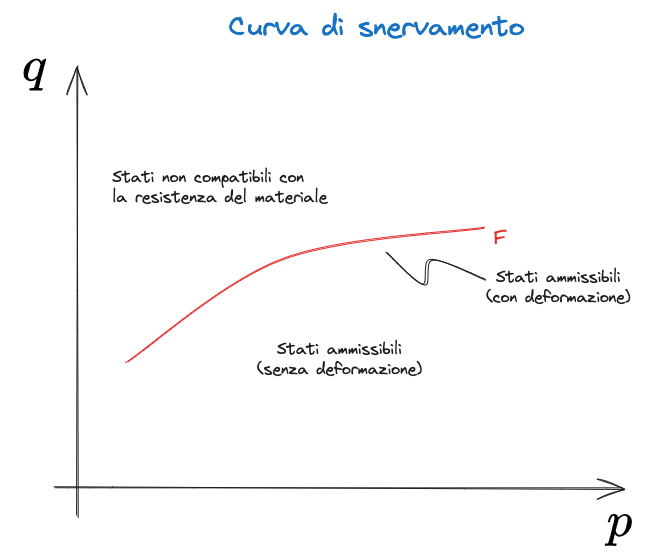
[?] Cosa succede se applico uno stato tensionale per cui mi trovo al di sopra di $F$ ?

La funzione di snervamento ammette l'esistenza di un #Potenziale plastico.

Potenziale plastico

f (q, p, m) = 0

$f$ è funzione di

Stato tensionale ( $p, q$ )
parametro $m$

Questa funzione è tale che, a meno di una costante ( $δ λ$ - moltiplicatore plastico), derivata in $p$ o $q$ fornisce gli incrementi di deformazioni rispettivamente volumetriche e deviatoriche:

{\begin{cases} δ ε_{v}^{p} = δ λ \frac{\partial f}{\partial p} \\ δ ε_{s}^{p} = δ λ \frac{\partial f}{\partial q} \end{cases}

queste sono le componenti della così detta #Legge di flusso

Legge di flusso

La legge di flusso è una funzione che mette in relazione l'incremento di deformazioni plastiche con il gradiente del #Potenziale plastico

δ ε^{p} = δ λ \frac{\partial f}{\partial σ} = δ λ \nabla f

dove

$δ ε^{p} =$ Vettore incremento deformazione plastica
$δ λ =$ Moltiplicatore plastico - descrive l'evoluzione nel tempo delle deformazioni plastiche

osservazioni

È detta legge di flusso perché il corpo si deforma con continuità
Le deformazioni dipendono dallo stato tensionale e da quanto tempo si è in campo plastico ( $δ λ$ )
Il tipo di deformazione NON dipende da $δ λ$ .

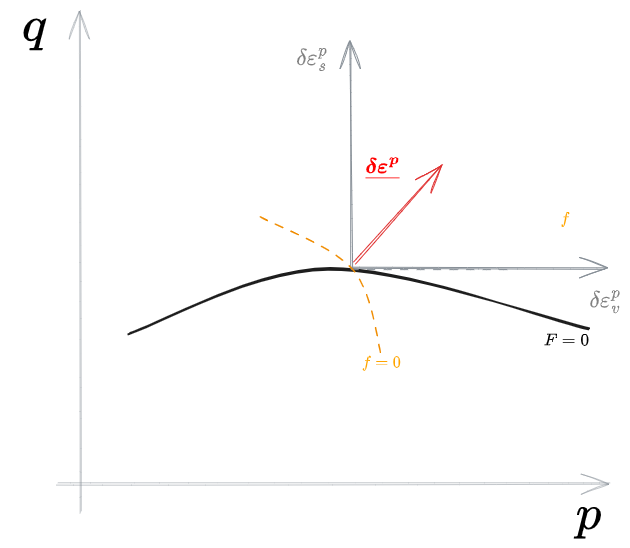
Il #Potenziale plastico permette di rappresentare in modo più compatto lo stato di tensioni e deformazioni del campione, rappresentando tutto su un unico piano.
Si può infatti rappresentare $δ ε^{p}$ in un sistema di riferimento sovrapposto a $p - q$ , riportando le componenti $δ ε_{s}^{p}, δ ε_{v}^{p}$ a partire dal punto rappresentativo dello stato tensionale corrente.
Essendo $δ ε^{p} = δ λ \nabla f$ il gradiente di $f$ , si deve avere perpendicolarità tra le due:

δ ε^{p} ⊥ F f = F

nel punto corrispondente.

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗

Modello elasto-plastico incrudente

[?] Non ci ho capito nulla
[?] Cos'è la superficie di plasticizzazione rispetto alla Funzione di plasticizzazione??

modelli incrudenti

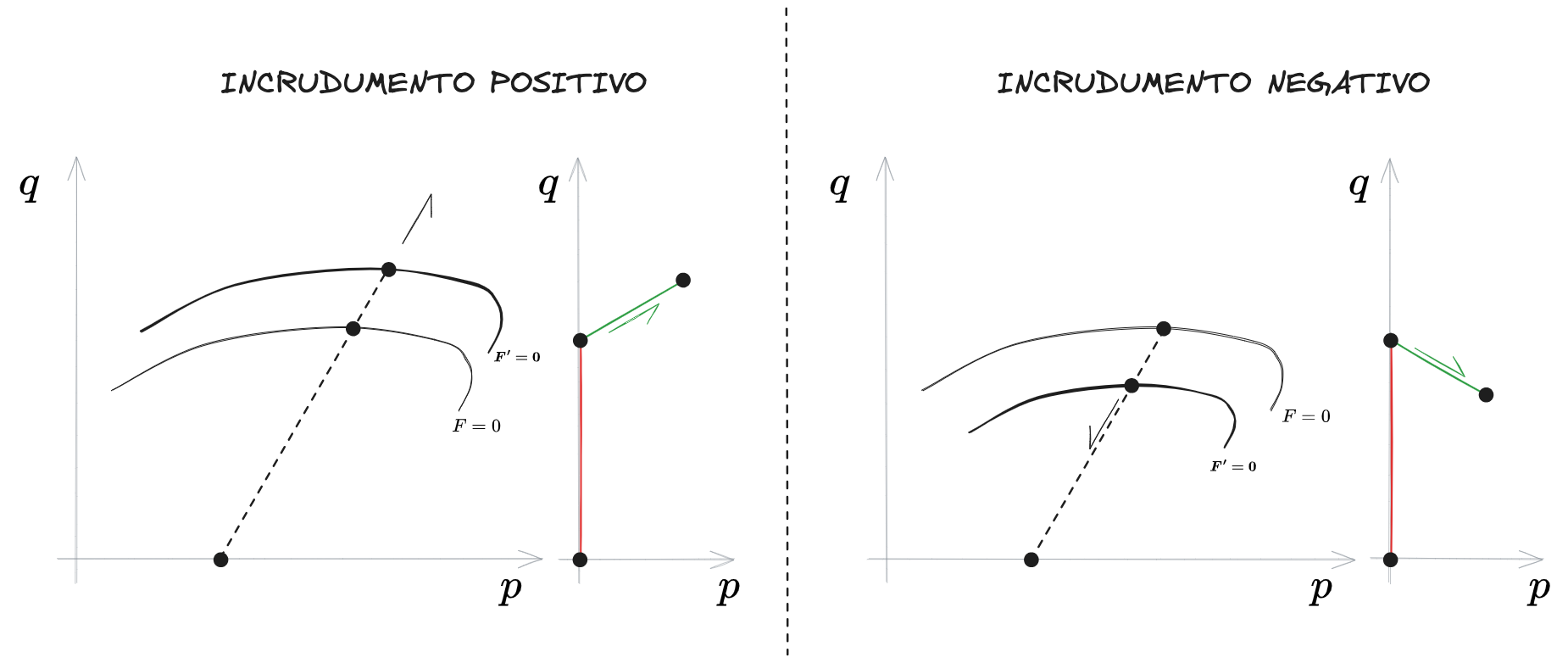
I modelli incrudenti sono una famiglia di modelli costitutivi caratterizzati da un'evoluzione della [[#Funzione di Snervamento]] $F = 0$ al manifestarsi delle deformazioni irreversibili ( $δ ε^{p}$ ).

Si parla di incrudimento POSITIVO quando

la soglia plastica cresce
Il campo plastico si ingrandisce
ossia quando $F$ sale.

Si parla al contrario di incrudimento NEGATIVO quando

la soglia plastica decresce
Il campo plastico si riduce
ossia quando $F$ scende.

Postulato della consistenza

postulato della consistenza

In un processo nel quale si sviluppano deformazioni plastiche (processo di carico plastico), lo stato tensionale corrente deve costantemente soddisfare l'equazione della curva di plasticizzazione corrente.

Come visto nel caso di #Modello rigido plastico perfetto, il modo di deformarsi del materiale è governato dalla #Legge di flusso:

{\begin{cases} δ ε_{v}^{p} = δ λ \frac{\partial f}{\partial p} \\ δ ε_{s}^{p} = δ λ \frac{\partial f}{\partial q} \end{cases}