01. Meccanica del continuo

Siamo interessati allo studio dello stato tensionale dei terreni.

La tensione è una grandezza che rappresenta la forza per unità di superficie, pertanto la misuriamo in

\frac{k N}{m^{2}} = k P a

Ha di fatto le dimensioni di una pressione.

Quando guardiamo a un continuo tri-dimensionale, dobbiamo trovare un modo di rappresentare le tensioni nelle varie direzioni.

Per un punto passano $\infty^{3}$ giaciture.

Ci sono, per ogni giacitura:

2 tensioni tangenziali: $τ_{x}, τ_{y}$
1 tensione normale: $σ$

Per definire lo stato tensionale in uno specifico punto di un continuo, uso il tensore (con 9 componenti).

Definisco la tensione della giacitura $i$ nella direzione $j$ :

τ_{i j} = lim_{δ A \to \infty} \frac{δ F_{i j}}{δ A}

dove $F_{i j}$ è la forza totale applicata sulla giacitura $i$ in direzione $j$ .

In definitiva si avranno quindi 9 componenti:

\begin{aligned} σ_{x} & = lim_{δ A \to \infty} \frac{F_{x}}{δ A} & τ_{y x} & = lim_{δ A \to \infty} \frac{F_{y x}}{δ A} & τ_{z x} & = lim_{δ A \to \infty} \frac{F_{z x}}{δ A} \\ τ_{x y} & = lim_{δ A \to \infty} \frac{F_{x y}}{δ A} & σ_{y} & = lim_{δ A \to \infty} \frac{F_{y}}{δ A} & τ_{z y} & = lim_{δ A \to \infty} \frac{F_{z y}}{δ A} \\ τ_{x z} & = lim_{δ A \to \infty} \frac{F_{x z}}{δ A} & τ_{y z} & = lim_{δ A \to \infty} \frac{F_{y z}}{δ A} & σ_{z} & = lim_{δ A \to \infty} \frac{F_{z}}{δ A} \end{aligned}

da cui otteniamo il #tensore delle tensioni

osservazione

In geotecnica, per convenzione, si considerano positive le tensioni che provocano compressione. Questo perché le terre non possono sviluppare sforzi di trazione.

Tensore delle tensioni

tensore delle tensioni

$σ = [\begin{matrix} σ_{x} & τ_{y x} & τ_{z} x \\ τ_{x y} & σ_{y} & τ_{z y} \\ τ_{x z} & τ_{y z} & σ_{z} \end{matrix}]$
Si dimostra che $τ_{i j} = τ_{j i}$ , per cui il tensore $σ$ è simmetrico.

Al variare del sistema di riferimento, il tensore delle tensioni si modifica

Tensioni principali

Si dimostra che esiste sempre una terna di riferimento tale che le componenti tangenziali siano nulle. In questo caso, il tensore diventa una matrice diagonale:
$σ = [\begin{matrix} σ_{1} & 0 & 0 \\ 0 & σ_{2} & 0 \\ 0 & 0 & σ_{3} \end{matrix}]$

Infine se si ha che $σ_{2} = σ_{3}$ si parla di stato tensionale ortotropo.

Invarianti delle tensioni

Quando descriviamo lo stato di sforzo, è preferibile fare riferimento a delle grandezze invarianti rispetto al sistema di riferimento

invarianti delle tensioni

Sono invarianti rispetto a qualsiasi s.d.r.:

Le tensioni principali e qualsiasi loro combinazione lineare
$I_{1} = tr σ = σ_{1} + σ_{2} + σ_{3}$ La traccia di $σ$
$I_{2} = \frac{1}{2} [(tr σ)^{2} - tr (σ)^{2}] = σ_{1} σ_{2} + σ_{2} σ_{3} + σ_{1} σ_{3}$
$I_{3} = det σ = σ_{1} σ_{2} σ_{3}$ Il determinante di $σ$

Cerchi di mohr

Esercitazione 6 - Diagramma di Mohr Coulomb

Cerchi di Mohr Coulomb

Come costruirlo e a cosa serve

Canale: Marco de Pisapia

Metodo statico di analisi dello stato di tensione --> Cerchio di Mohr
Piano di Mohr.
Ascissa: $σ$
Ordinata: $τ$

Il cerchio di Mohr è un metodo di rappresentazione grafica dello stato tensionale di una roccia o di un terreno.

Dato un generico stato tensionale come in figura

Cerchi di Mohr Coulomb 2023-12-27 12.09.49.excalidraw.png|250

Tale stato di sforzo può essere raffigurato su un piano $τ - σ$ .
La rappresentazione permette di disegnare un cerchio, sulla cui circonferenza devono giacere tutti gli stati di sforzo possibili del provino.

Cerchi di Mohr Coulomb 2023-12-27 12.13.45.excalidraw.png

Si individuano i seguenti punti:

X: Scelta la giacitura- $x$ con $σ$ positivo (compressione), si trova sul piano di Mohr la $τ$ corrispondente
Y: Scelta la giacitura- $y$ con $σ$ positivo (compressione), si trova sul piano di Mohr la $τ$ corrispondente
K: #Polo delle Giaciture - opposto a X
D: #Polo delle normali - opposto a Y

Dal polo delle giaciture è possibile ricavare le direzioni principali di inerzia, ossia le direzioni in cui agiscono esclusivamente sforzi normali.

Polo delle giaciture

polo delle giaciture

Il polo delle giaciture permette di trovare quali tensioni agiscono sulla giacitura corrispondente alla linea che ha origine nel polo e interseca in un altro punto il cerchio di mohr.

Cerchi di Mohr Coulomb 2023-12-27 16.04.02.excalidraw.png

Polo delle normali

Sforzo tangenziale massimo

Sul cerchio di Mohr è possibile individuare il punto di massimo sforzo tangenziale $τ_{m a x}$ .

Cerchi di Mohr Coulomb 2023-12-27 16.28.04.excalidraw.png

Questa individua anche il raggio del Cerchio di Morh:
$r = τ_{m a x} = \sqrt{τ_{x y}^{2} + {(\frac{σ_{x} + σ_{y}}{2})}^{2}}$

Esistono dei diagrammi che permettono di studiare gli stati tensionali di continui 3D per via grafica. In particolare permette di conoscere gli sforzi che agiscono su una giacitura a piacere, dato lo stato dello sforzo.

Tensore delle deformazioni

tensore delle deformazioni

È il tensore:
$ε = [\begin{matrix} ε_{x} & \frac{1}{2} γ_{y x} & \frac{1}{2} γ_{z x} \\ \frac{1}{2} γ_{x y} & ε_{y} & \frac{1}{2} γ_{z y} \\ \frac{1}{2} γ_{x z} & \frac{1}{2} γ_{y z} & ε_{z} \end{matrix}]$

Deformazione lineare

ε_{l} = \frac{l_{1} - l_{0}}{l_{0}}

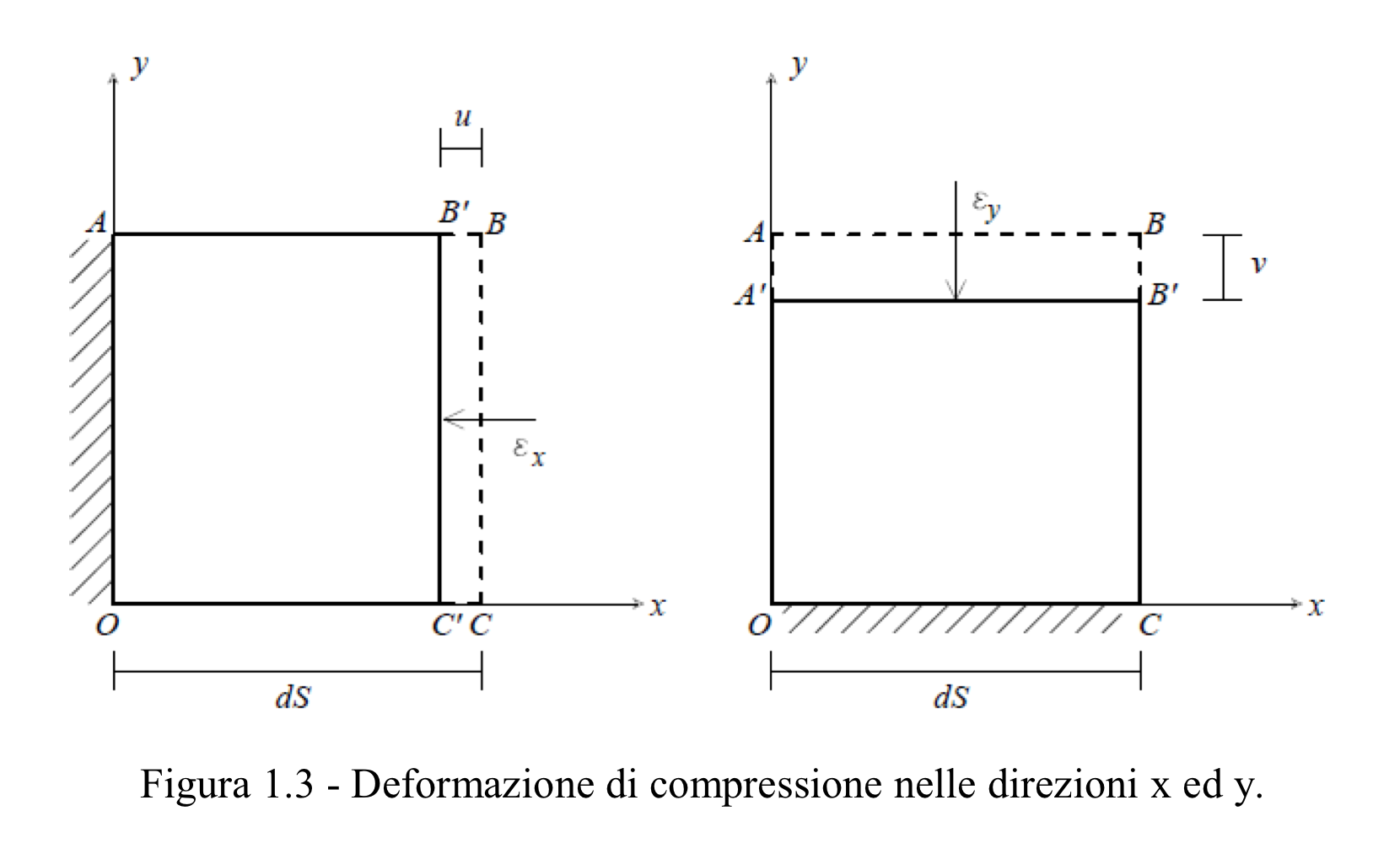
Deformazioni angolari

\begin{aligned} γ_{x y} & γ_{x z} & γ_{y z} \end{aligned}

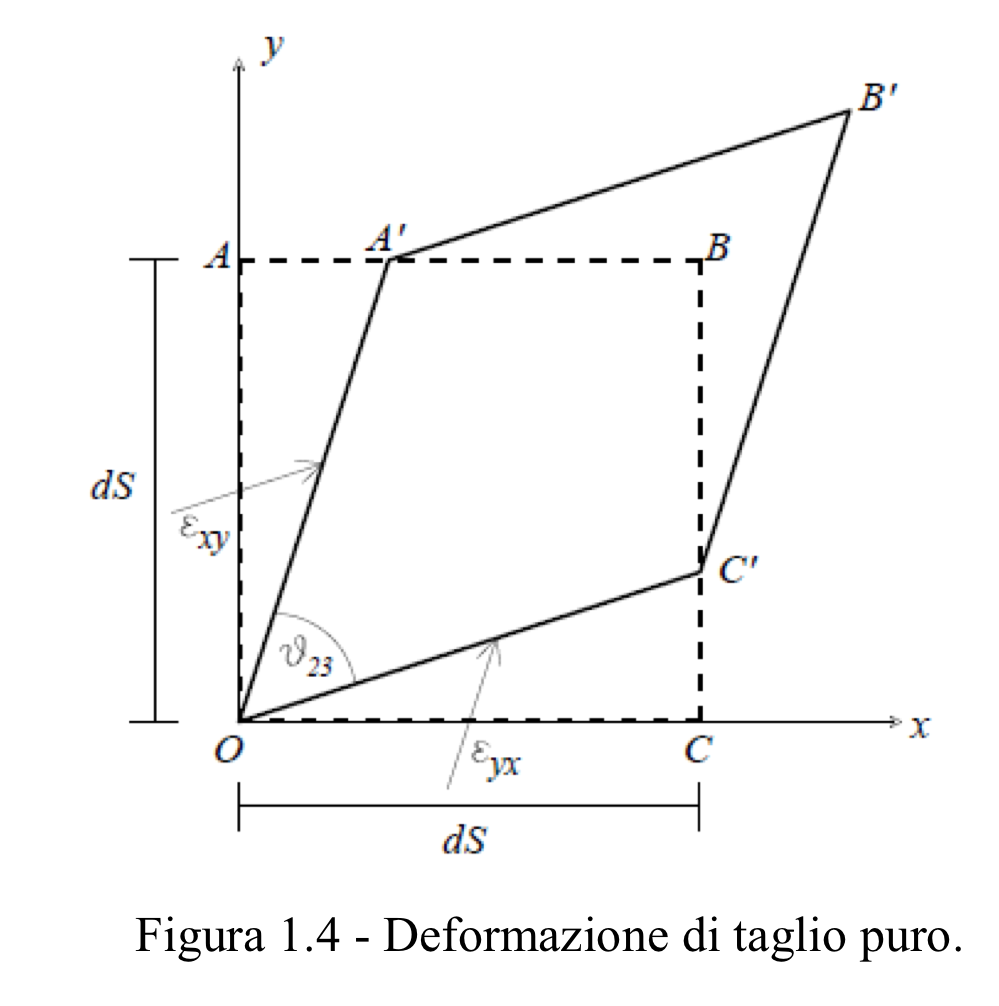
I granuli solidi sono incompressibili. L'acqua che riempie i pori anche, sono incompressibili fisicamente.

L'insieme dei granuli si chiama scheletro solido del terreno.

Trascuriamo lo spazio vuoto, e consideriamo il terreno come un unico solido continuo.
Anche l'acqua è un continuo.

Immagino i due continui sovrapposti.
Ognuno dei due materiali avrà le sue componenti degli sforzi che sovrappongo tra loro.
È il principio dei continui sovrapposti.

È necessario stabilire le leggi con cui gli stati tensionali si distribuiscono tra questi due continui.

Il liquido avrà una pressione interstiziale che è unica per tutto il composto.

Prima di questo principio la meccanica delle terre era un marasma perché nessuno sapeva che tensione pigliare.

principio delle tensioni efficaci

Dato uno stato tensionale in un punto del mezzo: uno stato tensionale totale, con terna principale:
$σ = [\begin{matrix} σ_{1} & 0 & 0 \\ 0 & σ_{2} & 0 \\ 0 & 0 & σ_{3} \end{matrix}]$
Se in quello stesso punto, nell'acqua insiste una pressione interstiziale $u$ si definiscono le tensioni efficaci, le differenze tra le tensioni totali e la pressione dell'acqua:
${\begin{cases} σ_{1}^{'} = σ_{1} - u \\ σ_{2}^{'} = σ_{2} - u \\ σ_{3}^{'} = σ_{3} - u \end{cases}$
Queste Tensioni efficaci hanno sede esclusivamente nello scheletro solido

Tutti gli effetti misurabili (deformazioni, variazioni di resistenza...) dipendono solo e soltanto dalle tensioni efficiaci e dalle sue variazioni

Immaginiamo di avere un terreno saturo.
Applichiamo delle perturbazioni.
Il terreno può rispondere in due situazioni limite:

Condizione non drenata
Condizione drenata

Condizioni non drenate

condizioni non drenate

Si parla di condizioni non drenate se durante l'applicazione di un carico, l'elemento di terra si deforma, ma senza variare di massa. Vista l'incrompressibilità di scheletro solido e acqua, si può dire che non c'è variazione di volume.

In questo caso si producono variazioni della tensione, della pressione e di conseguenza della tensione efficace.

L'applicazione di una generica perturbazione, induce in ogni punto del terreno variazioni di tutte le componenti del tensore delle tensioni totali, e della pressione interstiziale (scalare). Si ha per forza di cose che alcune delle componenti dell'incremento del tensore delle tensioni efficaci debbano essere non nulle.

Δ σ^{'} 0 = Δ σ - Δ u

Le condizioni non drenate si verificano nel breve termine in terreni argillosi caratterizzati da permeabilità molto bassa.

esempio - rilevato

Le frecce rosse sono deformazioni.

Se faccio le aree della linea rossa sono uguali sotto e sopra. Quindi c'è stata deformazione senza variazione di volume.

Questo terreno sta rispondendo in condizioni non drenate

Condizioni drenate

Le tensioni interstiziali sono in equilibrio con le condizioni al contorno.

Viceversa, se applicando il carico, questo si trasferisce direttamente allo scheletro solido (e quindi non ci sono variazioni di pressione ( $u$ ) le variazioni di tensioni efficaci sono tutte identicamente pari alle variazioni delle tensioni totali, allora si dice che il mezzo sta rispondendo in condizioni drenate.

In condizioni drenate, subito dopo l'applicazione della perturbazione, non si verificano ulteriori deformazioni nel tempo.

Le condizioni drenate possono anche riferirsi a una specifica situazione senza fare esplicito riferimento ad un'azione perturbante.

Inoltre, per effetto di perturbazioni verificatesi in un passato anche molto lontano, il sistema può trovarsi in una fase di consolidazione nella quale lo stato deformativo e tensionale stanno ancora evolvendo verso le condizioni drenate di lungo termine

esempio

Un campione di terra si può deformare volumetricamente:

Facendo entrare o uscire acqua.

Se applico un carico e l'acqua non esce (e quindi il volume rimane invariato), la condizione è non drenata: vuol dire che non c'è drenaggio

Se applico un carico e la pressione dell'acqua non varia, la pressione totale comunque aumenta, l'acqua esce e siamo quindi in condizione drenata.

I terreni a grana fine lavorano in condizioni non drenate perché l'acqua ha estrema difficoltà a muoversi.

\begin{array}{r} Δ σ_{v}^{'} = Δ σ_{v} - Δ u \\ Δ σ_{h}^{'} = Δ σ_{h} - Δ u \end{array}

$w_{0} =$ Il cedimento che si verifica a all'istante $t = 0$

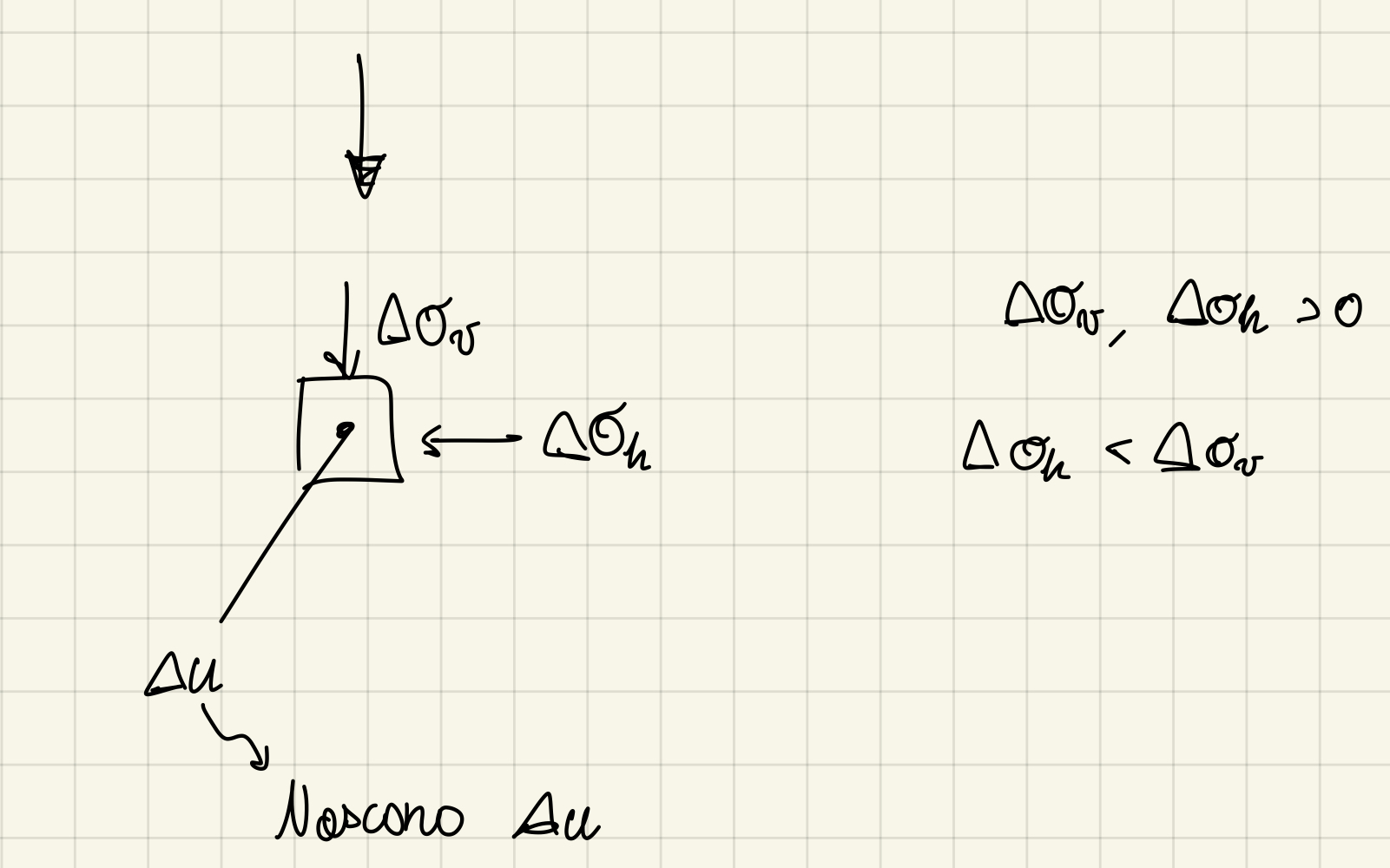
Vediamo a livello fenomenologico cosa succede

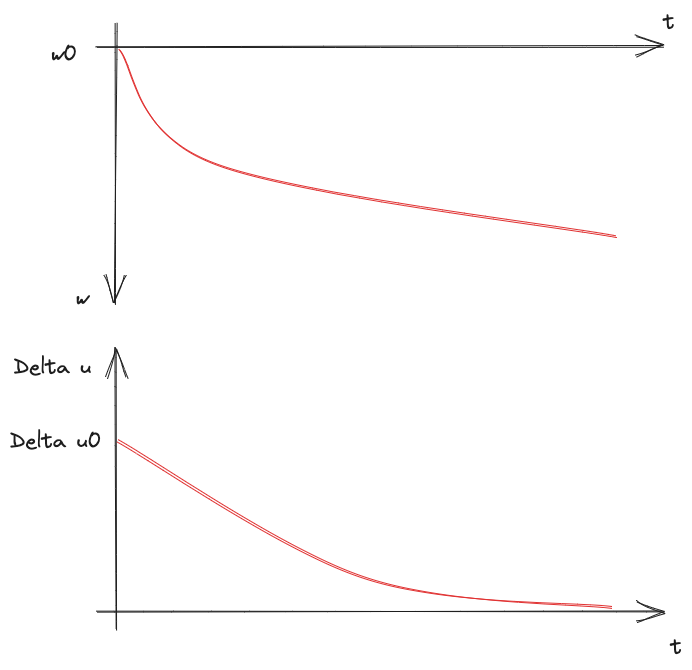
Da $t = 0$ avviene un processo di consolidazione. Da quel momento in poi si entra in condizione drenata. L'acqua in eccesso comincia ad abbandonare i pori.

Non sempre quando costruisco un rilevato si hanno dei cedimenti.
Su un terreno sabbioso, costruisco il rilevato, aumentano le tensioni verticali. L'acqua però non aumenta di pressione. Non nascono $Δ u$ e tutto il carico va sullo scheletro solido. Istante per istante il carico applicato al terreno si trasferisce tutto allo scheletro solido.

Nella risoluzione di un problema di geotecnica, interviene un sistema di 12 incognite e 6 equazioni costituite da

#Equazioni indefinite dell'equilibrio
#Equazioni di compatibilità cinematica
Che per essere risolto richiede altre 6 equazioni che sono fornite dal #Legame costitutivo

Equazioni indefinite dell'equilibrio

(vd. qui e qui, da SDC)

Equazioni indefinite di equilibrio

Fanno riferimento a quello che succede all'interno del continuo in ogni punto del continuo.

Considero un punto generico nel continuo. Considero un infinitesimo nel punto e una generica giacitura. Vediamo le forze che agiscono su quell'elemento.

Sono forze che agiscono sulla superficie. In più, se consideriamo la gravità, ci saranno le forze di volume.

equazioni indefinite di equilibrio

Le equazioni indefinite di equilibrio sono le equazioni nelle varie direzioni che devono essere soddisfatte in conseguenza del fatto che l'elemento si trova in equilibrio.

Si dicono indefinite perché devono essere garantite nella totalità dei punti del continuo. Includono anche l'equilibrio alla rotazione.

${\begin{cases} \frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{y x}}{\partial y} + \frac{\partial τ_{z x}}{\partial z} = 0 \\ \frac{\partial τ_{x y}}{\partial x} + \frac{\partial σ_{y}}{\partial y} + \frac{\partial τ_{z y}}{\partial z} = 0 \\ \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial σ_{z}}{\partial z} = γ \end{cases}$
dove

$γ =$ Peso per unità di volume, che tiene conto degli effetti della gravità lungo l'asse verticale.

Le equazioni indefinite di equilibrio non includono l'equilibrio alla rotazione in quanto queste sono già state usate per ridurre il numero delle componenti del #Tensore delle tensioni da 9 a 6

Le funzioni $σ$ e $τ$ sono continue e derivabili nello spazio.

In queste equazioni ci sono tutte le forze con componenti nelle varie direzioni.

$γ$ è il peso per unità di volume. Nella direzione $z$ infatti conta anche la gravità.

Il peso va considerato perché le terre hanno un comportamento estremamente non lineare nonché plastico.

attenzione

Otteniamo, per vari valori di $F$ e quindi di $σ$ :

Nelle nostre applicazioni è sempre fondamentale tenere conto dello stato tensionale di partenza.
Per capire come mai, guardiamo a una [[Prova Edometrica]]: una prova di "compressione a dilatazione trasversale impedita".

Osserviamo il grafico che otteniamo dalla prova edometrica.

Vediamo come, partendo da uno stato tensionale molto basso (in arancione) e applicando una tensione, si ottiene una deformazione elevata. Al contrario, se partiamo già da uno stato tensionale elevato (in rosso), incrementando la tensione dello stesso valore, otterremo una deformazione molto minore.
Questo non accadrebbe per materiali elastici lineari, dove lo stato tensionale di partenza non conterebbe nulla.

Equazioni di compatibilità cinematica

O equazioni di congruenza

Garantiscono che quando applico dei carichi ad un continuo, questo si deformi.
Nel deformarsi deve succedere che non ci siano:

lacerazioni
compenetrazioni di materia

{\begin{cases} \frac{\partial^{2} ε_{x}}{\partial y^{2}} + \frac{\partial^{2} ε_{y}}{\partial x^{2}} - \frac{\partial^{2} γ_{x y}}{\partial x \partial y} = 0 \\ \frac{\partial^{2} ε_{x}}{\partial z^{2}} + \frac{\partial^{2} ε_{z}}{\partial x^{2}} - \frac{\partial^{2} γ_{x z}}{\partial x \partial z} = 0 \\ \frac{\partial^{2} ε_{y}}{\partial z^{2}} + \frac{\partial^{2} ε_{z}}{\partial y^{2}} - \frac{\partial^{2} γ_{y z}}{\partial y \partial z} = 0 \end{cases}

Tensioni litostatiche

❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ RIFARE/RIVEDERE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗❗
Si immagini di prendere un provino di terra e

Per trovare lo stato tensionale.

Serve $σ_{v 0}$ .
Per definizione:

σ_{v 0} = \frac{W}{δ A} = \frac{γ z δ A}{δ A} = γ z

Se integro la relazione

\frac{\partial σ_{z}}{\partial z} = γ

da cui ottengo

σ_{z} = γ z

e quindi le due corrispondono

Si ha poi che

u = γ_{w} z

La tensione efficace sarà

σ_{v 0}^{'} = σ_{v} - u = γ z - γ_{w} z = (γ - γ_{w}) z

La differenza $γ - γ_{w}$ si chiama peso di volume sommerso ( $γ^{'}, γ_{b}$ ).

TENSIONI ORIZZONTALI

Posso integrare l'equazione:

\frac{\partial σ_{h}}{\partial h} = 0

da cui ottengo

σ_{h} = c o s t

Ci dice che in qualunque direzione l'equilibrio è garantito. Allora non la possiamo usare.
Mi dice però che se mi sposto alla quota $z$ lungo il piano orizzontale, tutte le tensioni, ovunque le calcolo su quel piano, sono uguali.
Usiamo invece delle relazioni empiriche che mettano insieme le tensioni verticali efficaci con le orizzontali efficaci.

σ_{h 0}^{'} = σ_{v 0}^{'} \cdot k_{0}

Dove $k_{0}$ è detto coefficiente di spinta ???
È un numero che è legato alla storia tensionale subita dal deposito.

Se il terreno è un #Terreno normalmente consolidato si ha che

k_{0} = 0, 4 - 0, 6

Se il terreno è un #Terreno sovraconsolidato si ha che

k_{O C} > k_{N C} ≫ 1

Noto $k_{0}$ possiamo conoscere le tensioni orizzontali.

Terreni normalmente consolidati e sovraconsolidati

Terreno normalmente consolidato

Si dice anche terreno vergine.
Se le tensioni litostatiche verticali che ci sono in questo momento sono le massime che il terreno ha subito nella sua storia.

Si definisce il grado di sovraconsolidazione OCR

O C R = \frac{σ_{v m a x}^{'}}{σ_{v 0}^{'}} = 1 ⟹ N C

Terreno sovraconsolidato

Se il terreno, in passato, ha subito tensioni maggiori di quelle presenti al momento della rilevazione.

O C R > 1 ⟹ O C