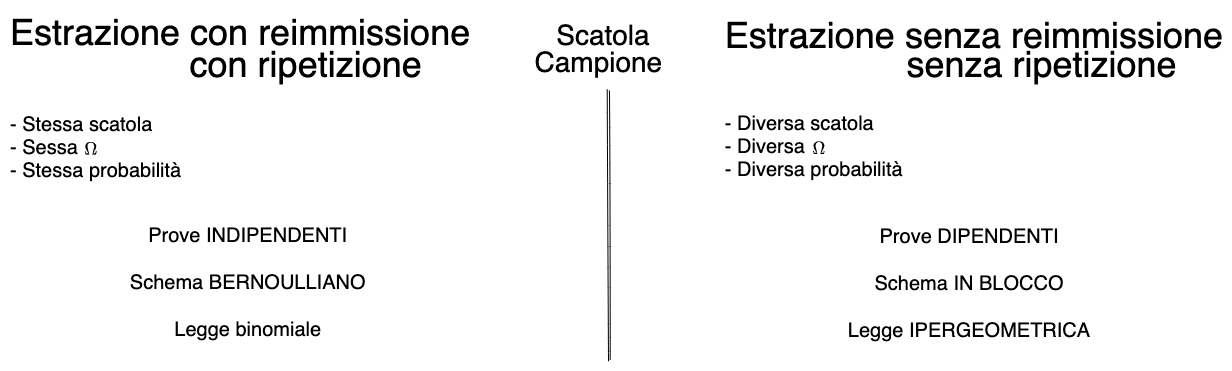
03. Variabili Aleatorie
3. Variabili Aleatorie
In generale, una variabile si dice aleatoria se esiste una distribuzione di probabilità.
Infatti le probabilità possono essere uniformi oppure no
Variabile aleatoria Degenere
Ne deriva che:
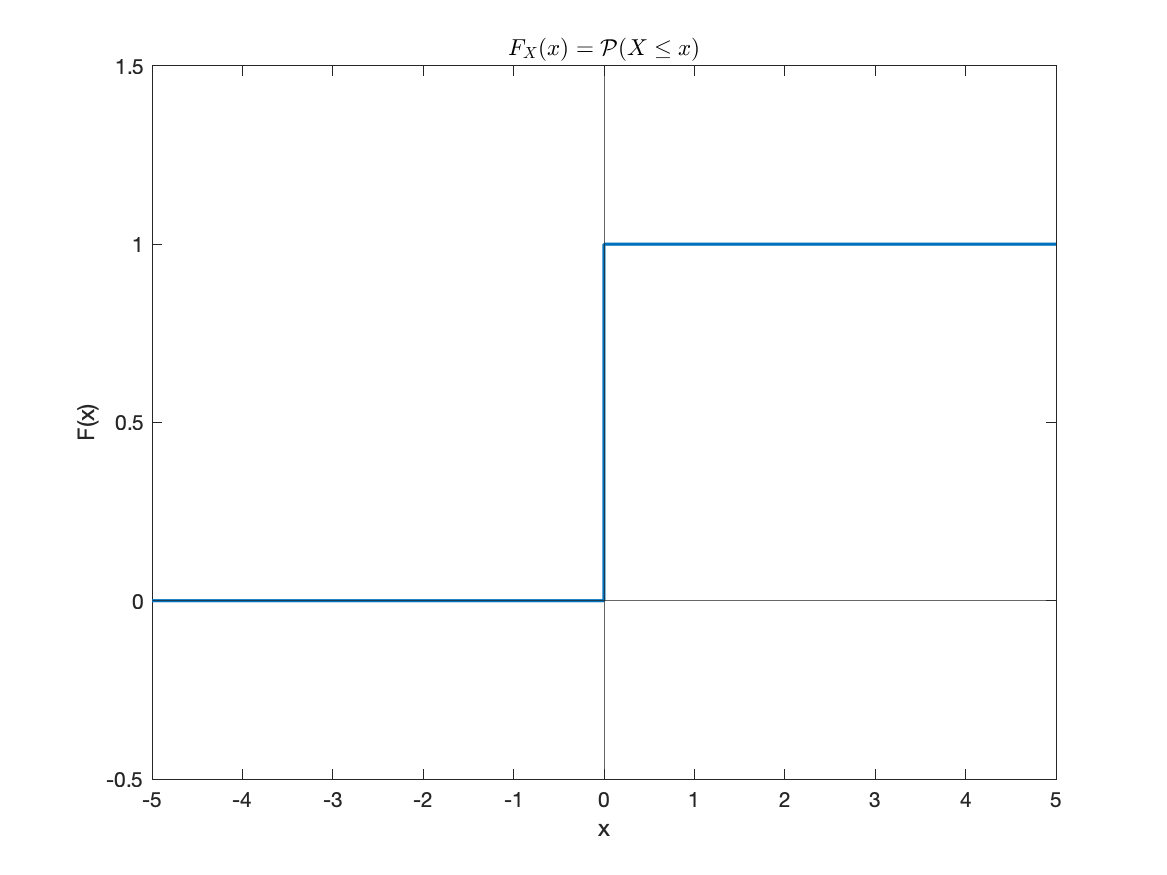
Media
Media di variabili aleatorie Discrete
Sia
Definisco la media di
Ossia la media dei valori di
Media di variabili aleatorie Continue
Proprietà della media
Linearità della media
La media, sia continua che discreta, è lineare:
Dimostrazione
Sia
Per la media di una variabile continua:
Mentre la media di una variabile discreta:
Momento
Il momento di una VA è definito come:
a seconda che
si definiranno:
: Primo momento (coincide con la [[#Media]]) : Secondo momento
Varianza
La varianza è una misura quadratica di quanto
Spesso si indica la varianza con
Facendo alcuni conti:
Da cui vediamo che la varianza è uguale al 2° #Momento meno il 1°:
Deviazione standard
La deviazione standard è ottenuta calcolando la radice quadrata della [[#Varianza]]
La Deviazione standard è poco robusta.
Variabili aleatorie DISCRETE
Condizioni necessarie e sufficienti per densità discreta
La funzione Discreta soddisfa le proprietà 1. e 2. se e solo se è una densità discreta di qualche variabile aleatoria
Tipi di variabili aleatorie discrete
- #Variabile Aleatoria Binomiale
- #Variabile Aleatoria di Bernoulli
- #Variabile Aleatoria Geometrica
- #Variabile Aleatoria di Poisson
Variabile Aleatoria Binomiale
Si dice che
Allora, detto
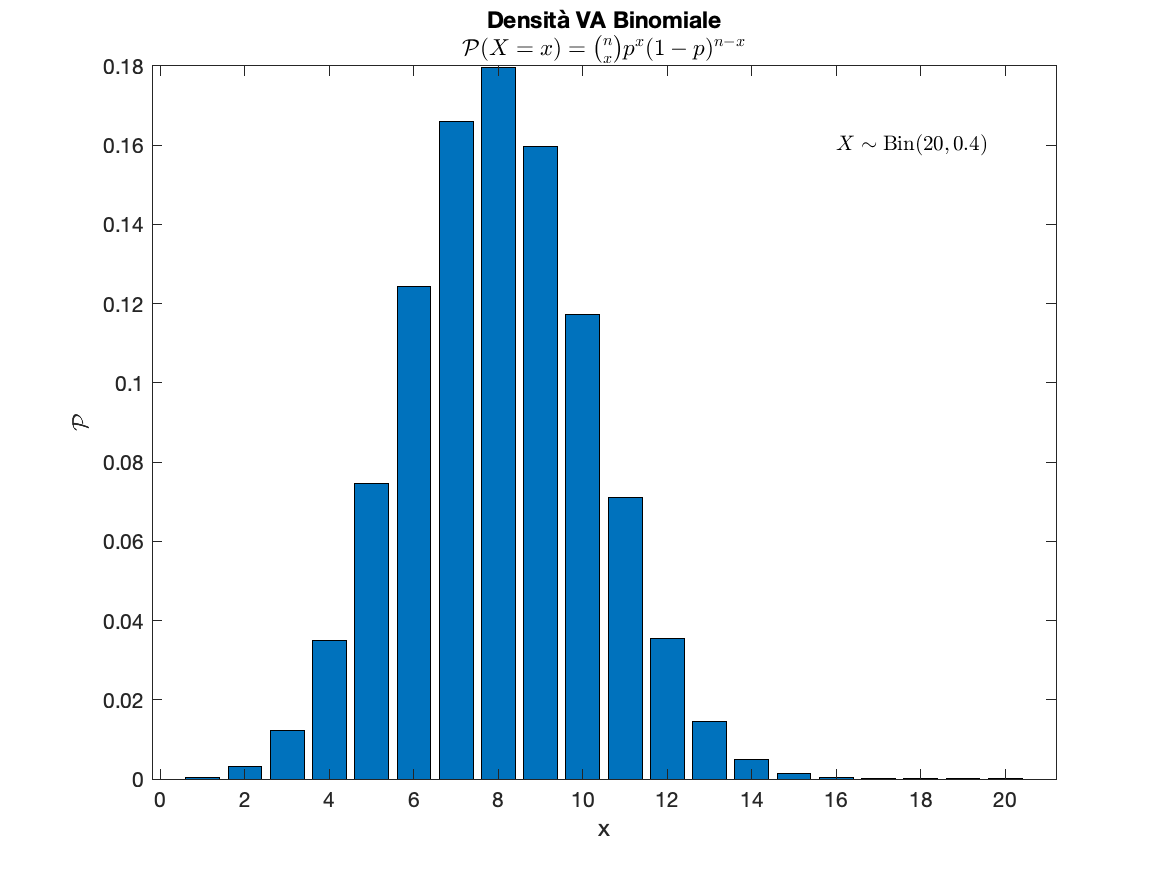
Ricavare la binomiale
Si supponga di avere una scatola contente una pallina con uno 0 e una pallina con un 1. Immagino di voler riempire n caselle con 0 o 1 a seconda della pallina che estraggo, ripetendo l'estrazione n volte con reimmissione
Siano
l'evento: "Ottengo 1, k volte" (lo posso leggere anche come la somma di tutte le caselle) "Valore della casella i-esima"
La probabilità che una qualsiasi casella abbia valore 0, o abbia valore 1, è
La probabilità che, uguale alla probabilità che K = n è:
Proviamo a calcolare la probabilità che:
perché ci sono modi di disporre 2 palline in n caselle. Si tratta infatti di una combinazione semplice di elementi in classe di : .
Generalizzando otteniamo che:
Qualora l'evento considerato non abbia probabilità
Media VA Binomiale
Sia
La #Variabile Aleatoria Binomiale è:
Varianza VA Binomiale
Sia
La #Variabile Aleatoria Binomiale è:
Variabile Aleatoria di Bernoulli
È un caso particolare di [[#Variabile Aleatoria Binomiale]] in cui
con
Media VA di Bernoulli
Sia
La [[#Media di variabili aleatorie Discrete]] per la [[#Variabile Aleatoria di Bernoulli]] è:
Varianza VA Binomiale
Sia
La [[#Varianza]] per la [[#Variabile Aleatoria di Bernoulli]] è:
Variabile Aleatoria Geometrica
con
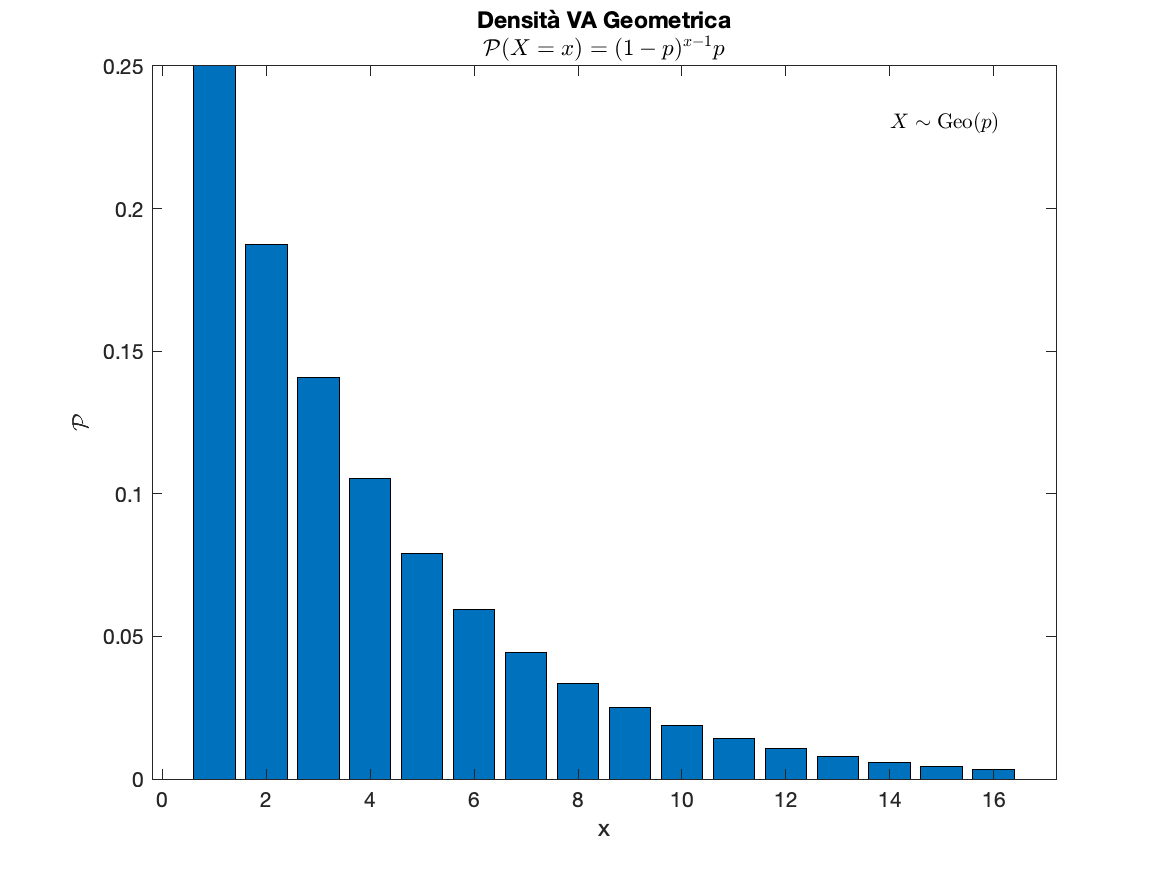
Sia
Media VA Geometrica
Sia
La [[#Media di variabili aleatorie Discrete]] per la [[#Variabile Aleatoria Geometrica]] è:
Dimostrazione:
Per definizione la [[#Media di variabili aleatorie Discrete]] è
Riconosco la serie geometrica
c.v.d.
Dove va a finire il meno?
Una ditta produce lampadine con vita media: 70 accensioni
Una volta installata la lampadina "L" (presa a caso), calcolare
Sia
Sia
e
La media è uguale a 1 fratto la "probabilità che si accenda dopo un certo numero di volte in cui non si è accesa". Il problema richiede la probabilità dell'evento complementare.
Varianza VA Geometrica
Sia
La [[#Varianza]] per la [[#Variabile Aleatoria Geometrica]] è:
Variabile Aleatoria di Poisson
Dato il tasso di successo
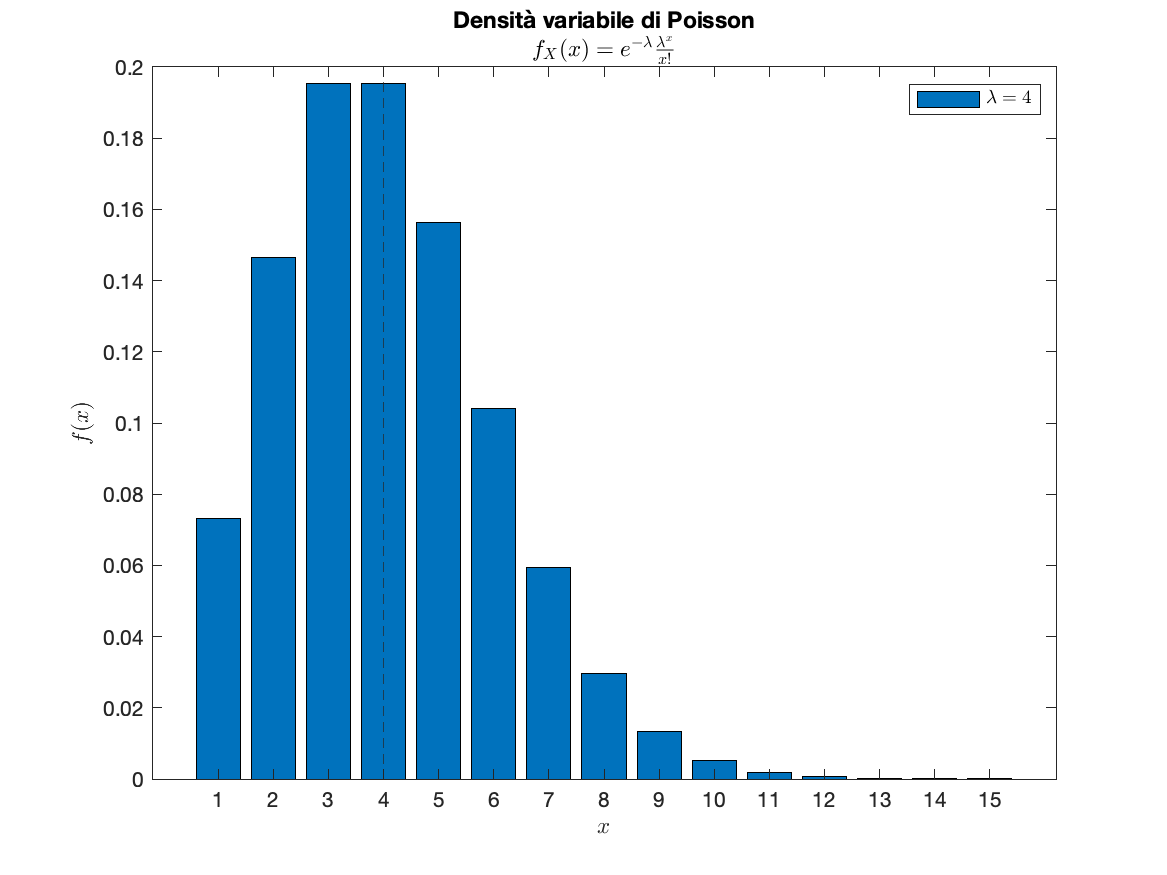
Teoria delle code
La Variabile di Poisson trova applicazione nella teoria delle code. Il Tasso
Media VA di Poisson
Per
Dimostrazione:
Chiamo
In cui riconosco la serie di Taylor Mac-Laurin che converge a
c.v.d.
Da precedenti osservazioni in una banca, si è visto che arrivano mediamente 6 clienti al minuto.
Calcolare
Il tasso di arrivo è di
Di fatto sto chiedendo
Varianza VA Poisson
Sia
La [[#Varianza]] per la [[#Variabile Aleatoria di Poisson]] è:
Variabili aleatorie CONTINUE
Nel mondo reale molte variabili sono continue (il tempo ad esempio). Poi nei fatti noi non siamo in grado di misurare le cose in modo continuo e quindi le osservazioni saranno PUNTUALI (discrete).
Per le variabili aleatorie continue diremo che:
Ci interessa quindi conoscere solo la densità continua
Densità continua
Sia
Definisco il:
Condizioni necessarie e sufficienti per densità continua
La funzione continua soddisfa le proprietà 1. e 2. se e solo se è una densità continua di qualche variabile aleatoria
Supporto
Il supporto di
Inoltre, sia
Dove
Tipi di variabili aleatorie continue
- #Variabile aleatoria Uniforme
- #Variabile Aleatoria Esponenziale
- #Variabile Aleatoria Gamma
- #Variabile Aleatoria Normale o Gaussiana
Variabile aleatoria Uniforme
dove la #Densità continua è
dove
e
Vediamo alcuni casi semplici:
Sia
Calcoliamo
Calcoliamo
Calcoliamo
Essendo
Media VA Uniforme
Sia
La [[#Media di variabili aleatorie Continue]] per la [[#Variabile aleatoria Uniforme]] è:
Varianza VA Uniforme
Sia
La [[#Varianza]] per la [[#Variabile aleatoria Uniforme]] è:
Variabile Aleatoria Esponenziale
Si ritrova spesso nel descrivere la quantità di tempo che passa prima che uno specifico evento accada.
Ad esempio, il tempo, a partire da ora, primo che ci sia un terremoto o che scoppi una nuova guerra, o che una chiamata ricevuta risulti da qualcuno che ha sbagliato numero.
La [[#Densità continua]] è
e
Vediamo alcuni casi semplici:
Calcoliamo
Ricordo
Calcolare
$
\begin
\mathcal{P} (1<X<\frac{3}{2}) &= \int_{1}^{\frac{3}{2}} \lambda e^{-\lambda x}1_{(0, \infty)}(x) , dx = \
&= \left[ -e^{-\lambda x} \right]_{1}^{\frac{3}{2}} = -e^{- \frac{3}{2}\lambda} + e^{-\lambda}
\end{align}
$
Calcolare
Media VA Esponenziale
Sia
La [[#Media di variabili aleatorie Continue]] per la [[#Variabile Aleatoria Esponenziale]] è:
Varianza VA Esponenziale
Sia
La [[#Varianza]] per la [[#Variabile Aleatoria Esponenziale]] è:
Variabile Aleatoria Gamma
Verifichiamo che
Verifico a partire dalla densità
Applico il seguente cambio di variabile:
Da cui
ottengo così
in cui riconosco
Funzione Gamma
La funzione Gamma è la funzione:
Proprietà della funzione gamma
La funzione gamma gode delle seguenti proprietà:
= se
Dimostrazione:
Cominciamo da
c.v.d
Da questo, segue immediatamente la terza affermazione (per
Continuando fino ad ottenere
c.v.d
Media VA Gamma
Dimostrazione
Da
c.v.d.
Varianza VA Gamma
Variabile Aleatoria Normale o Gaussiana
La Variabile Normale si ritrova in moltissime applicazioni pratiche. È stata introdotta inizialmente come approssimazione di una [[#Variabile Aleatoria Binomiale]] per grandi valori del parametro
.
È usata, ad esempio, come distribuzione:
- Dell'altezza di una persona
- Dell'errore nella misura di una quantità fisica
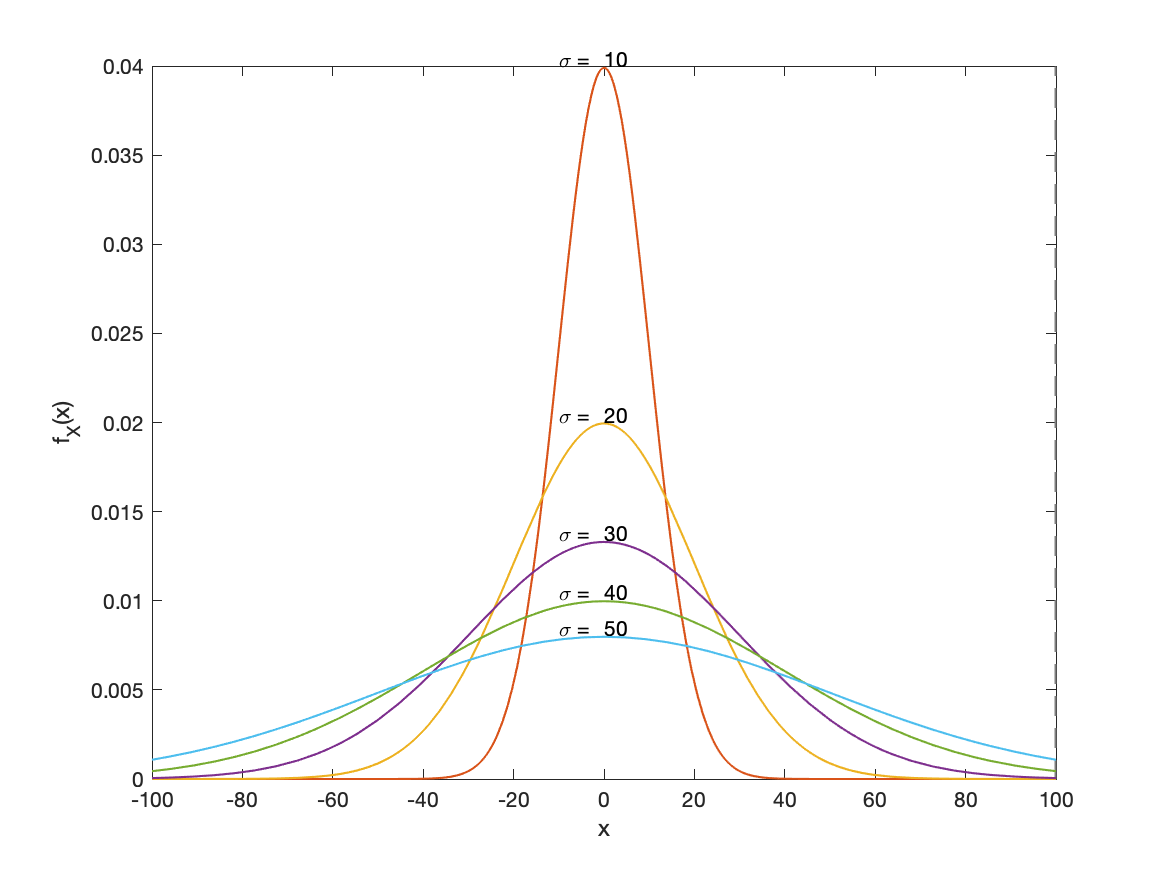
La [[#Densità continua]] è
con
Il [[#Supporto]]:
Per
Verifichiamo che
Moltiplico e divido per la quantità
ottengo
Noto che l'integrale è diventato quello per la probabilità
Per cui rimane
dove
Media VA Normale
Varianza VA Normale
Dimostrazione
c.v.d.
Funzione di Ripartizione
Data
Dall'analisi, per il Teorema Fondamentale del Calcolo Integrale abbiamo
Proprietà della funzione di ripartizione
$
\begin
- &\quad \mathcal{P}(X \in (-\infty,x]) = \mathcal{P}(X \le x) = F_{X}(x) \
- &\quad \mathcal{P}(X \in (x_{1}, x_{2}]) = \mathcal{P}(x_{1}<X\le x_{2}) = F_{X}(x_{2}) - F_{X}(x_{1}) \
- &\quad \mathcal{P}(X \le x_{2}) = F_{X}(x_{1}) + \mathcal{P}(x_{1}<X<x_{2}) \
- &\quad \lim_{x \to \infty} F_{X}(x) = 1 \qquad \qquad \lim_{x \to - \infty}F_{X}(x) = 0 \
- &\quad \lim_{x \to x_{0}^{+}} F_{X}(x) = F_{X}(x_{0}) \qquad \text{(Continuità)}
\end{align}
$
Trasformazioni di variabili aleatorie
È data una variabile aleatoria
Si ha inoltre che
Vogliamo caratterizzare
Se
Sia
Alcune considerazioni:
è continua è continua
Ancheè continua
Per l'esponenziale,
Come primo passo devo trovare
Per
Per cui la [[#Densità continua]] è data da
In
verificato che la funzione sia continua in 0. Ossia