02. Misura e Probabilità
Misura e Probabilità
Funzione indicatrice
La funzione indicatrice è una funzione che ha la seguente forma:
Sia
Probabilità discreta o continua
Probabilità Discreta
Se sfrutta [[#Variabili aleatorie]] discrete. Se, quindi, si lavora in insiemi Numerabili.
Probabilità Continua
Se sfrutta [[#Variabili aleatorie]] continue. Se, quindi, si lavora in insiemi non Numerabili.
Ad esempio il tempo.
Algebre
Una famiglia
Spazio di probabilità
Uno spazio di probabilità è l'insieme
Dove
Insieme eventi elementari " -Algebra indotta da " --> Insieme di tutti gli eventi ai quali possiamo essere interessati Probabilità:
Nell'esempio del dado regolare abbiamo:
Se volessimo calcolare la probabilità che esca un numero
La probabilità che esca un numero pari è invece:
L'insieme di tutti gli eventi ai quali possiamo essere interessati è invece
Si ha poi che:
- #Unione: Dati
- #Intersezione: Dati Dati
- #Passaggio a complementare: Dato
oppure
Un insieme chiuso è un insieme che contiene tutti i suoi punti di accumulazione. La chiusura di un insieme X è il più piccolo insieme chiuso che contiene X.
Un insieme chiuso può avere un numero finito di elementi?
Chiusura rispetto a un'operazione e non rispetto a un altro insieme.
Assiomi
A.1: Gli eventi sono sottoinsiemi di
A.2:
A.3:
A.4: Se
A.5: Se
Classificazione eventi
Certezza di eventi
Evento certo
Evento Impossibile
Eventi complementari
Compatibilità di eventi
Eventi incompatibili
Due eventi
- Non si possono realizzare entrambi
- Sono mutualmente esclusivi
È dato un dado regolare. Gli eventi A e B definiti di seguito sono incompatibili
non può uscire un numero che sia sia pari che dispari:
Dato un insieme finito di eventi
Eventi compatibili
Due eventi
Se due eventi sono compatibili
Legge delle probabilità totali
Siano
Indipendenza di eventi
Due eventi
oppure se
Se
Se due eventi sono incompatibili, la probabilità che si verifichino insieme è nulla.
Eventi Condizionati
A è condizionato a B:
Legge delle probabilità composte
In generale, dati
Nel caso in cui
Dati 2 insiemi
(L.P.C) (L.P.T. = "Legge delle Probabilità Totali") - Dato un evento
,
Dato un evento(Intersezione con evento certo)
Dati due dadi regolari
- Lancio
e - Sommo le facce uscite
Sapendo che la somma è 3, qual è la probabilità che sia uscito 1?
Mi sto chiedendo:
Per la [[#Legge delle probabilità composte]]
Essendo gli eventi al numeratore incompatibili, la probabilità dell'unione è la somma delle probabilità ([[#Assiomi]]) mentre essendo
per cui:
$
\begin{align}
&= \frac{\mathcal{P}(D_{1} = 1) \cdot \mathcal{P}(D_{2} = 2) + \mathcal{P}(D_{1} = 2) \cdot \mathcal{P}(D_{2} = 1)}{\mathcal{P}(D_{1} + D_{2} = 3)} = \
&= \frac{\frac{1}{6} \frac{1}{6} + \frac{1}{6} \frac{1}{6}}{\mathcal{P}(D_{1} + D_{2} = 3)} = 1
\end
$
Essendo
Dati 2 eventi
LPC: [[#Legge delle probabilità composte]] LPT: [[#Legge delle probabilità totali]] - Intersezione con evento certo: Dato un evento
si ha che
Formula di Bayes
Dati un evento ed un insieme finito di [[#Eventi incompatibili]]
allora:
Dimostrazione:
Per la [[#Legge delle probabilità composte]]
Si ha che
Dall'ipotesi
Essendo
quindi
Sostituendo sopra, otteniamo proprio la Formula di Bayes:
c.v.d.
Una lettura della formula di Bayes può essere data in termini di ipotesi. In particolare, se
Propensi agli incidenti Non propensi agli incidenti
Tra
Tra
Il 30% delle persone è
a) Calcolare la probabilità che un nuovo assicurato abbia un incidente entro il primo anno
$
\begin
P(P_{I}) &= 30% \
P(A|P_{I}) &= 40 % \
P(A|P_{I}^{c}) &= 20% \
P(A) &= ?
\end{align}
$
La probabilità che si realizzi
essendo
$
\begin{align}
P(A) &= P(A \cap [P_{I} \cup P_{I}^{c}]) = \
&= P((A \cap P_{I}) \cup (A \cap P_{I}^{c})) \stackrel{[L.P.T.]}{=} \
&= P(A \cap P_{I}) + P(A \cap P_{I}^{c}) \stackrel{[L.P.C.]}{=} \
&= P(A|P_{I})\cdot P(P_{I}) + P(A|P_{I}^{c})\cdot P(P_{I}^{c}) = \
&= \frac{40}{100} \cdot \frac{30}{100} + \frac{20}{100} \cdot \frac{70}{100} = \frac{26}
\end{align}
$
b) Calcolare la probabilità che una persona che ha avuto un incidente entro l'anno sia propensa agli incidenti.
Regola della catena
Spazi di probabilità uniformi
Uno [[#Spazio di probabilità]] è detto uniforme se gli eventi possibili (finiti) sono equibrobabili, cioè tutti di probabilità data e uguale a
Combinatoria
Permutazioni Semplici
Dato un insieme
- di cardinalità
- che differiscono solo per ordine (ordinati)
formano l'insieme
Inoltre
Ad esempio, l'insieme
si ha inoltre che
Combinazioni semplici
Dato un insieme
- di cardinalità
- che non differiscono per ordine (non ordinati)
formano l'insieme
Ad esempio, l'insieme
Come si calcola la distribuzione di probabilità relativa a
Quindi
Permutazioni con ripetizione
Dato un insieme
- Di cardinalità
(Ne estraggo : li estraggo tutti) - Che differiscono per ordinamento (Ordinati)
- Che non differiscono per numero di elementi uguali (Con ripetizione)
formano
Inoltre, la cardinalità:
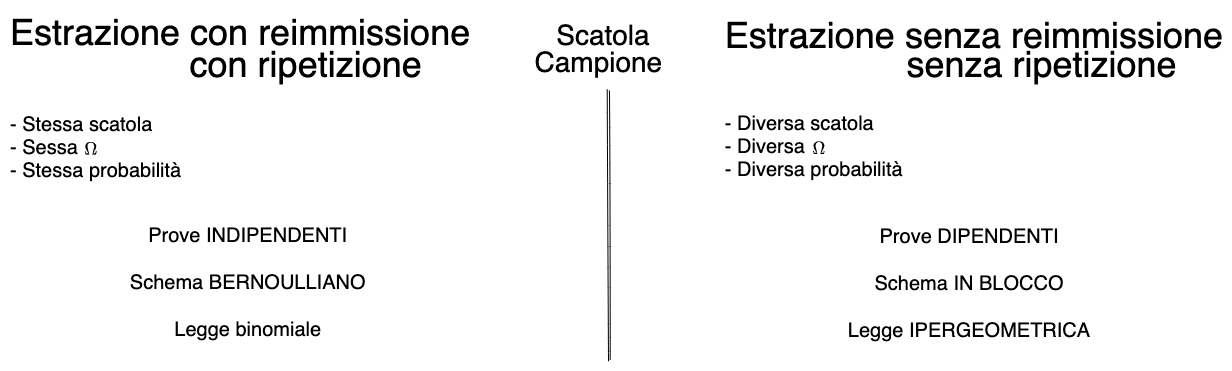
Legge binomiale
con
- 0: Insuccesso
- 1: Successo
Dicotomia (= Può avere 2 valori)
Calcolare la
1: Successo con Testa
0: Insuccesso con Croce
Allora:
Vedi esempi sul quaderno
...
...
...
❗❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ Legge ipergeometrica
❗❗❗❗❗❗❗❗❗❗❗❗❗
27:32 = punteggio : x
x = punt * 32 /27
Ricapitolandolo