01. Osservazione e probabilità

1. Osservazione e probabilità

Statistica descrittiva

statistica descrittiva

La statistica è una scienza, una disciplina, che ha come scopo lo studio quantitativo e qualitativo di fenomeni (non deterministici).
La statistica descrittiva ha lo scopo di fornire una fotografia di una situazione o di un particolare fenomeno osservato.

Una statistica è funzione dei dati campionari

I dati campionari sono costituiti dalle misurazioni (osservazioni) fatte sul campione osservato. Il campione è fatto da unità statistiche selezionate da una popolazione. La popolazione è solitamente l'oggetto di studio finale, del quale si vogliono studiare alcuni fenomeni.

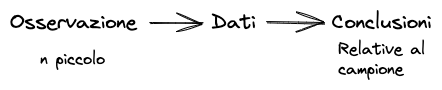
Solitamente ci si basa su un campione limitato di dati ( $n$ piccolo)

esempio

Se volessi calcolare l'altezza media degli italiani dovrei misurare più di 60 milioni di persone. Mi posso però limitare a un gruppo ristretto e usare la [[#Statistica Inferenziale]] per estendere il dato all'intera popolazione.

Misurazioni

Una volta osservato il campione avremo una serie di misurazioni che indichiamo come:

x = (x_{1}, x_{2}, \dots, x_{n})

un vettore di $R^{n}$ di tutte le misurazioni effettuate.

Probabilità

Variabili deterministiche o aleatorie

Variabili deterministiche

variabili deterministiche

Sono variabili $x$ di cui posso conoscere con certezza il valore.

Ad esempio, se lascio cadere un oggetto sul pavimento, in condizioni ideali posso calcolare esattamente il tempo che impiegherà a toccare terra.

Le variabili deterministiche danno vita a modelli deterministici: $f (x, y)$ .

Variabili aleatorie

variabili aleatorie

Sono variabili $X$ di cui NON posso conoscere con certezza il valore.

Ad esempio, se lascio cadere un oggetto sul pavimento, ma è presente un forte vento, non posso conoscere con esattezza il punto in cui cadrà. Posso dire che sicuramente non cadrà a metri di distanza o che cadrà in un punto specifico con una certa probabilità.

Le variabili aleatorie danno vita a modelli aleatori: $g (X, Y)$ .

Possiamo studiare un fenomeno come una variabile aleatoria $X$ di cui non conosciamo il valore fino a che $X$ non si realizza.
Chiamiamo $x$ la realizzazione della variabile aleatoria $X$ . $x \in Ω$ dove $Ω$ è l'insieme di tutte le possibili $x_{i}$ realizzazioni di $X$ .

dado regolare

Se abbiamo un dado regolare, chiameremo la faccia uscita a seguito di un lancio $X$ . La faccia può assumere i valori $x \in Ω$ , dove

$Ω = {1, 2, 3, 4, 5, 6}$

Ci interesserà studiare le seguenti probabilità:

$P (X = x), P (X \leq x), P (X < x), P (X > x), P (X \geq x)$

Eventi certi e impossibili

Evento certo

evento certo

Un evento $X$ che ha probabilità di realizzarsi pari a 1:
$P (X) = 1$

Evento impossibile

evento impossibile

Un evento $X$ che ha probabilità di realizzarsi pari a 0:
$P (X) = 0$

Statistica Inferenziale

Date le osservazioni su un numero $n$ piccolo di misurazioni, mi chiedo come ottenere conclusioni per $n \to \infty$ .
Cioè, voglio ottenere delle informazioni sulla popolazione totale, a partire da un campione della popolazione-

Ottengo così conclusioni sull'Universo.

esempio - componente elettronico

Immaginiamo di voler trovare l'affidabilità di un componente elettronico. Per farlo potrei:

Selezionare $n$ componenti (a caso)
Verificare quanti $k$ di questi funzionano ( $k \in [o, n]$ )
Ottenere $\frac{k}{n}$ componenti funzionanti

$\frac{k}{n}$ è la percentuale di componenti funzionanti. È quindi la probabilità che un qualsiasi componente funzioni. È l'affidabilità.

È chiaro che per $n \to \infty$ il rapporto $\frac{k}{n}$ si deve mantenere costante. Questo è vero se sono rispettate alcune condizioni: Inferenza Statistica.

È importante ricordare che per STIMARE una misura prendendo un campione limitato, devo assicurarmi che gli elementi del campione siano:

Presi a caso
Indipendenti
Queste vanno a costituire le leggi della probabilità.

Il concetto di probabilità

Impostazione classica

Ω finito ⟺ | Ω | < \infty, P (E) = \frac{| E |}{| Ω |}

Impostazione frequentista

$P (E) = lim_{n \to \infty} P (E_{n}) ⟷ n$ prove (ripetute) indipendenti
$n$ deve essere grande a sufficienza, dipende dalla velocità di convergenza.

esempio

Data una moneta. Non so se è regolare. La lancio e registro il risultato. Ripeto $n$ volte (sono prove indipendenti). Se la moneta non è truccata avrò Testa nella metà dei lanci e Croce nell'altra.

Impostazione soggettiva

Si basa su una definizione soggettiva di probabilità: la probabilità di un evento è il prezzo che siamo disposti a pagare in una scommessa per ricevere 1 al verificarsi dell’evento o 0 altrimenti.

Impostazione Bayesana

Fa riferimento alla probabilità condizionata

La probabilità di un evento dipende da una legge a posteriori ottenuta scegliendo (anche soggettivamente) una legge a priori. È forte quindi il condizionamento a ciò che conosciamo sul fenomeno che ci interessa. Si può definire in questo ambito uno schema che prevede aggiornamenti successivi della priori con la posteriori fino ad uno step definito ottimo in qualche senso.

Impostazione Assiomatica

Basato sugli assiomi di Kolmogorov