08. Formule di Quadratura

8. Formule di Quadratura

Il problema consiste nel valutare numericamente degli integrali tipo:

I (f) = \int_{a}^{b} f (x) d x

dove

f (x) : R \to R [a, b] \subset R

In realtà, sono già capace di approssimare la funzione $f$ :

f (x) \approx φ (x)

Posso quindi scrivere:

I (f) = \int_{a}^{b} f (X) d x \approx \int_{a}^{b} φ (x) d x

Occorre comunque una stima dell'errore.

Formule di quadratura interpolatorie

Sia

f (x) = p_{n}^{⋆} (x) + E_{n} (x)

Nodi: ${x_{i}, f (x_{i})}_{0 \leq i \leq n}$

Sia $l_{i} (x)$ il polinomio di Lagrange al nodo $i$ -esimo

p_{n}^{⋆} = \sum_{i = 0}^{n} f (x_{i}) l_{i} (x)

$p_{n} (x_{i}) = f (x_{i})$

Detto ciò, posso riscrivere l'integrale:

\begin{aligned} \int_{a}^{b} f (x) d x & = \int_{a}^{b} p_{n}^{⋆} (x) + E_{n} (x) d x = \\ = \underset{S_{n} (f)}{\underset{⏟}{\int_{a}^{b} p_{n}^{⋆} (x) d x}} + \underset{R_{n} (f)}{\underset{⏟}{\int_{a}^{b} E_{n} (x) d x}} = \end{aligned}

Dove

$S_{n} (f) =$ Parte approssimante
$R_{n} (f) =$ Errore di troncamento

I (f) = S_{n} (f) + R_{n} (f)

con

E_{n} (x) = \frac{\prod_{n} (x)}{(n + 1)!} f^{(n + 1)} (ξ (x))

La parte approssimante è data da:

\begin{aligned} S_{n} (f) & = \int_{a}^{b} \sum_{i = 0}^{n} f (x_{i}) l_{i} (x) d x = \\ = \sum_{i = 0}^{n} f (x_{i}) \underset{c_{i}}{\underset{⏟}{\int_{a}^{b} l_{i} (x) d x}} = \sum_{i = 0}^{n} f (x_{i}) c_{i} \end{aligned}

Dove i $c_{i}$ sono i [[#Coefficienti della Formula di Quadratura]].

FORMULE CHIUSE: $x_{0} = a, x_{n} = b$
FORMULE APERTE: $x_{i} \in (a, b) 0 \leq i \leq n$

Errore di propagazione

L'errore di propagazione si presenta quando è presente un errore nei dati iniziali. Si può quindi scrivere:

y_{i} = f (x_{i}) + ε_{i}

Il polinomio di Lagrange non sarà più $p_{n}^{⋆} (x)$ ma $p_{n} (x)$

p_{n} (x) = \sum_{i = 0}^{n} y_{i} l_{i} (x) = \sum_{i = 0}^{n} (f (x_{i}) + ε_{i}) l_{i} (x)

Per cui posso scrivere l'integrale come:

I (f) = \int_{a}^{b} p_{n} (x) d x = \underset{S (f)}{\underset{⏟}{\sum_{i = 0}^{n} f (x_{i}) \int_{a}^{b} l_{i} (x) d x}} + \sum_{i = 0}^{n} ε_{i} \underset{c_{i}}{\underset{⏟}{\int_{a}^{b} l_{i} (x) d x}}

Per cui definisco la quantità errore di propagazione

R_{n}^{⋆} (f) = \sum_{i = 0}^{n} ε_{i} c_{i}

In definitiva, l'integrale può essere approssimato come:

I (f) = \int_{a}^{b} f (x) d x = S_{n} (f) + R_{n} (f) + R_{n}^{⋆} (f)

Formule di interpolazione chiuse

Nodi equispaziati: $x_{i} = a + i h 0 \leq i \leq n$
$h = \frac{b - a}{n}$
Nodi Gaussiani: Zeri di polinomi ortogonali

Formule di Newton-Cotes

Consiste nel riscrivere $f (x) = p_{n} (x) + E_{n} (x)$ con $p_{n}$ tale che $p_{n} (x_{i}) = f (x_{i}) 0 \leq i \leq b$ .

Sia $q_{m} (x) \in P_{m}$ .

\int_{a}^{b} q_{m} (x) d x = \int_{a}^{b} p_{n}^{⋆} (x) d x + \int_{a}^{b} E_{n} (x) d x

dove l'ultima . uantità è uguale a 0 se $0 \leq m \leq n$ . In questo caso, l'interpolazione è esatta.

Vediamo cosa succede per $m = 0$
$q_{0} (x) = 1$ : il polinomio è una costante.

\begin{aligned} \int_{a}^{b} q_{0} (x) d x & = \int_{a}^{b} p_{n}^{⋆} (x) = \\ b - a & = \int_{a}^{b} \sum_{i = 0}^{n} f (x_{i}) l_{i} (x) d x \\ b - a & = \sum_{i = 0}^{n} q_{0} (x_{i}) c_{i} \\ b - a & = \sum_{i = 0}^{n} c_{i} \end{aligned}

Adesso generalizziamo:
Uso un polinomio di grado $m$ : $q_{m} \in P_{m}$ Con interpolazione esatta, per cui: $0 \leq m \leq 2 n + 1$ .
Sia $Q (x)$ un polinomio:

Q (x) = {(Π_{n} (x))}^{2} = (x - x_{0})^{2} (x - x_{1})^{2} \dots (x - x_{n})^{2} \in P_{2 n + 2} ⟹ Q (x_{i}) = 0 0 \leq i \leq n

Per le considerazioni fatte per $m = 0$ ottengo:

0 < \int_{a}^{b} Q (x) d x = \sum_{i = 0}^{n} Q (x_{i}) c_{i} + R_{n} Q = R_{n} (Q)

essendo $Q (x_{i}) = 0 0 \leq i \leq n$

Grado di Precisione

grado di precisione ($\nu$)

$\begin{aligned} ν & = n & se & n + 1 è pari \\ ν & = n + 1 & se & n + 1 è dispari \end{aligned}$

Formula del Trapezio (n=1)

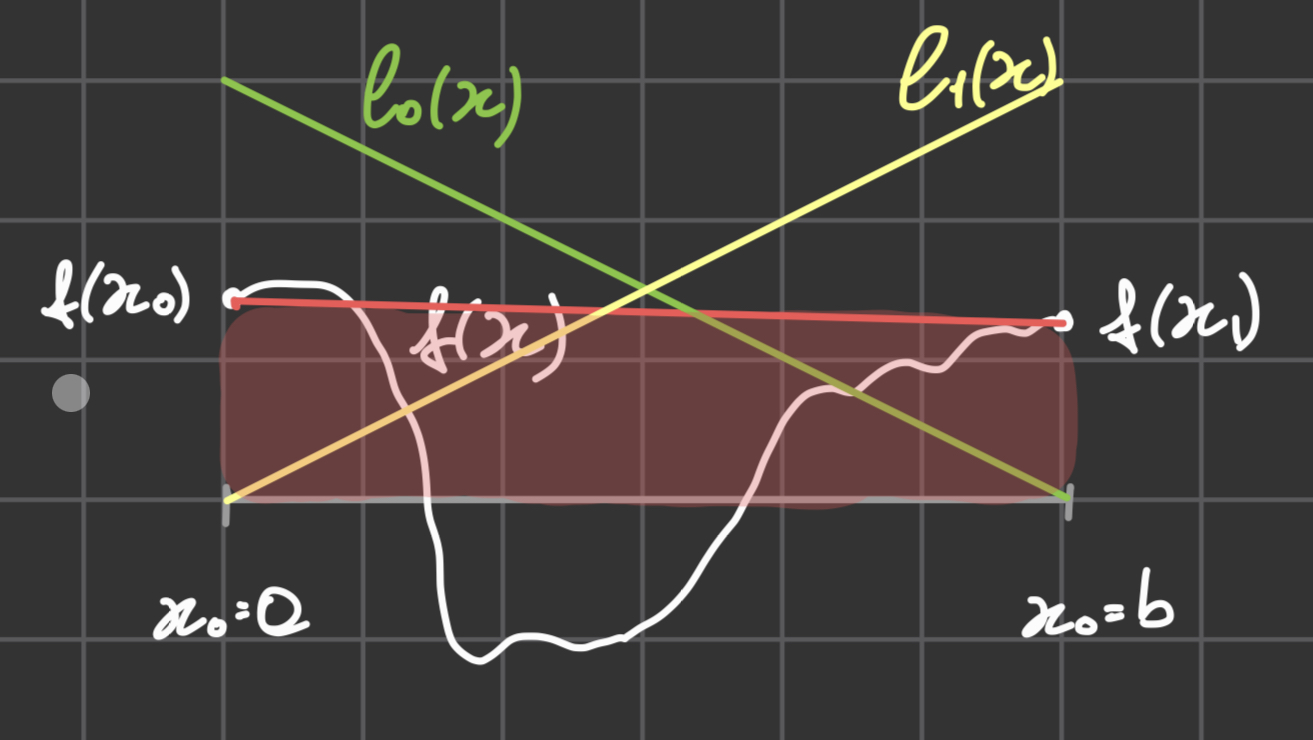
La formula del Trapezio è una Formula di Newton-Cotes quando $n = 1$

nodi: $x_{0} = a, x_{1} = b$
[[#Grado di Precisione]]: $ν = 1$ : resto è zero per tutti i polinomi fino al grado 1.

Il polinomio è:

\begin{aligned} p_{1} & = f (x_{0}) l_{0} (x) + f (x_{1}) l_{1} (x) \\ = f (a) \frac{x - x_{0}}{x_{0} - x_{1}} + f (b) \frac{x - x_{1}}{x_{1} - x_{0}} \\ = f (a) \frac{x - a}{a - b} + f (b) \frac{x - b}{b - a} \end{aligned}

Calcolo i [[#Coefficienti della Formula di Quadratura]] $c_{i}$ :

\begin{aligned} c_{0} & = \int_{a}^{b} l_{0} (x) d x = \int_{a}^{b} \frac{x - b}{a - b} d x = \frac{b - a}{2} \\ c_{1} & = \int_{a}^{b} l_{0} (x) d x = \int_{a}^{b} \frac{x - a}{b - a} d x = \frac{b - a}{2} \end{aligned}

Per cui la parte approssimante è:

\begin{array}{r} S_{1} (f) = \sum_{i = 0}^{n} f (x_{i}) c_{i} = f (a) \frac{b - a}{2} + f (b) \frac{b - a}{2} = \frac{b - a}{2} (f (a) + f (b)) \end{array}

Ossia approssimo l'area sotto la funzione con l'area sotto il trapezio

L'errore è invece dato da

R_{1} (f) = \int_{a}^{b} E_{n} (x) d x = \int_{a}^{b} \frac{(x - a) (x - b)}{2!} f^{″} (ξ (x)) d x \overset{Teo della media}{=} - \frac{1}{12} (b - a)^{3} f^{″} (τ) τ \in [a, b]

Siano:

\begin{array}{r} min_{x \in [a, b]} f^{″} (x) = m \\ max_{x \in [a, b]} f^{″} (x) = M \end{array}

si ha per ogni $x$ :

m \leq f^{″} (x) \leq M

per cui:

\begin{array}{r} - \frac{1}{12} (b - a)^{3} m \leq R_{1} (f) \leq - \frac{1}{12} (b - a)^{3} M se f^{″} (x) < 0 \\ - \frac{1}{12} (b - a)^{3} m \geq R_{1} (f) \geq - \frac{1}{12} (b - a)^{3} M se f^{″} (x) > 0 \end{array}

Formula di Cavalieri-Simpson (n=2)

Nodi:

\begin{aligned} x_{0} & = a \\ x_{1} & = a + \frac{b - a}{2} = \frac{b + a}{2} \\ x_{2} & = a + 2 h = b \end{aligned}

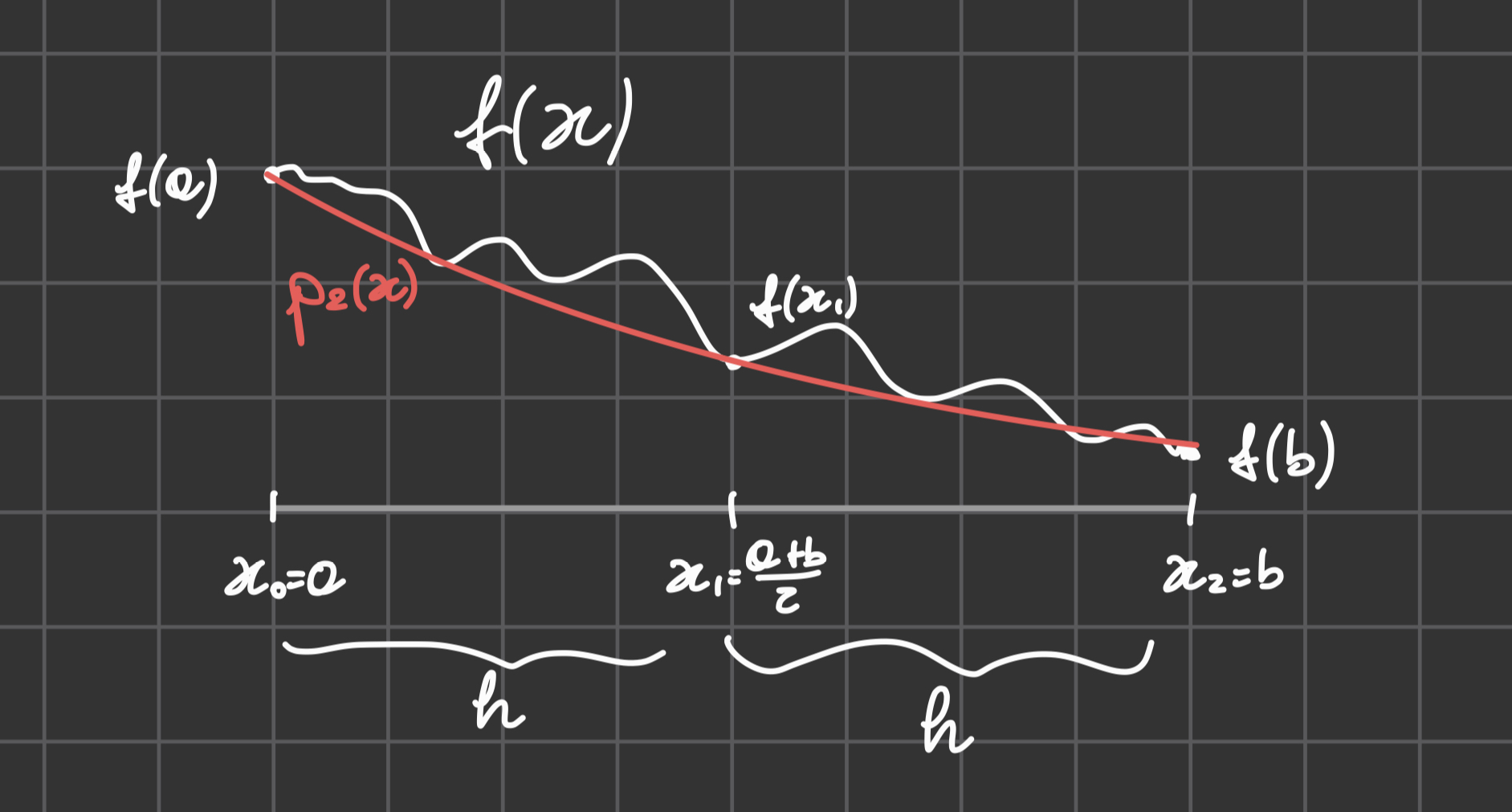
Il polinomio è:

p_{2} (x) = f (x_{0}) l_{0} (x) + f (x_{1}) l_{1} (x) + f (x_{2}) l_{2} (x)

Ricordo:

l_{i} (x) = \prod_{\begin{array}{r} j = 0 \\ i \neq j \end{array}} \frac{x - x_{i}}{x_{i} - x_{j}}

Si ha che la parte approssimante è

S_{2} (f) = \int_{a}^{b} p_{2} (x) d x = \frac{h}{3} (f (a) + 4 f (x_{1}) + f (b))

e l'errore

R_{2} (f) = \int_{a}^{b} E_{2} (x) d x = - \frac{h^{5}}{90} f^{(4)} (τ) τ \in [a, b]

Convergenza

convergenza

Si ha convergenza se:
$lim_{n \to \infty} R_{n} (x) = 0 ⟺ lim_{n \to \infty} S_{n} (f) = I (f)$

teorema

Sia $f \in C [a, b], [a, b]$ limitato, la successione di formule di quadratura ${S_{n} (f)} n = 1, 2, . . .$ tale che
$\sum_{i = 0}^{n} | c_{i} | \leq L \forall n = 1, 2, . . .$
allora
$lim_{n \to \infty} S_{n} (f) = I (f)$

Formule di Newton-Cotes generalizzate

Consiste nell'estendere l'approssimazione dell'integrale da un singolo intervallo, a una serie di intervalli sempre più piccoli, aumentando il numero di nodi, ed ottenendo un'approssimazione più precisa.

Formula del Trapezio generalizzata

T (f) = \frac{h}{2} (f (a) + 2 \sum_{i = 1}^{N - 1} f (x_{i}) + F (b))

| E_{n}^{T O T} (f) | \leq | R_{n} (f) | + | R_{n}^{⋆} (f) |

con

\begin{aligned} R_{n} (f) & = - (\frac{b - a}{12}) h^{2} f^{″} (τ) τ \in [a, b] \\ | R_{n}^{⋆} (f) | & \leq ε (b - a) \end{aligned}

con $ε$ errore sui dati.

Criterio di Runge-Kutta per Trapezi

R_{\frac{h}{2}}^{T} (f) = \frac{1}{3} (T_{\frac{h}{2}} (f) - T_{h} (f))

Formula delle parabole generalizzata

P_{n} (f) = \frac{h}{3} (f (a) + 4 \sum_{j = 0}^{\frac{n}{2} - 1} f (x_{2 j + 1}) + 2 \sum_{j = 0}^{\frac{n}{2} - 1} f (x_{2 j}) + f (b))

con

R_{n}^{p} (f) = - \frac{b - a}{180} h^{4} f^{I V} (τ)

Criterio di Runge-Kutta per Parabole

R_{\frac{h}{2}}^{P} (f) = \frac{1}{15} (P_{h} (f) - P_{\frac{h}{2}} (f))