07. Teoria dell'approssimazione

7. Teoria dell'approssimazione

La teoria dell'approssimazione è una branchia dell'analisi numerica utile ad approssimare una serie di dati con una funzione di qualche tipo.
Può essere divisa in due macroaree:

[[#Approssimazione]]
[[#Interpolazione]]

data fitting

Si hanno delle misurazioni sperimentali dell'allungamento di una molla:

$x$	2	3	4	...	10
$F$	7.0	8.3	9.4	...	15.9

Legge di Hooke:
$F (x) = - k (x - l) = - k x + k l$

type: line
labels: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
series:
  - title: x
    data: [3, 4.5, 7.0,8.3, 9.4, 10.2, 11.4 ,12.8, 14.0, 14.2,15.9 ]
tension: 0.2
width: 80%
labelColors: false
fill: false
beginAtZero: false
bestFit: true
bestFitTitle: undefined
bestFitNumber: 0

interpolazione

Braccio robotico deve fare dei fori.
Dobbiamo comunicare:

Posizione dei fori
Percorso più breve
Uso polinomi a tratti di grado 3 (Spline)

Approssimazione ai minimi quadrati

Sia $φ (x)$ la funzione approssimante
Vogliamo minimizzare la distanza tra i dati e la funzione approssimante.

Calcolo la distanza come norma Euclidea: scarto quadratico
$\sum_{i = 0}^{n} (φ (x_{i}) - y_{i})^{2}$
Voglio minimizzare lo scarto quadratico

osservazione

Posso anche pesare i dati:

\sum_{i = 0}^{n} w_{i} (φ (x_{i}) - y_{i})^{2}

Possibili funzioni approssimanti

Retta

p_{1} (x) = a x + b

2 parametri incogniti: $a, b$

Polinomi algebrici

Per fenomeni regolari dove non prevediamo grosse variazioni

p_{m} (x) = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{m} x^{m}

$m + 1$ parametri incogniti

Polinomi trigonometrici

T_{M} (x) = \frac{a_{0}}{2} + \sum_{k + 1}^{M} (a_{k} \cos (k x) + b_{k} \sin (k x))

$2 m + 1$ parametri incogniti

Funzioni lineari logaritmiche

Funzioni esponenziali

Problema fondamentale

Dato il vettore $Γ$ :
$Γ = [\begin{matrix} γ_{0} \\ ⋮ \\ γ_{M} \end{matrix}]$
di $M + 1$ parametri.

nodi: $x_{0} < x_{1} < \dots < x_{n}$

Lo [[#Scarto quadratico]] è
$σ^{2} = \sum_{i = 0}^{n} (φ (x_{i}) - y_{i}) = \sum_{i = 0}^{n} ((γ_{0} ψ_{0} (x_{i}) + γ_{1} ψ_{1} (x_{i}) + \dots + γ_{M} ψ_{M} (x_{i})) - y_{i})^{2}$
Le incognite sono i parametri $γ$ .

L'obiettivo è minimizzare rispetto ai parametri la funzione:
$σ^{2} = F (γ_{0}, γ_{1}, \dots, γ_{M})$
Procedo al calcolo della derivata:
$\frac{\partial F}{\partial γ_{k}} (γ_{0}, γ_{1}, \dots, γ_{M}) \overset{!}{=} 0 0 \leq k \leq M$
$\frac{\partial F}{\partial γ_{k}} = {\begin{cases} \frac{\partial F}{\partial γ_{0}} = \sum_{i = 0}^{n} (2 (γ_{0} ψ_{0} (x_{i}) + \dots + γ_{M} ψ_{M} (x_{i}) - y_{i}) \cdot ψ_{0} (x_{i})) & \overset{!}{=} 0 \\ \frac{\partial F}{\partial γ_{1}} = \sum_{i = 0}^{n} (2 (γ_{0} ψ_{0} (x_{i}) + \dots + γ_{M} ψ_{M} (x_{i}) - y_{i}) \cdot ψ_{1} (x_{i})) & \overset{!}{=} 0 \\ ⋮ \\ \frac{\partial F}{\partial γ_{M}} = \sum_{i = 0}^{n} (2 (γ_{0} ψ_{0} (x_{i}) + \dots + γ_{M} ψ_{M} (x_{i}) - y_{i}) \cdot ψ_{M} (x_{i})) & \overset{!}{=} 0 \end{cases}$

Distribuendo la sommatoria, ottengo
$\frac{\partial F}{\partial γ_{k}} = γ_{0} \underset{h_{k 1}}{\underset{⏟}{\sum_{i = 0}^{n} ψ_{0} (x_{i}) ψ_{k} (x_{i})}} + \dots + γ_{M} \sum_{i = 0}^{n} ψ_{M} (x_{i}) ψ_{k} (x_{i}) - \sum_{i = 0}^{n} y_{i} ψ_{k} (x_{i}) = 0$
da cui definisco una matrice $H$ , simmetrica:
$H = [\begin{matrix} h_{00} & h_{01} & \dots & h_{0 M} \\ h_{10} & h_{11} & \dots & h_{1 M} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ h_{M 0} & h_{M 1} & \dots & h_{M M} \end{matrix}] \in R^{(M + 1) \times (M + 1)}$
le cui entrate sono:
$h_{i j} = \sum_{i = 0}^{n} ψ_{i} (x_{i}) ψ_{j} (x_{i})$
Posso quindi costruire la matrice $V$ di seguito e porre $H = V^{T} V$ :
$V = [\begin{matrix} ψ_{0} (x_{0}) & ψ_{1} (x_{0}) & \dots & ψ_{M} (x_{0}) \\ ψ_{0} (x_{1}) & ψ_{1} (x_{1}) & \dots & ψ_{M} (x_{1}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ ψ_{0} (x_{n}) & ψ_{1} (x_{n}) & \dots & ψ_{M} (x_{n}) \end{matrix}] \in R^{(n + 1) \times (M + 1)}$

$H$ è definita positiva
$H$ è regolare
Esiste una sola soluzione

Calcolo l'Hessiana
$H_{ess} = {(\frac{\partial^{2} F}{\partial γ_{j} \partial γ_{k}})}_{0 \leq j, k \leq M} = 2 H$
Rispetto alla derivata prima, i $Γ$ tali che la derivata prima fa $0$ sono punti di minimo se:

$det H_{ess} > 0$
$H_{ess}$ è definita positiva

Polinomio Algebrico ai minimi quadrati

Dati: ${x_{i}, y_{i}} 0 \leq i \leq n$

definisco il polinomio:
$\begin{aligned} P_{M} & = a_{0} + a_{1} x + \dots + a_{M} x^{M} \\ = γ_{0} ψ_{0} (x) + γ_{1} ψ_{1} (x) + \dots + γ_{M} ψ_{M} (x) \end{aligned}$

si ha quindi che $ψ_{k} (x) = x^{k}$

gli elementi della matrice $H$ sono:
$h_{j k} = \sum_{i = 0}^{n} ψ_{j} (x_{i}) ψ_{k} (x_{i}) = \sum_{i = 0}^{n} x_{i}^{j} x_{i}^{k} = \sum_{i = 0}^{n} x_{i}^{j + k} \overset{△}{=} s_{j + k}$
Termine noto:
$b_{k} = \sum_{i = 0}^{n} y_{i} ψ_{k} (x_{i}) = \sum_{i = 0}^{n} y_{i} x_{i}^{k}$

Retta di regressione M = 1

[[#Polinomio Algebrico ai minimi quadrati]] di grado 1
$r (x) = a_{0} + a_{1} x$
si ha
$\begin{aligned} H Γ & = B \\ [\begin{array}{c} h_{00} & h_{01} \\ h_{10} & h_{11} \end{array}] [\begin{array}{c} a_{0} \\ a_{1} \end{array}] & = [\begin{array}{c} b_{0} \\ b_{1} \end{array}] \\ [\begin{array}{c} s_{0} & s_{1} \\ s_{1} & s_{2} \end{array}] [\begin{array}{c} a_{0} \\ a_{1} \end{array}] & = [\begin{array}{c} b_{0} \\ b_{1} \end{array}] \end{aligned}$

dove
$\begin{aligned} a_{0} & = \frac{b_{0} s_{2} - b_{1} s_{1}}{s_{0} s_{2} - s_{1}^{2}} \\ a_{1} & = \frac{b_{1} s_{0} - b_{0} s_{1}}{s_{0} s_{2} - s_{1}^{2}} \end{aligned}$

metodo

Retta di regressione:

r (x) = a_{0} + a_{1} x

Elementi matrice $H$ :

h_{j k} = \sum_{i = 0}^{n} ψ_{j} (x_{i}) ψ_{k} (x_{i}) = \sum_{i = 0}^{n} x_{i}^{j} x_{i}^{k} = \sum_{i = 0}^{n} x_{i}^{j + k} \overset{△}{=} s_{j + k}

Termine noto $B$ :

b_{k} = \sum_{i = 0}^{n} y_{i} ψ_{k} (x_{i}) = \sum_{i = 0}^{n} y_{i} x_{i}^{k}

Coefficienti:

\begin{aligned} a_{0} & = \frac{b_{0} s_{2} - b_{1} s_{1}}{s_{0} s_{2} - s_{1}^{2}} \\ a_{1} & = \frac{b_{1} s_{0} - b_{0} s_{1}}{s_{0} s_{2} - s_{1}^{2}} \end{aligned}

Costruire la retta di regressione per le seguenti misurazioni:

$i$	0	1	2	3	4	5	6
$x_{i}$	2	3	4	5	6	8	10
$F_{i}$	7.0	8.3	9.4	11.3	12.3	14.4	15.9

F (x) = k (x - l) = k x - k l

In questo caso $a_{1} = k$
$n = 7$
Calcolo

\begin{aligned} s_{0} & = \sum_{i = 0}^{n} x_{i}^{0} = 7 \\ s_{1} & = \sum_{i = 0}^{n} x_{i}^{1 + 0} = 2 + 3 + 4 + 5 + 6 + 8 + 10 = 38 \\ s_{2} & = \sum_{i = 0}^{n} x_{i}^{2 + 0} = 4 + 9 + 16 + 25 + 36 + 64 + 100 = 254 \end{aligned}

per cui:

H = [\begin{matrix} 7 & 38 \\ 38 & 254 \end{matrix}]

Calcolo il termine noto:

\begin{aligned} b_{0} & = \sum_{i = 0}^{n} y_{i} x_{i}^{0} = 7.0 \cdot 2^{0} + \dots + 15.9 = 78.60 \\ b_{1} & = \sum_{i = 0}^{n} y_{i} x_{i}^{1} = 7.0 \cdot 2 + \dots + 15.9 \cdot 10 = 481 \end{aligned}

Calcolo i parametri

\begin{aligned} a_{0} & = \frac{78.6 \cdot 7 - 481 \cdot 38}{7 \cdot 38 - 38^{2}} & \approx 5.049 = - k l \\ a_{1} & = \dots & \approx 1.1383 = k \end{aligned}

type: line
labels: [2,3,4,5,6,8,10]
series:
  - title: Forza
    data: [7.0,8.3,9.4,11.3,12.3,14.4,15.9]
tension: 0.2
width: 80%
labelColors: false
fill: false
beginAtZero: false
bestFit: false
bestFitTitle: Retta di regressione
bestFitNumber: 0

Approssimazione trigonometrica

Ha periodo $T = 2 π$

Nodi: ${x_{i}, y_{i}} 0 \leq i \leq n$
Passo: $\frac{2 π}{n + 1}$

La funzione approssimante è una funzione del tipo:

T_{M} (x) = \frac{a_{0}}{2} + \sum_{k + 1}^{M} (a_{k} \cos (k x) + b_{k} \sin (k x))

Dobbiamo determinare i coefficienti $a_{k}, b_{k}$ : $2 M + 1$ coefficienti incogniti.

metodo

Funzione approssimante:
$T_{M} (x) = \frac{a_{0}}{2} + \sum_{k + 1}^{M} (a_{k} \cos (k x) + b_{k} \sin (k x))$

Coefficienti:
$\begin{aligned} a_{0} & = \frac{2}{n + 1} \sum_{i = 0}^{n} y_{i} \\ a_{k} & = \frac{2}{n + 1} \sum_{i = 0}^{n} y_{i} \cos (k x_{i}) 1 \leq k \leq M \\ b_{k} & = \frac{2}{n + 1} \sum_{i = 0}^{n} y_{i} \sin (k x_{i}) 1 \leq k \leq M \end{aligned}$

Interpolazione

interpolazione

Un tipo di approssimazione tale che la funzione approssimante $f_{n}$ rispetta la proprietà:
$f_{n} (x_{i}) = f_{i}$
dove $f_{i}$ sono i valori disponibili ed assunti da una funzione $f$ nei nodi $x_{i}$

Interpolazione polinomiale

Siano assegnati i valori ${f_{i}}$ che una funzione $f$ , di una variabile reale $x$ , assume in $n + 1$ nodi distinti ${x_{i}}, i = .0, 1, . . ., n$ .
Il problema dell'interpolazione polinomiale consiste nella determinazione di un polinomio di grado minimo che passi per i punti $P_{i} (x_{i}, f_{i}), i = 0, 1, . . ., n$ . Essondo i punti $n + 1$ , è sufficiente un polinomio di grado $n$ : $p_{n} \in P_{n}$ che risulti:

p_{n} (x_{i}) = f_{i} i = 0, 1, . . ., n

Si ha che il generico polinomio di grado $n$ è

p_{n} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n}

Per la determinazione dei coefficienti ci si riduce al sistema:

{\begin{cases} a_{0} + a_{1} x_{0} + a_{2} x_{0}^{2} + \dots + a_{n} x_{0}^{n} & = f_{0} \\ a_{0} + a_{1} x_{1} + a_{2} x_{1}^{2} + \dots + a_{n} x_{1}^{n} & = f_{1} \\ ⋮ \\ a_{0} + a_{1} x_{n} + a_{2} x_{n}^{2} + \dots + a_{n} x_{n}^{n} & = f_{n} \end{cases}

dal quale otteniamo la matrice dei coefficienti (di questo sistema), detta matrice di Vandermonde:

V = [\begin{matrix} 1 & x_{0} & x_{0}^{2} & \dots & x_{0}^{n} \\ 1 & x_{1} & x_{1}^{2} & \dots & x_{1}^{n} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & x_{n} & x_{n}^{2} & \dots & x_{n}^{n} \end{matrix}]

Questa matrice, nella base dei monomi, può risultare mal condizionata. Si preferisce quindi usare una forma diversa del polinomio, i [[#Polinomi di base di Lagrange]].

Polinomi di base di Lagrange

Si tratta di $n + 1$ polinomi di grado $n$ che chiameremo ${l_{i} (x)}$ :

l_{0} (x), l_{1} (x), . . ., l_{n} (x) \in P_{n}

ognuno dei quali soddisfa la seguente proprietà:

l_{k} (x_{i}) = δ_{k i} = {\begin{cases} 1, & i = k \\ 0, & i \neq k \end{cases}

Per cui:

l_{k} (x) = \prod_{i = 0, i \neq k}^{n} \frac{x - x_{i}}{x_{k} - x_{i}}

Si può a questo punto scrivere il polinomio interpolatore come:

p_{n} (x) = f_{0} l_{0} (x) + f_{1} l_{1} (x) + \dots + f_{n} l_{n} (x)

In breve:

metodo

Costruisco i polinomi di Lagrange:
$l_{k} (x) = \prod_{i = 0, i \neq k}^{n} \frac{x - x_{i}}{x_{k} - x_{i}}$
Scrivo il polinomio interpolatore come:
$p_{n} (x) = f_{0} l_{0} (x) + f_{1} l_{1} (x) + \dots + f_{n} l_{n} (x)$

esempio

❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗

Errore di interpolazione

Nell'interpolazione ci sono 2 sorgenti di errore:

[[#Errore di troncamento (interpolazione)]]: quello dovuto alla sostituzione della funzione con un polinomio
[[#Errore di propagazione (interpolazione)]]: quello dovuto a un errore nei dati

Definito $p_{n}^{⋆}$ il polinomio interpolatore ideale calcolato in corrispondenza ai valori esenti da errori.

p_{n}^{⋆} = f (x_{0}) l_{0} (x) + f (x_{1}) l_{1} (x) + \dots + f (x_{n}) l_{n} (x)

e $p_{n}$ il polinomio interpolatore trovato:

p_{n} (x) = f_{0} l_{0} (x) + f_{1} l_{1} (x) + \dots + f_{n} l_{n} (x)

definiamo l'errore di interpolazione come segue:

errore di interpolazione ($e_{int}(x)$)

$\begin{aligned} E_{i n t} (x) & = f_{x} - p_{n} (x) = \\ = \underset{E_{n} (x)}{\underset{⏟}{f (x) - p_{n}^{⋆} (x)}} + \underset{E_{n}^{⋆} (x)}{\underset{⏟}{p_{n}^{⋆} (x) - p_{n} (x)}} \\ = E_{n} (x) + E_{n}^{⋆} (x) \end{aligned}$
dove

$E_{n} (x) =$ Errore di troncamento
$E_{n}^{⋆} (x) =$ Errore di propagazione

Per cui è ovvio che, dalla [[##disuguaglianza triangolare]]

maggiorazione errore totale

$| E_{n}^{T O T} (x) | \leq | E_{n}^{⋆} (x) | + | E_{n} (x) |$

Errore di troncamento (interpolazione)

E_{n} (x) = Π_{n} (x) \cdot \frac{f^{(n + 1)} (ξ (x))}{(n + 1)!} ξ (x) \in [x_{0}, x_{}]

con $Π_{n} (x)$ polinomio nodale

Π_{n} (x) = \prod_{i = 0}^{n} (x - x_{i})

Dell'errore di troncamento, possiamo dare la seguente maggiorazione:

errore di propagazione

$| E_{n} (x) | \leq | Π_{n} (x) | max_{x_{0}, x_{n}} \frac{| f^{(n + 1)} (x) |}{(n + 1)!}$

Errore di propagazione (interpolazione)

errore di propagazione

$| E_{n}^{⋆} (x) | \leq ε \sum_{i = 0}^{n} | l_{i} (x) | = ε Λ (x)$
dove

$ε =$ l'errore sui dati
$l_{i} (x) =$ è l' $i$ -esimo polinomio in base di Lagrange
$Λ (x) =$ è la funzione di Lebesgue
ricordo:
$l_{i} (x) = \prod_{\begin{array}{r} j = 0 \\ i \neq j \end{array}}^{n} \frac{x - x_{j}}{x_{i} - x_{j}}$

Interpolazione trigonometrica

metodo

Nodi: ${x_{i}, y_{i}} 0 \leq i \leq n$
$x_{i} = i \frac{2 π}{n + 1}$

Polinomio interpolatore trigonometrico
$T_{n} (x) = \frac{a_{0}}{2} + \sum_{k = 0}^{\frac{n}{2}} (a_{k} \cos (k x) + b_{k} \sin (k x))$
Coefficienti:
$\begin{array}{r} a_{k} = \frac{2}{n + 1} \sum_{i = 0}^{n} y_{i} \cos (k x_{i}) 0 \leq k \leq \frac{n}{2} \\ b_{k} = \frac{2}{n + 1} \sum_{i = 0}^{n} y_{i} \sin (k x_{i}) 1 \leq k \leq \frac{n}{2} \end{array}$

Interpolazione Spline

Partizione

partizione ($\delta$)

La partizione $Δ$ di un intervallo $[a, b]$ è un insieme di punti tali che
$Δ : a = x_{0} < x_{1} < \dots < x_{n - 1} < x_{n} = b$

Funzione Spline

funzione spline

La funzione Spline di grado $m$ associata alla partizione $Δ$ è $S_{m} (x)$ dove

$S_{m} (x)$ è un polinomio di grado $m$ nei sotto-intervalli $[x_{i - 1}, x_{i}], 1 \leq i \leq n$
$S_{m} (x) \in C^{m - 1} [a, b] ⟺ S_{m}^{(k)} (x_{i}^{-}) = S_{m}^{(k)} (x_{i}^{+}) \forall 1 \leq k \leq m - 1$

Spline lineare

$S_{1} (x)$ è un polinomio di grado 1 nei sottointervalli $T_{i} = [x_{i - 1}, x_{i}] 1 \leq i \leq n$ tale che

S_{1} (x_{i}^{-}) = S_{1} (x_{i}^{+})

Nodi: ${x_{i}, y_{i}} 0 \leq i \leq n$
La spline lineare interpolante è un polinomio a tratti continuo che soddisfa le condizioni di interpolazione

S_{1} (x_{i}) = y_{i}

metodo

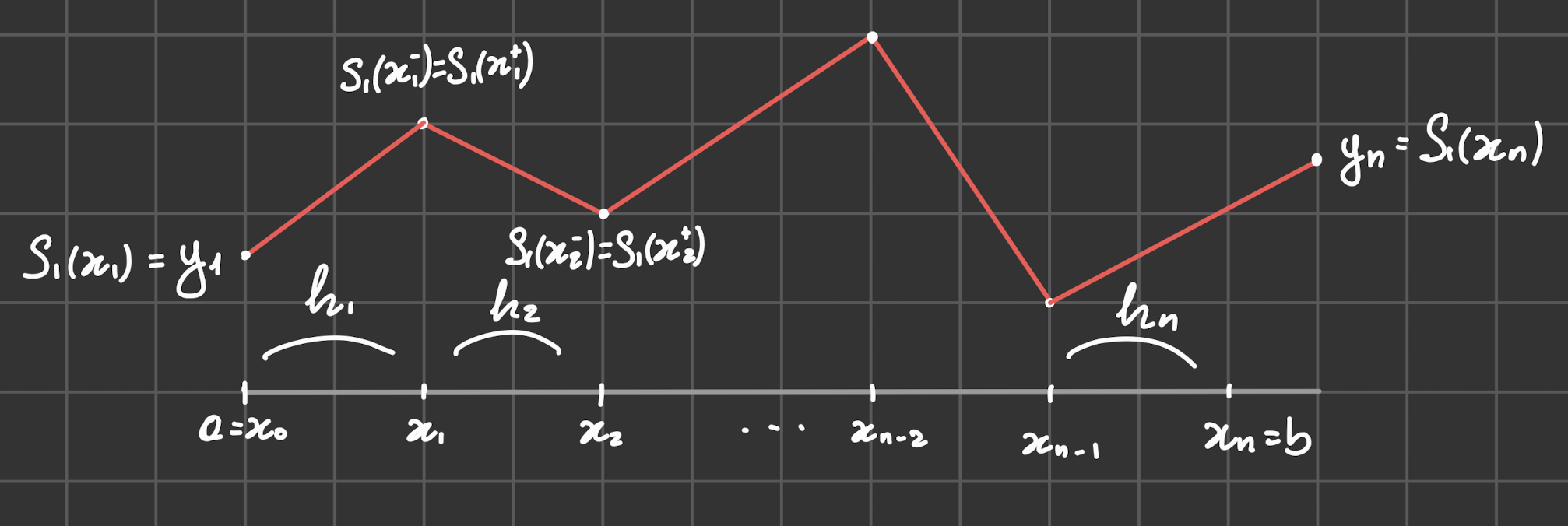
Spline lineare interpolante, $x \in [x_{i - 1}, x_{i}]$
$S_{1} (x) \frac{1}{h_{i}} ((x_{i} - x) y_{i - 1} + (x - x_{i - 1}) y_{i})$

Base lagrangiana:
$B_{l} (x) = {\begin{cases} \frac{1}{h_{l}} (x - x_{l - 1}), x_{l - 1} \leq x \leq x_{l} \\ \frac{1}{h_{l}} (x_{l + 1} - x_{l}), x_{l} \leq x \leq x_{l + 1} \\ 0, Altrove \end{cases}$
Per cui la spline lineare interpolante in base lagrangiana diventa:
$S_{1} (x) = \sum_{i = 0}^{n} y_{i} B_{i} (x)$