05.1 Metodo di Eulero

Metodo di Eulero

Introduzione del metodo

☑️ Ipotesi

ipotesi

Algoritmo

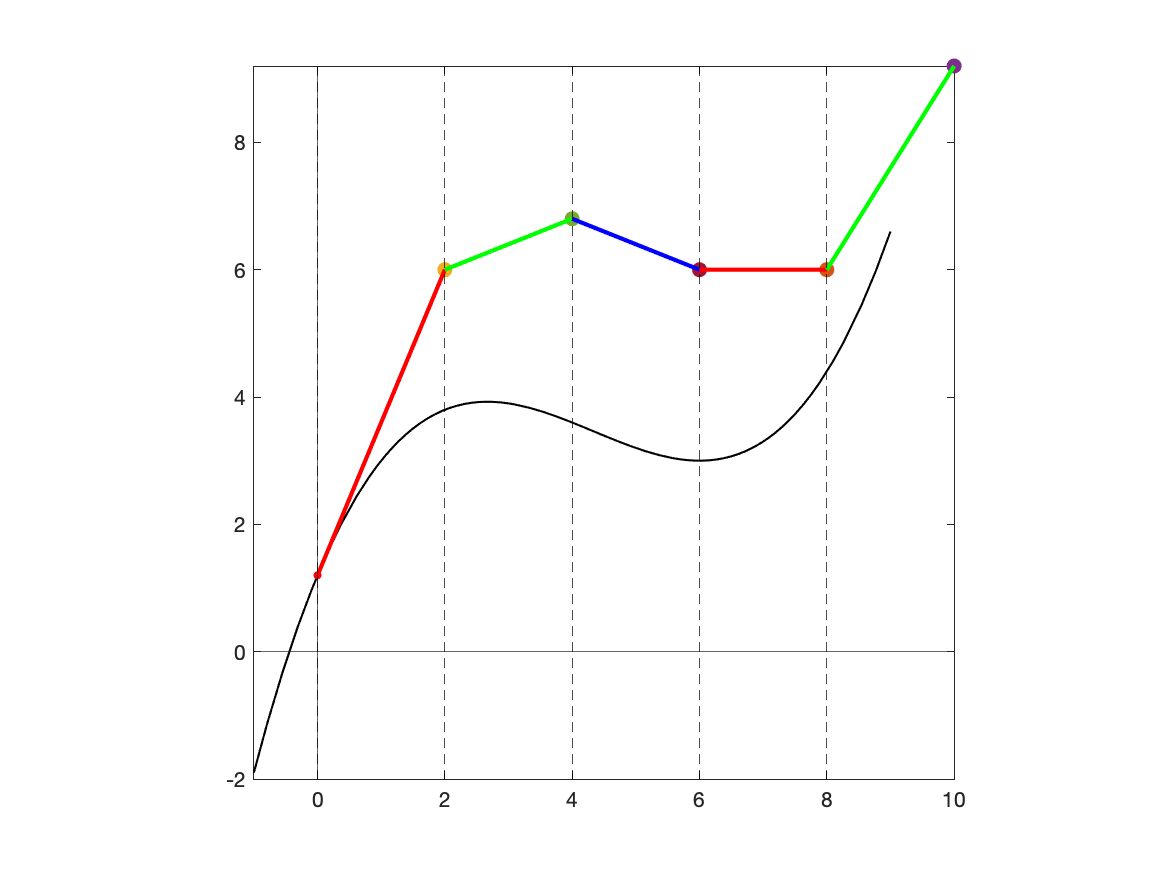
Discretizzazione

$I = [x_{0}, x_{0} + β]$ intervallo di discretizzazione.

Nodi: $t_{i} = t_{0} + i h 1 \leq i \leq n y_{0} = y (t_{0})$
Approssimazioni: $y_{i} = y (t_{i})$

Scrivo $y (t)$ come:

y (t) = y (t_{0}) + (t - t_{0}) y^{'} (t_{0}) + \frac{(t - t_{0})^{2}}{2} y^{″} (τ_{0}) con τ_{0} \in [t_{0}, t_{1}], t_{1} = t_{0} + h

Calcolato in $t_{1}$ diventa

y (t_{1}) = y (t_{0}) + (t_{1} - t_{0}) y^{'} (t_{0}) + . . . + R (t_{1}, h, y)

Dove $R (t_{1}, h, y)$ è l'#Errore di troncamento locale.
Essendo, per come è stato definito il problema

\begin{aligned} t_{1} - t_{0} & = h \\ y^{'} (t_{0}) & = f (t_{0}, y (t_{0})) \end{aligned}

posso scrivere:

y (t_{1}) = y (t_{0}) + h f (t_{0}, y (t_{0})) + R (t_{1}, h, y)

E posso quindi scrivere l'approssimazione $y_{1}$ come

y_{1} = y_{0} + h f (t_{0}, y_{0})

algoritmo

${\begin{cases} y_{i + 1} & = y_{i} + h f (t_{i}, y_{i}) \\ y_{0} & = y (t_{0}) \end{cases}$

Errori

Errore di Troncamento Globale

errore di troncamento globale

$e_{i} = y (t_{i}) - y_{i}$

Errore di troncamento locale

errore di troncamento locale metodo di eulero

$R (t_{i}, h, y) = \frac{h^{2}}{2} y^{″} (τ_{i}) τ_{i} \in [t_{i}, t_{i + 1}]$

Convergenza

Condizioni di convergenza

NON VISTO

Ordine di convergenza

ordine di convergenza

Il [[#Metodo di Eulero]] ha ordine di convergenza pari a 1:
$p = 1$

Stima iterazioni necessarie

NON VISTO

Criterio di arresto

Criterio di arresto a posteriori

Posso interrompere l'algoritmo quando l'errore al passo k è minore di una tolleranza scelta $ε$ .

| e_{k} | \leq ε

Implementazione in Matlab

Riportare la function per l'applicazione del metodo in matlab

function [Ti,Yi] = MetodoEulero(fun, I, y0, n_step)

% Metodo di Eulero

% Calcola la soluzione di una EDO del orimo ordine ai valori iniziali con

% il metodo di Eulero

% Input:

% fun(t,y): termine noto del problema (function)

% I(1:2): Estremi dell'intervallo di integrazione (vettore)

% y0(1): Condizione iniziale

% n_step: Numero passi temporali (scalare)

%

% Output:

% Ti(1:n_step + 1): Nodi di discretizzazione (vettore)

% Yi(1:n_step + 1): Vettore delle approssimazioni (vettore)

t0 = I(1);

tf = I(2);

% Passo di discretizzazione

h = (tf-t0)/n_step;

% Griglia dei nodi: equispaziata

Ti = linspace(t0,tf, n_step + 1);

Ti = Ti'; % Rendo Ti un vettore colonna

% Inizializzazioni

Yi = nan(n_step + 1, 1);

Yi(1) = y0;

% Metodo di Eulero

for i= 1:n_step

Yi(i+1) = Yi(i) + h*fun(Ti(i), Yi(i));

end

end