03.3 Il metodo delle Secanti

3.3 Metodo delle Secanti

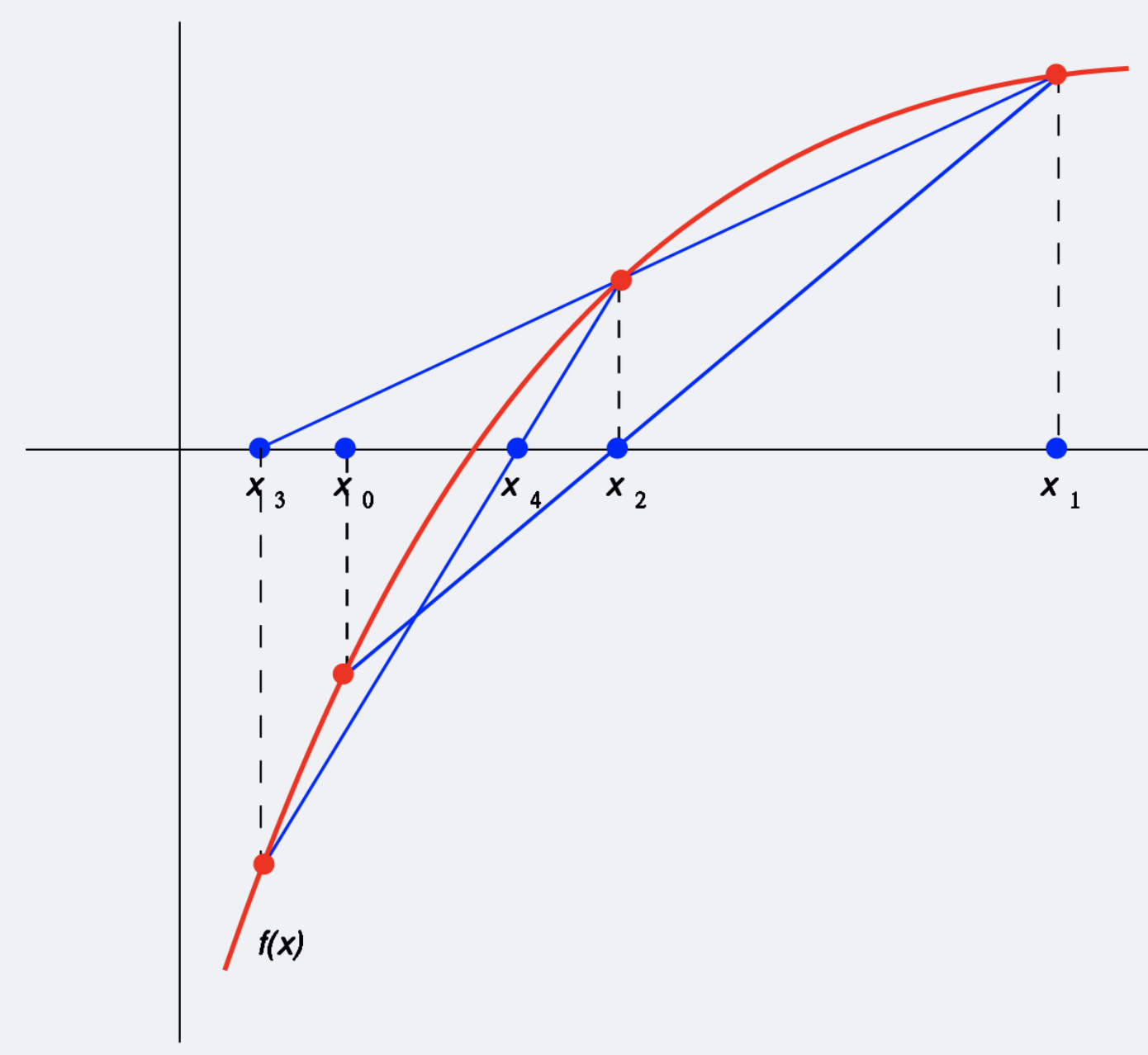
Il metodo delle Secanti consiste nell'approssimare localmente la funzione con la retta secante passante per i due estremi dell'intervallo I.

Schermata 2024-10-23 alle 13.46.49.png

☑️ Ipotesi

ipotesi
  1. f(x)∈C(I=[a,b])
  2. f′(xk)≠0∀k
  3. f′(x)≠0x∈I allora il metodo converge per x0,x1∈J⊂I
  4. f″(x)≠0x∈I allora il metodo converge

Algoritmo

Scelgo 2 approssimazioni iniziali: x0,x1
Poi, per k=2,3,... calcolo la soluzione approssimata come radice della retta secante passante per x0 e x1:

xk=xk−1−f(xk−1)xk−1−xk−2f(xk−1)−f(xk−2)
algoritmo

{x0,x1Approssimazioni inizialixk=xk−1−f(xk−1)xk−1−xk−2f(xk−1)−f(xk−2)

Convergenza

prop - cs di convergenza per secanti

Se:

  • I=[a,b] intervallo di separazione, simmetrico intorno la radice ξ
  • f,f′,f″∈C2[a,b]
  • f′(x)≠0 per x∈[a,b]

Allora esiste un intorno J⊆I di ξ tale che, se x0,x1∈J, la successione delle approssimazioni {xk} converge a ξ con convergenza superlineare, cioè 1<p<2.

In particolare, se f″(x)≠0 in I, l'[[#Ordine di convergenza]] è
p=1+52

Ordine di convergenza

L'ordine di convergenza del metodo delle secanti è

p=1+52≈1.62

Essendo maggiore di 1 ma minore di 2 si dice che ha ordine di convergenza sopralineare.

Implementazione in Matlab

function [xk,errk, iter] = secanti_tol(x0,x1, f, N_max, tol)
% Input: (x0, x1, f, N_max, tol)
% x0, x1: Approx iniziali
%   f: Funzione di cui trovare gli zeri
%   N_max: Numero di iterazioni
%   tol: Tolleranza richiesta
%
% Output:
%   xk: approx dello zero
%   errk: Errore alla k-esima iterata
%   iter: Numero di iterazioni effettuate

errk  = tol + 1;
iter = 0;

while (iter < N_max) && (errk > tol)
    xk = x1 - f(x1)* (x1-x0) / (f(x1) - f(x0));
    errk = abs(xk-x1);
    x0 = x1;
    x1 = xk;
    iter = iter + 1;
end

fprintf('xk = %f', xk)
end