03.2 Il metodo delle Tangenti

3.2 Il metodo delle Tangenti

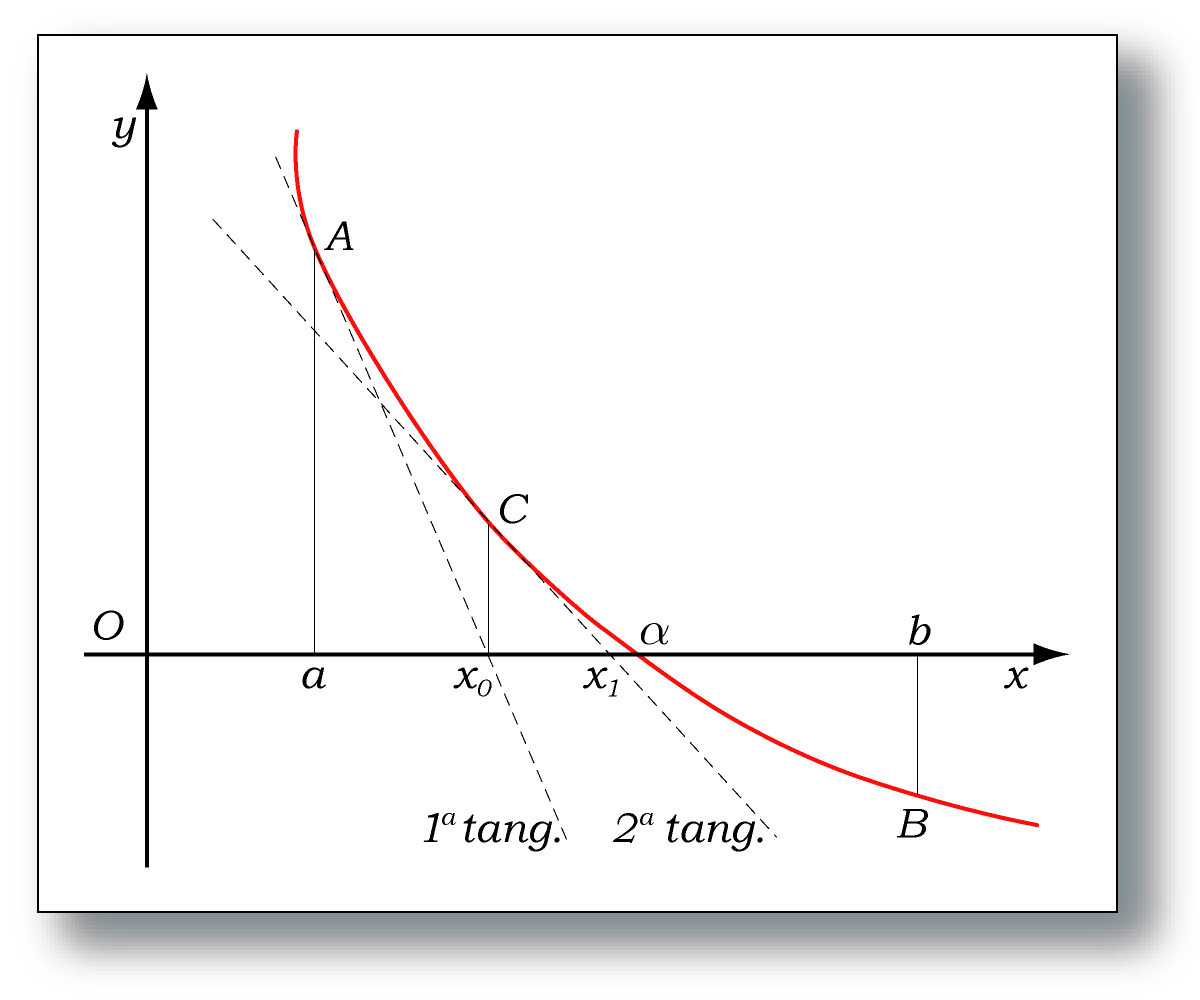
Il metodo delle tangenti, detto anche metodo di Newton sfrutta il Polinomio di Taylor per approssimare il valore delle funzioni. In questo caso è necessario scegliere un'approssimazione iniziale $x_{0}$ .

Si tratta di fatto di un metodo di linearizzazione. Infatti, come vedremo, interromperemo il Polinomio di Taylor al primo ordine, confondendo quindi il valore della funzione con il valore della tangente.

☑️ Ipotesi

Per l'applicabilità del metodo di newton, la funzione deve rispettare le seguenti ipotesi:

ipotesi

$I$ è Intervallo di separazione
$f (x) \in C^{1} (I = [a, b])$
$f^{'} (x) \neq 0 \forall k$

Algoritmo

Scelgo un'approssimazione iniziale $x_{0}$ .

Approssimo la funzione $f (x)$ con un polinomio di Taylor al secondo ordine:

f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + \frac{1}{2} f^{″} (τ) (x - x_{0})^{2} con τ \in [x_{0}, x]

Se cerco la radice di $f (x)$ impongo la funzione approssimata uguale a 0:

f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) \overset{!}{=} 0

da cui

x_{1} = x_{0} - \frac{f (x_{0})}{f^{'} (x_{0})}

motivo per cui dobbiamo imporre anche $f^{'} (x_{k}) \neq 0$ tra le #☑️ Ipotesi.

Dopodiché approssimo nuovamente la funzione con Taylor usando stavolta $x_{1}$ al posto di $x_{0}$ :

f (x) = f (x_{1}) + f^{'} (x_{1}) (x - x_{1}) \overset{!}{=} 0

da cui

x_{2} = x_{1} - \frac{f (x_{1})}{f^{'} (x_{1})}

Continuo ad iterare questo procedimento. Avrò così, in definitiva:

x_{k} = x_{k - 1} - \frac{f (x_{k - 1})}{f^{'} (x_{k - 1})}

Il metodo convergerà per alcuni valori di $x_{0} \in J \subset I$ (Ossia scegliendo $x_{0}$ abbastanza vicino a $ξ$ ).

algoritmo

${\begin{cases} x_{0} Punto iniziale \\ x_{k} = x_{k - 1} - \frac{f (x_{k - 1})}{f^{'} (x_{k - 1})} \end{cases}$

Convergenza

condizione necessaria di convergenza

Sia $I = [a, b]$ un intervallo di separazione di uno zero di $f$ ;

Sia:

$f \in C^{2} [a, b]$
$f^{'} (x) \neq 0$
$x \in [a, b]$

Allora esiste un intorno $J$ di $ξ$ , con $J \subset I$ , tale che, se $x_{0} \in J$ , la successione risulta convergente a $ξ$ .

Inoltre, se $f \in C^{3} [a, b]$ l'ordine di convergenza è $\geq 2$ .

convergenza con estremo di fourier

Sia:

$f \in C^{2} [a, b]$
$f (a) \cdot f (b) < 0$
$f^{″} (x) \neq 0$

per $x \in [a, b]$ , sia $x_{0}$ l'[[#Estremo di Fourier]] di $[a, b]$ , allora:

Esiste un unico $ξ \in (a, b)$ , tale che $f (ξ) = 0$
La successione ${φ (x_{n})}$ è monotona e converge a $ξ$
Se $f \in C^{3} [a, b]$ , la convergenza è quadratica

Estremo di Fourier

Se $f^{″} (x) \neq 0 \forall x \in I$ si può dimostrare che si può scegliere uno dei due estremi di $I$ come approssimazione iniziale $x_{0}$ .

Supponiamo di avere una funzione monotona, senza massimi o minimi locali, a concavità fissa.
L'estremo di Fourier di un intervallo è quello dei due tale che il prodotto $f (a) \cdot f^{″} (a) > 0$ dove $a$ è l'estremo.

Ordine di convergenza

ordine di convergenza per tangenti

$p = 2$

Per calcolare l'ordine di convergenza devo calcolare il limite:

lim_{k \to \infty} \frac{| e_{k + 1} |}{| e_{k} |^{p}} = C > 0 p \geq 1

Calcolo $| e_{k + 1} |$ :

| e_{k + 1} | = ξ - x_{k + 1} = (ξ - \frac{f (ξ)}{f^{'} (ξ)}) - x_{k + 1}

essendo $\frac{f (ξ)}{f^{'} (ξ)} = 0$ perché $f (ξ) = 0$ .

\begin{aligned} | e_{k + 1} | = ξ - x_{k + 1} & = (ξ - \frac{f (ξ)}{f^{'} (ξ)}) - x_{k + 1} = \\ = (ξ - \frac{f (ξ)}{f^{'} (ξ)}) - (x_{k} - \frac{f (x_{k})}{f^{'} (x_{k})}) = \\ = (ξ - x_{k}) - (\frac{f (ξ)}{f^{'} (ξ)} - \frac{f (x_{k})}{f^{'} (x_{k})}) = \end{aligned}

Sviluppando $f (x_{k})$ e $f^{'} (x_{k})$ in serie di Taylor e ricordando $ξ - x_{k} = e_{k}$ ottengo:

\begin{aligned} | e_{k + 1} | & = | e_{k} - (\frac{f (ξ)}{f^{'} (ξ)} - \frac{f (ξ) + f^{'} (ξ) (- e_{k}) + \frac{1}{2} f^{″} (ξ) e_{k}^{2}}{f^{'} (ξ)}) | \\ = \frac{1}{2} | \frac{f^{″} (ξ)}{f^{'} (ξ)} | | e_{k}^{2} | \end{aligned}

Si ha quindi che

\frac{| e_{k + 1} |}{| e_{k} |^{p}} \overset{p = 2}{\approx} \frac{1}{2} | \frac{f^{″} (ξ)}{f^{'} (ξ)} |

quindi

lim_{k \to \infty} \frac{| e_{k + 1} |}{| e_{k} |^{2}} = \frac{1}{2} | \frac{f^{″} (ξ)}{f^{'} (ξ)} |

Allora l'ordine di convergenza del metodo delle tangenti è $p = 2$ .

Implementazione in Matlab

function xk = tangenti(x0,f, df, N_max)

% Input:
%   x0: approx iniziale
%   f, df: funzione e derivata
%   N_max: numero di iterazioni
% 
% Output:
%   xk: approx dello zero

for i = 1:N_max
    xk = x0 - f(x0) / df(x0);
    errk = abs(xk - x0);
    x0 = xk;
    fprintf('k = %3i x_k = %14.12f err=%9.3e f=%18.12f f''=%18.12f \n', i, xk, errk, f(x0), df(x0));
end

end

Metodo di Newton in $R^{n}$

Al link 03.4 Metodo di Newton in n dimensioni

Se in $R$ possiamo riscrivere una funzione sviluppandola in un Polinomio di Taylor, lo stesso possiamo fare con $R^{n}$ .

Sia $F (X) : R^{n} \to R^{n}$ , posso scrivere

F (X) = F (X^{(k)}) + J_{F} (X^{(k)}) (X - X^{(k)}) + . . .

dove

J_{F} (X) = [\begin{matrix} \frac{\partial f_{1}}{\partial x_{1}} & \frac{\partial f_{1}}{\partial x_{2}} & \dots & \frac{\partial f_{1}}{\partial x_{n}} \\ \frac{\partial f_{2}}{\partial x_{1}} & \frac{\partial f_{2}}{\partial x_{2}} & \dots & \frac{\partial f_{2}}{\partial x_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \frac{\partial f_{n}}{\partial x_{1}} & \frac{\partial f_{n}}{\partial x_{2}} & \dots & \frac{\partial f_{n}}{\partial x_{n}} \end{matrix}]