02. Richiami di algebra lineare
2. Richiami di Algebra Lineare
Generalità
Raggio Spettrale
Siano
Matrice inversa
- Calcolare il
- Assicurarsi che
- Calcolare la #matrice dei complementi algebrici
- Calcolare la matrice trasposta della matrice dei complementi algebrici
- Moltiplicare per
Matrice dei complementi algebrici
Data la matrice
i Cofattori
La matrice dei cofattori è la matrice:
Norma
Ci troviamo in uno spazio vettoriale.
Sia
Si definisce Norma Euclidea la seguente:
l'operatore con le seguenti proprietà:
--> Disuguaglianza triangolare
Esiste più di una norma.
Norma
Alcune norme notevoli sono per:
Norma di matrice
Sia
Viene detta norma di matrice una funzione
Vedremo tornare utili le cosiddette norme indotte da vettori
Norma indotta da vettore
Si definisce la norma di una matrice come segue:
con
Vale, per le norme indotte da vettori, la #Relazione di compatibilità:
Relazione di Compatibilità
Dati
Dimostrazione:
A partire dalla definizione di [[#Norma indotta da vettore]]:
Essendo
Da cui segue la relazione di compatibilità
c.v.d.
Principali norme indotte
La [[#Norma per righe]] e [[#Norma per colonne]] sono uguali se la matrice
Norma per colonne
Norma per righe
Norma spettrale
Dove
Contrazioni
Matrici "Speciali"
Matrici diagonalmente Dominanti
È data una matrice
Matrice Diagonalmente Dominante Righe
Ossia se ogni elemento sulla diagonale è maggiore (in modulo) della somma degli altri elementi della stessa riga.
Matrice Diagonalmente Dominante per Colonne
Ossia se ogni elemento sulla diagonale è maggiore (in modulo) della somma degli altri elementi della stessa colonna.
Matrice definita positiva
Una matrice
Una matrice definita positiva gode delle seguenti proprietà:
- Ha autovalori reali (poiché è simmetrica)
- Ha autovalori positivi
- Ha
è invertibile
Condizioni per matrici definite positive
Condizione Sufficiente per matrice definita positiva
Una matrice
- La posso riscrivere nella forma
- è diagonale dominante e
Dimostrazione
Dimostro il punto 2.
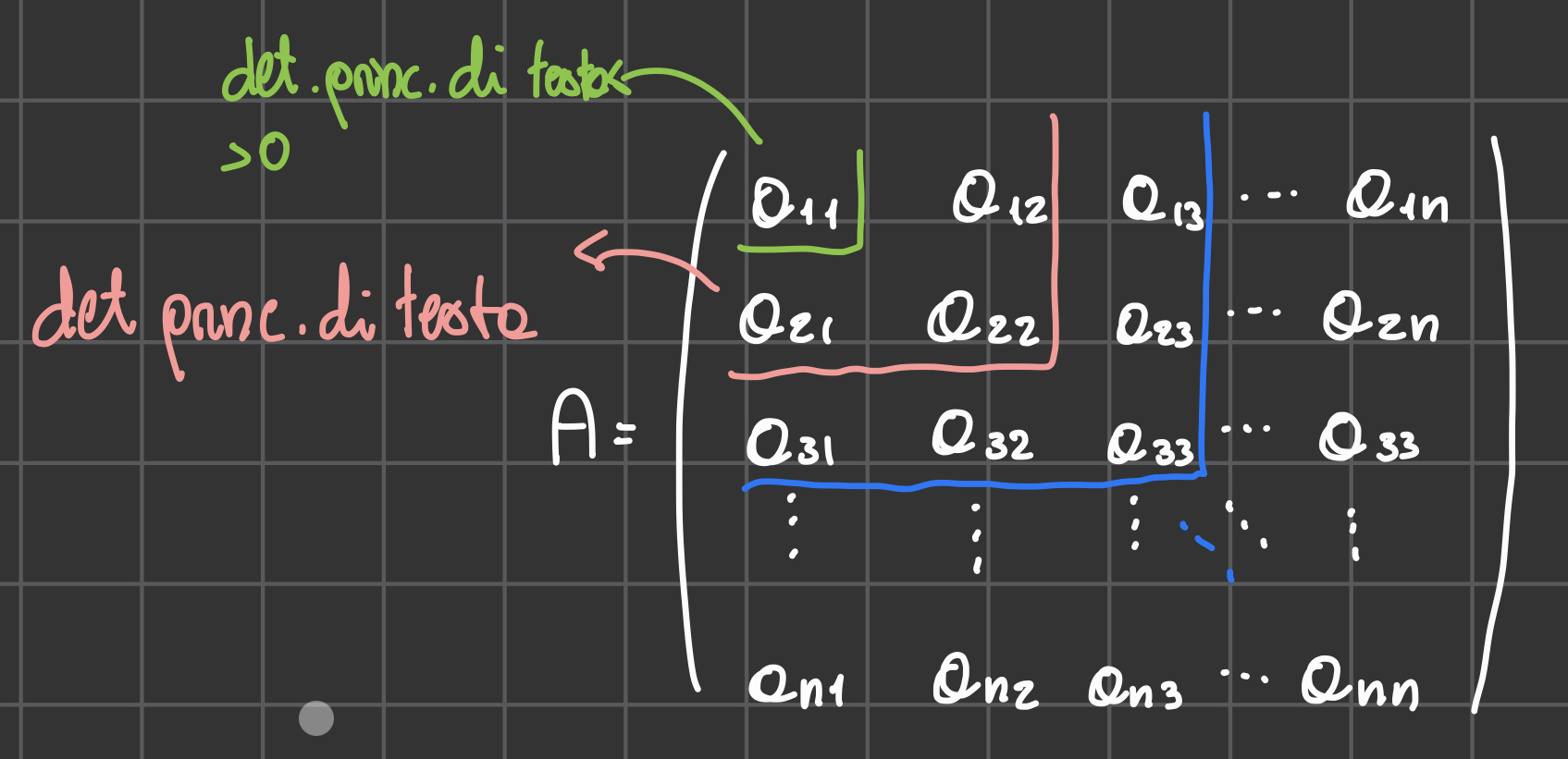
Condizione Necessaria e Sufficiente per matrice definita positiva
CNS affinché una matrice
Convergenza
Una matrice
Una matrice è convergente se e solo se