Nonlinear follow-the-leader models of traffic flow

Follow the leader theory of traffic

Single-lane dense traffic with no passing.

each driver reacts in some specific fashion to a stimulus from the car ahed of and/or behind them.

The theory applies mainly to dense traffic.

Basic idea:

response = sensitivity \cdot stimulus

response is taken as the acceleration of the vehicle as the driver has direct control over this parameter.
The stimulus is a function fo the position of cars and their time derivatives (speed)

It has been established that there is correlation between driver response and relative speed of their car and the one ahead. The stimulus is than taken as the relative speed.

Equations

{\ddot{x}}_{n + 1} (t + T) = λ [{\dot{x}}_{n} (t) - {\dot{x}}_{n + 1} (t)] (2)

$x_{n} :$ position of the $n^{t n}$ car
$T :$ reaction time
$λ :$ sensitivity

Possible sensitivity functions:

{\begin{cases} 1. constant & λ = a \\ 2. step function & λ = {\begin{cases} a, s \leq s^{*} \\ b, s > s^{*} \end{cases} \\ 3. reciprocal spacing & λ = \frac{c}{s} \end{cases}

where:

$s = x_{n} - x_{n + 1}$ (the spacing)
$a, b, c$ are constants

General equation:

λ = a \frac{{[{\dot{x}}_{n + 1} (t)]}^{m}}{[x_{n} (t) - x_{n + 1} (t)]^{l}}

This can lead to some specific forms for the sensitivity:

{\begin{cases} Edie: & λ = c \frac{{\dot{x}}_{n + 1}}{s^{2}} (6) \\ Leading to Greenshield: & λ = \frac{c}{s^{2}} (7) \end{cases}

For the validity of each model, we have to look at 2 things:

Stability - Only for the linear form (otherwise, too difficult)
- Same bounds are applied for the non linear cases
  - This is possible as long the nonlinear system only has small perturbations (?piccole oscillazioni?)
Steady-state flow characteristics

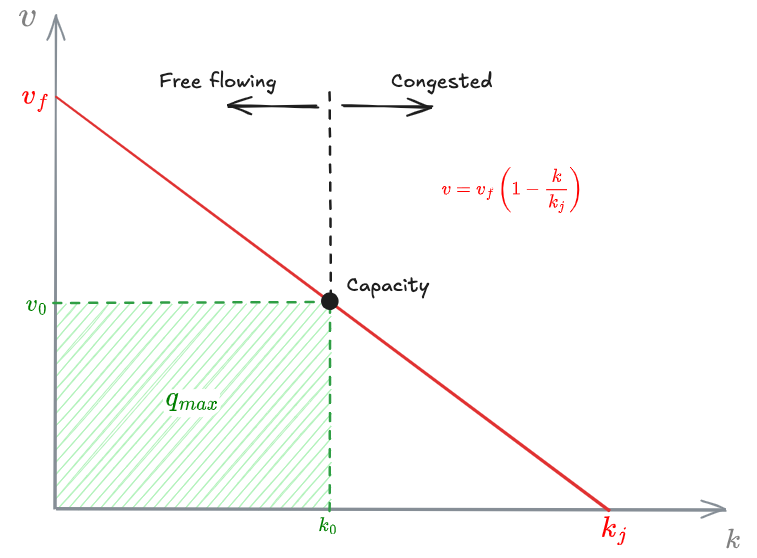
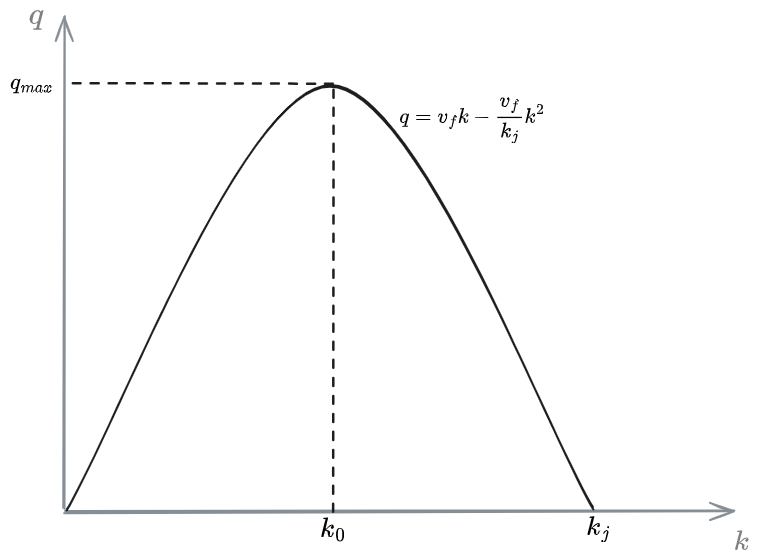
Steady flow characteristics

For steady-state flow characteristics is possible to obtain a fairly complete description corresponding to any sensitivity given by an equation such as the one used in the following:

{\ddot{x}}_{n + 1} (t + Δ t) = a \frac{[{\dot{x}}_{n + 1} (t)]^{m}}{[x_{n} (t) - x_{n + 1} (t)]^{l}} [{\dot{x}}_{n} (t) - {\dot{x}}_{n + 1} (t)] (9)

[?] Pag. 547/548. Why does integrating the equation yields the steady-state flow equation?

Greenshield k-v model

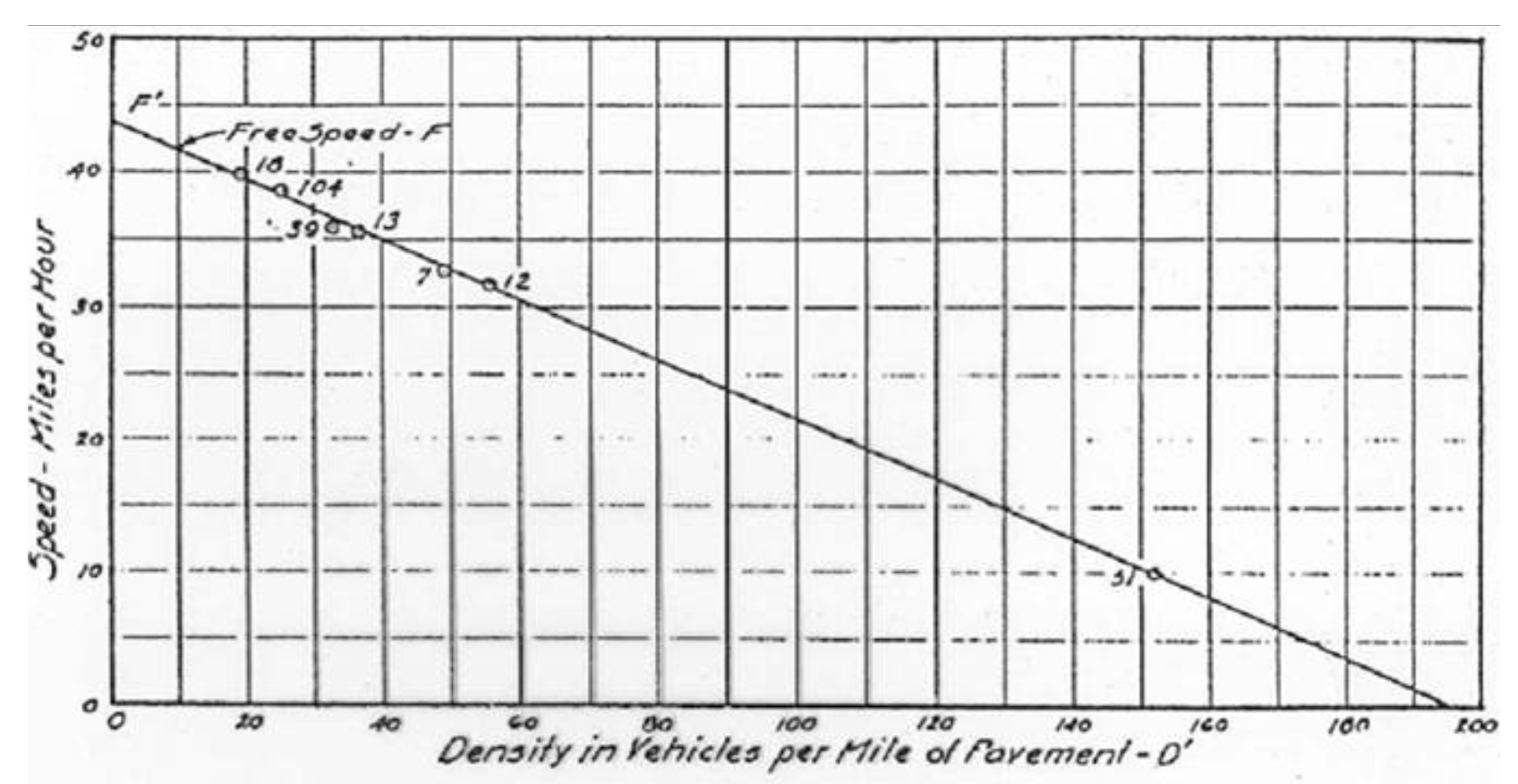
Schermata 2024-12-06 alle 17.14.15.png

The figure above shows the original Greenshield k-v model. He described the average speed as a function of density, requaring 2 calibration parameters

the greenshield $k-v$ model

Greenshield k-v model - 03 - Fundamentals of traffic flow modeling - OMT 2024-12-06 17.18.32.excalidraw.png

$v = v_{f} (1 - \frac{k}{k_{j}})$
where:

$v_{f} :$ Free flow speed - Speed at which vehicles travel when density is very low
$k_{j} :$ Jam density - Maximum density at the infrastructure when vehicles are in a gridlock jam, completely stopped

Given $q_{m a x}$ is the maximum flow of the infrastructure, the capacity, this is given by the area of the rectangle of sides $v_{0}$ and $k_{0}$ .

The capacity point also distinguishes between two states:

Congestion
Free flowing

finding $q_{max}$

$v_{0}$ and $k_{0}$ can be obtained as follows. According to the fundamental equation of traffic and to the Greenshield model
${\begin{cases} q = v k \\ v = v_{f} (1 - \frac{k}{k_{j}}) \end{cases}$
Combining the 2 equations:
$\begin{aligned} q & = v_{f} (1 - \frac{k}{k_{j}}) k = \\ = v_{f} k - \frac{v_{f}}{k_{j}} k^{2} \end{aligned}$
To find the maximum of this funciton, we can derive and impose equal to 0:
$\begin{aligned} \frac{\partial q}{\partial k} = \frac{\partial}{\partial k} (v_{f} k - \frac{v_{f}}{k_{j}} k^{2}) & \overset{!}{=} 0 \\ v_{f} - 2 \frac{v_{f}}{k_{j}} k & = 0 \\ k = \frac{1}{2} k_{j} \end{aligned}$
So,
$k_{0} = \frac{1}{2} k_{j} v_{0} = \frac{1}{2} v_{f}$

03 - Fundamentals of traffic flow modeling - OMT 2024-12-06 17.31.49.excalidraw.png

Experimental and observational data

2 types of data:

Phenomenological flow & Density measurements
- Tunnels of New York City area by the Port of New York Authority
  - No passing allowed
  - Fairly congested for long periods every day
Records of follow-the-leader experiments
- General Motors Technical Center test track
  - Used to obtain stimulus-response laws with constant sensitivity
- More tests in General Motors Technical Center test track
- Tunnels of New York
  - To compare macroscopic phenomenological measurements with microscopic results of follow-the-leader theory

Phenomenological flow & Density measurements

Tunnels of New York City area by the Port of New York Authority
- No passing allowed
- Fairly congested for long periods every day

Records of follow-the-leader experiments

General Motors Technical Center test track
- Used to obtain stimulus-response laws with constant sensitivity
More tests in General Motors Technical Center test track
Tunnels of New York
- To compare macroscopic phenomenological measurements with microscopic results of follow-the-leader theory

The data was used in 2 ways:

Phenomenological study of the time averages of space and speed
Timewise correlation study of the response of the following car with various functionals assumed for the product of stimulus times sensitivity

Experiment conducted with 2 cars.
Assumptions:

Headway and speed of the 2 cars are the same of the time and space averages of the whole stream of traffic
First equation (11)

y_{i} \overset{△}{=} f_{m} ({\overset{―}{u}}_{i}) = {\begin{cases} {\overset{―}{u}}_{i}^{1 - m} & m \neq 1 \\ \ln ({\overset{―}{u}}_{i}) & m = 1 \end{cases} x_{i} \overset{△}{=} f_{l} ({\overset{―}{s}}_{i}) = {\begin{cases} {\overset{―}{s}}_{i}^{1 - l} & l \neq 1 \\ \ln ({\overset{―}{s}}_{i}) & l = 1 \end{cases}

Linear correlation between $y_{i}$ and $x_{i}$ was evaluated. They computed the correlation coefficient for different values of $m$ and $l$ .

Also, they calculated the standard deviation for the coefficient $c$ of eq (11).

Difficulties:

Limited number of runs $i$ . Only 18
Drivers do not necessarily have the same coefficients $c$ and $c^{'}$

The objective was not to find non-integer values of $m$ and $l$ to maximize correlation. Rather to discover trends, like, are $m$ and $l$ likely to be positive or negative?

03 - Fundamentals of traffic flow modeling - OMT#Edie k-v model

Follow the leader experiments

Used data of 18 experiments in the Lincoln Tunnel of New York.

2 approaches:

Phenomenological aspects
Timewise correlation study