Standard Normal Distribution

The Standard Normal Distribution (or z distribution) is a particular case of the Normal distribution. The variable z is a normal distribution with mean 0 and variance 1:

z \sim N (0, 1)

The standard normal distribution is often used to estimate a Confidence Interval for statistics.

Probability Density Function

The Probability Density Function for the standard normal distribution is:

pdf for standard normal distribution

$f_{X} (x) = \frac{1}{\sqrt{2 π}} e^{\frac{x^{2}}{2}}$

Properties

symbol:: $N \sim (0, 1)$
mean:: 0
variance:: 1
kurtosis:: 0
skewness:: 1

Statistical tables

There are mainly 2 kind of statistical tables for the #Standard Normal Distribution.

Area from 0 to z

![[areas-under-the-standard-normal-curve-from-0-to-z.pdf]]

A use case of this table is to find Confidence Interval.

We need to estimate a statistic using the following degree of confidence (at which we associate a level of significance):

$D_{c} :$ degree of confidence
$α = 1 - D_{c} :$ level of significance

The table contains 3 values:

The first column contains the unit and the first decimal place of the value of z for any significance level
The first row contains the second decimal digit of the value of z
Each other cell contains the value of the area under the graph between 0 and z

The Degree of confidence refers to the area from $- z$ to $z$ . The tables give value for the area between $0$ and $z$ . So, we need to take the degree of confidence and divide it by 2.

Now we can look for this value in the table and read the corresponding value in the first column and first row and we will have found $z$ .

We want $α = 0.05$ . This means that we need a degree of confidence equal to 0.95 (95%). We need to look in the table for $\frac{0.95}{2} = 0.475$ .

For that value, we can see that in the first column we find 1.9 and in the first row we find 0.06.

This means that our value of $z$ is
$z = 1.96$

Area from - $\infty$ to z

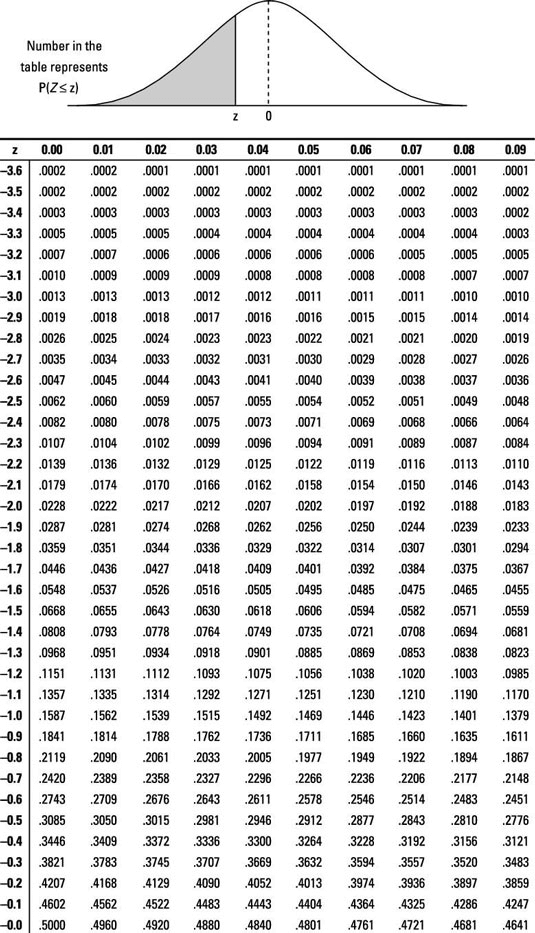
A use case of this table is to find Confidence Interval.

We need to estimate a statistic using the following degree of confidence (at which we associate a level of significance):

$D_{c} :$ degree of confidence
$α = 1 - D_{c} :$ level of significance

The table contains 3 values:

The first column contains the unit and the first decimal place of the value of z for any significance level
The first row contains the second decimal digit of the value of z
Each other cell contains the value of the area under the graph between $- \infty$ and z

The Degree of confidence refers to the area from $- z$ to $z$ . The tables give value for the area between $- \infty$ and $z$ . What we can read on the graph directly though is the Level of significance, $α$ . In fact, the area between $- \infty$ and $z$ is half the level of significance.

We look on the table for the cell containing the value $\frac{α}{2}$ then read the corresponding value of $z$ .

We want $α = 0.05$ . This means that we need a degree of confidence equal to 0.95 (95%). On the table we have to look for:
$\frac{α}{2} = \frac{0.05}{2} = 0.025$
Ignoring the sign for now, we can see from the table that the unit and first decimal digit of $z$ are 1.9 and the second decimal digit is 0.06. Therefore,
$z = 1.96$

Standard Normal Distribution

Probability Density Function

Properties

Statistical tables

Area from 0 to z

Area from -∞ to z

Area from - $\infty$ to z