Confidence Interval

A confidence interval is the interval in which a population statistic is contained when estimated by a sample statistic.

Let $μ$ be some population mean of same value and let $\overset{―}{X}$ be the mean of a sample of the population. Given an Level of significance of $α$ (s.t. the interval is accurate in $(1 - α) %$ of cases), then a Confidence Interval for the population mean is:

μ \in [\overset{―}{X} - z_{1 - \frac{α}{2}} \frac{σ}{\sqrt{n}}; \overset{―}{X} + z_{1 - \frac{α}{2}} \frac{σ}{\sqrt{n}}]

where $z_{1 - \frac{α}{2}}$ is the value of z (where z follows a Standard Normal Distribution) such that the area under the curve is equal to $1 - \frac{α}{2}$ .

Let's suppose $z$ is the value we are looking for (for example, the exact value of $μ$ ). Let $Z$ be any possible value of the Standard Normal Distribution. We can evaluate the probability:

P (Z \leq z)

as the area in the interval $(- \infty, z)$ . If for example we want that our estimate is accurate with a Degree of confidence of 95%, all we need to do is make sure we select a range wide enough such that, the range in question as an area of at least 0.95. That means, the area in the interval $(- \infty, z)$ has to be $\frac{0.05}{2}$ . (notice how the curve is symmetric and we want 95% to be the area in the middle). So, if we can find the value of $z$ such that the area under the curve is $0.025$ , we will have a range of values that ensures us that the estimate is accurate at 95%.

In order to find this value it's important to use statistic tables. For the Standard Normal Distribution you can read more about them in Standard Normal Distribution#Statistical tables.

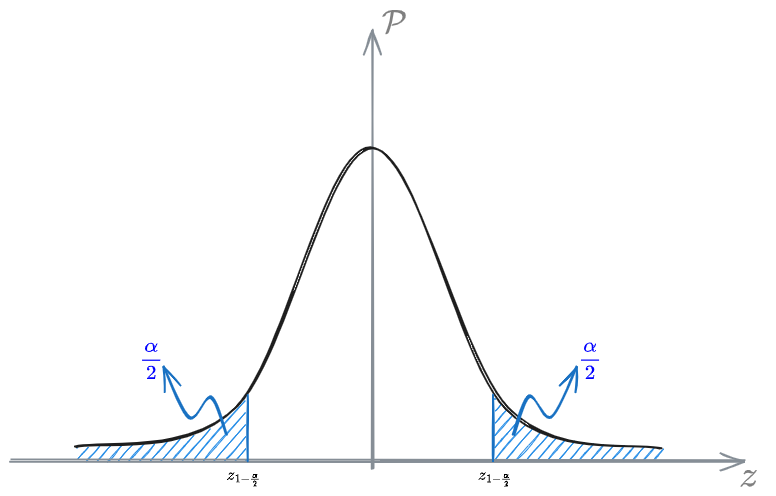
We use the Standard normal distribution since is well known. Then, we scale it according to a factor dependent on the variance of the variable we are interested in: $\frac{σ}{\sqrt{n}}$ .

One particular variable of a population has a mean of $μ$ (unknown). We have a sample of the population with a mean for the same variable equal to $\overset{―}{X}$ . Let's suppose we know the population variance, $σ^{2}$ . The sample is composed of $n$ elements.

We want an estimate for the population mean with 95% confidence. This mean we want an $α = 0.05$ .

We are basically looking for the value:
$z_{1 - \frac{α}{2}} = z_{1 - \frac{0.05}{2}} = z_{1 - 0.025} = z_{0.975}$
that is the value such that the area under the density distribution is equal to 0.975.

From the probability table we can find out that such value is:
$z = 1.960$
given a large number of observations.

$α :$ Level of significance
The percentage is the Degree of confidence

We are assuming to know the variance of the population. This is clearly impossible. Actually, also the variance, as the mean, follows a random probability distribution (that can be proven to be a ???). For the porpuses we are usually interested in, we can simply use the sample variance ( $s^{2}$ ) in place of the population variance.