02 - Fundamentals fo Queuing Theory - OMT

Queues appear when a flow of vehicles, persons or objects wants to receive a service that implies a restriction. Typically, services have a limited capacity or are offered only with some frequency, which may lead to queues, delays and waits.

The subject that studies queues is referred to Queuing Theory (see also 03. Variabili Aleatorie#Teoria delle code, 05. Teoria del Deflusso#Teoria delle code).

Most of the complexities of queuing theory come from the stochastic nature of the processes involved.

Components of a queuing system

Server: the restriction
Storage: where the costumer waits
Arrivals: the ones that feed the queue
Departures: the yield after service

Server

server

In a queuing system, the server represents the restriction of the system. The server is able to provide the service at a certain rate, $μ$ .

Server symbol - 02 - Fundamentals fo Queuing Theory - OMT 2024-10-26 12.17.04.excalidraw.png
%%🖋 Edit in Excalidraw%%

Server disposition

In any system, there can be more than 1 server. The $n$ servers, can be

#Servers in parallel
#Servers in series

Servers in parallel

When the servers are localized in parallel, they can work at the same time. These are differentiated based on how the queue works:

#Decentralized system
#Centralized queue

One problem that might arise with parallel service, is that the servers are not positioned in space in an efficient way. It may happen that the queue blocks some other server. This could happen, for example, at a petrol station where two pumps are one after the other and there is not enought space for cars to overtake each other.

Decentralized system

In a decentralized system, each server has its own queue.

Centralized queue

In a centralized queue, there are multiple servers but only 1 queue.

The centralized queue, if well managed, can maximize the capacity and efficiency of the system. In fact, in this case, no server will ever be idle, while there are other servers working.

It also guarantees the #First Come First Serves - FCFS functioning.

In these kind of systems, it is important to implement adequate information system that assigns customers to servers at due time. This needs to ensure that there is no idle server at any time.

This can be challenging, especially when it takes a long time for the costumer to get to the server from the end of the queue (think of container ships waiting outside a port).

Servers in series

Tandem queues

In this kind of systems costumers need to undertake several steps to receive a complete service.

For example, in an airport, a passenger has first to check-in, thank go through security, and finally queue to board the plane. Seen as a whole, this is a tandem queue.

In this scenario, the departure from the previous server, is the arrival of the subsequent one.

Storage

Arrivals

Departures

Queuing disciplines

Queuing discipline is a non-physical component of a queuing system. It refers to the rules which determine in which order the costumers are served.

The most common ones are:

#First Come First Serves - FCFS
#Last Come Last Serves - LCLS
#Service in Random Order - SIRO
#Round Robin - RR

Sometimes, there can be priorities assigned to some kind of costumers, leading to a new type of discipline:

#Early Due Date First - EDDF
#Shortest Service Time First - SSTF

First Come First Serves - FCFS

This is the most common discipline when dealing with human costumers.

first come first serves (fcfs)

In FCFS discipline, service is provided in the same order of arrivals.

This doesn't mean that the first costumer to enter will also be the first one to exit as, with #Servers in parallel, some server may be faster than another allowing for overtakes in the system.

Last Come Last Serves - LCLS

last come last serves (lcls)

In LCLS discipline, costumers are served in the reversed order of arrival.

This happens when the #Storage is in a closed space and the entrance and exit are the same "door".

For example an airport shuttle bus will unload first the passengers that boarded the bus at last and viceversa.

Service in Random Order - SIRO

service in random order (siro)

In SIRO discipline there is no preset order and the costumer is selected randomly from the queu.

This system is mostly applied to industrial processes where the costumer are different items in a production line.

Round Robin - RR

round robin - rr

In RR discipline, each costumer is assigned the same amount of service time. If the service is not completed in said time, the costumer returns back into the queue.

This discipline applies in the communication networks.

Early Due Date First - EDDF

Shortest Service Time First - SSTF

Cumulative plot

cumulative plot

A cumulative plot - $(N, t)$ diagram - plots the cumulative number of customers $N$ , to cross a specific location as a function of time $t$ .

Cumulative plot generic - 02 - Fundamentals fo Queuing Theory - OMT 2024-10-26 15.09.12.excalidraw.png
%%🖋 Edit in Excalidraw%%

Properties of the cumulative plot:

It's a discrete function
It's always increasing or, at most, constant

The flow of vehicles or passengers $q$ can be calculated starting from the cumulative plot as:

q_{(T)} = \frac{N (t_{j}) - N (t_{i})}{t_{j} - t_{i}}

where

$T = t_{j} - t_{i}$ the period of observation

The plot can be obtained in 2 ways:

Every time a customer enters the system, the time and the cumulative number of customer is recorded
Every a predefined $Δ t$ , the cumulative number of customer that entered the system in that time interval is recored

When a large number of customer is recorded, the jumps of the $N (t)$ function become meaningfulness. So, the function is usually replaced by a continuous interpolation.

In this situation, we can calculate the instantaneous flow $q_{(t)}$ as:

q_{(t)} = \frac{\partial N}{\partial t}

Input-output diagram

An input-output diagram is the overlay of 2 #Cumulative plot:

$A (t) = N (t, x_{0}) :$ cumulative plot measured at location $x_{0}$ , before the system being measured. In other words, the #Arrivals
$D (t) = N (t, x_{1}) :$ cumulative plot measured at location $x_{1}$ , after the system being measured. In other words, the #Departures
If the $A (t)$ curve is not measured exactly at the entrance of the system of interest, don't we overestimate the delay time in the system? ✅ 2024-10-29

The diagram above is an input-output diagram.

Notice that the horizontal distance between the 2 curves at a given number of cumulative costumers, $n_{1}$ , is the time spent by that costumer in the system. This time includes:

Potential delays
Free flow service time

Instead, the vertical distance between the 2 curves at a given instant $t_{1}$ , is the customer accumulation in the system. This includes:

The customer being served at the moment
The customers waiting to be served

observation

The $D (t)$ curve can never go above the $A (t)$ curve since, in order to exit, a customer has to have enter first.

It the 2 curves match, it means that the system is empty of customers.

In the diagram above, other than the input-output diagram, the amount of customers in service and in queue at any given time is also shown:

A logistic curve

We will now consider an #Input-output diagram with a large number of customers, so that the curves can be seen as continuous functions.

In the input-output diagram, the Arrival curve $A (t)$ usually takes the shape of a logistic curve.

The arrival rate is always relatively small at the two extremes while it picks in the middle (the arrival rate, $λ$ , is given by the slope of the arrival curve). This is because, as humans, we tend to want the same service at about the same time. This pick rate is theoretically unbounded.

The departure curve instead, has a fixed maximum rate, $μ$ , equal to the Capacity of the system. So, this slope is always bounded.

From a normal #Input-output diagram we can easily read the sum of the service time and delay, and the total accumulation (number of customer being served + customers queuing).

It is useful to be able to read directly the delay and the excess accumulation. This can be done through the #Virtual Arrivals Curve

3D representation of input-output diagram

If we want to visualize both vehicles trajectories and input-output diagram on the same chart, we can do so in a 3D diagram:

The projection of this diagram on the ( $x, t$ ) plane gives the trajectories, while the projection onto the $(N, t)$ plane gives the input-output diagram.

We can also look at the two projection one under the other to visualize everything on a single plane:

If at one point there is queuing (accumulation), shouldn't the $x, t$ diagram show the trajectory going horizontal for a bit? ✅ 2024-10-28
- Not necessarily: if more veh are being served and they don't need to stop, than this is correct

Virtual Arrivals Curve

virtual arrivals curve (v(t))

The Virtual Arrivals Curve is a curve obtained by moving the arrival curve ( $A (t)$ ) forward in time of an amount equal to the free flow travel time.

It can also be defined as the #Departures curve that would be measured in the absence of delay.

Virtual Arrivals curve - 02 - Fundamentals fo Queuing Theory - OMT 2024-10-26 17.14.37.excalidraw.png
%%🖋 Edit in Excalidraw%%

What we obtain:

#Excess accumulation
- #Average excess accumulation
#Delay
- #Average delay per costumer

Excess accumulation

excess accumulation ($q$)

Excess accumulation is the number of extra costumer that we have in the system due to the fact that there is a queue forming.

The Excess accumulation can be obtained as the vertical distance in the $N - t$ diagram between the #Virtual Arrivals Curve and the #Departures curve.

Average excess accumulation

We define the area

W_{1} [c u s t o m e r s \cdot t i m e]

as the total aggregated delay in the period $t_{i}, t_{j}$

average excess accumulation ($\overline{q}$)

We can calculate Average excess accumulation ( $\overset{―}{Q}$ ) in the period $t_{i}, t_{j}$ :
$\overset{―}{Q} = \frac{W_{1}}{t_{j} - t_{i}}$

Take some time to think on the meaning of the average excess accumulation:

The average excess accumulation $\overset{―}{Q}$ is always less or equal to the number of costumers that we see in the physical queue. Watch the example below to better understand this concept.

The diagram shows a stretch of road in 2 scenarios:

No queue: cars move freely at the same speed
- We count 2 veh in the area of interest (the one in the orange dashed box)
Queue: Some cars are queueing in the area of interest
- We count 5 cars

02 - Fundamentals fo Queuing Theory - OMT 2024-11-03 18.27.37.excalidraw.png
%%🖋 Edit in Excalidraw%%

Notice that, of the 5 cars in the boxed area, even without queue, there would be 2. Meaning, the excess accumulation is NOT 5, but just 3.

Delay

delay ($w$)

The Delay ( $w$ ) is the extra time a costumer has to spend in the system due to queuing.

Delay can be obtained as the horizontal distance in the $N - t$ diagram between the #Virtual Arrivals Curve and the [[#Departures]] curve.

Average delay per costumer

We define the area:$$
W_{2} \quad \rm[costumers]

as the total delay collectively incurred by customers between $n_{i}$ and $n_{j}$.  ```ad-Teo title: Average delay per costumer ($\overline{w}$)  We calculate the **Average delay per costumer** ($\overline{w}$) in the group between $n_{i}$ and $n_{j}$: $ \overline{w} = \frac{W_{2}}{n_{j}-n_{i}} $  ```  ## Little's Formula 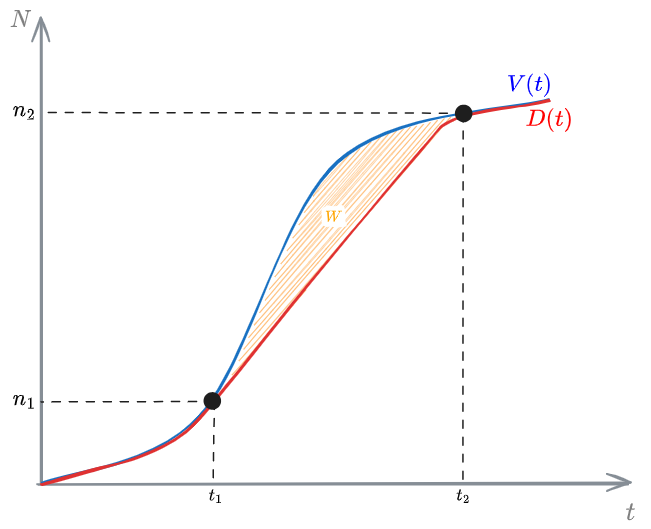 ![Little's Formula diagram - 02 - Fundamentals fo Queuing Theory - OMT 2024-11-03 18.36.38.excalidraw.png](/img/user/Excalidraw-2/Little's%20Formula%20diagram%20-%2002%20-%20Fundamentals%20fo%20Queuing%20Theory%20-%20OMT%202024-11-03%2018.36.38.excalidraw.png)   ```ad-Teo title: Little's Formula  $ \overline{\lambda} = \frac{\overline{Q}}{\overline{w}} $  **Proof:**  According to the definition, we can write for the [[#Average excess accumulation]]: $ \overline{Q} = \frac{W}{t_{2}-t_{1}} \quad \Longrightarrow \quad W =  \overline{Q}(t_{2}-t_{1}) $ and for the [[#Average delay per costumer]]: $ \overline{w} = \frac{W}{n_{2}-n_{1}} \quad \Longrightarrow \quad W =  \overline{w}(n_{2}-n_{1}) $ Meaning that: $ \overline{Q}(t_{2}-t_{1}) = \overline{w}(n_{2}-n_{1}) $ Therefore: $ \frac{\overline{Q}}{\overline{w}} = \frac{n_{2}-n_{1}}{t_{2}-t_{1}} $ where the ratio on the right-hand side is the ratio of arrival of costumer, $\lambda$. $ \frac{\overline{Q}}{\overline{w}} = \lambda  $ *q.e.d.* ```  ## Typical scenario  In a typical scenario we only have part of the data:

\begin{align}
\text{Knowns: }&
\begin{cases}
V(t): \text{Measured when there are few people} \
\mu : \text{Max service flow (it's a property of the facility)}
\end{cases} \ \

\text{Unknowns: }&
\begin{cases}
\overline{w}\
\overline{Q}
\end{cases} \quad \Longrightarrow\text{We need the }D(t)
\end

We will describe how we can construct thedeparture'scurve.  First, keep in mind these 2 properties: - $\dot{D}(t) = \mu \quad$ ff there is queue - $\dot{D}(t) = \min(\dot{V}(t), \mu)\quad$ if there is NO queue  Also, the following rules must be followed:

\begin{cases}
D(t) < V(t) \quad \forall t \
\dot{D}(t) < \mu \quad \forall t
\end

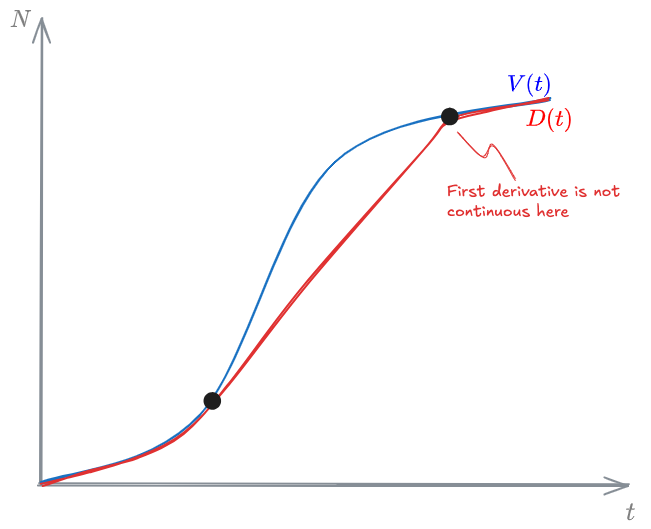![Constructing a departures curve on N-t diagram - 02 - Fundamentals fo Queuing Theory - OMT 2024-11-03 19.24.26.excalidraw.png](/img/user/Excalidraw-2/Constructing%20a%20departures%20curve%20on%20N-t%20diagram%20-%2002%20-%20Fundamentals%20fo%20Queuing%20Theory%20-%20OMT%202024-11-03%2019.24.26.excalidraw.png)   Notice how the $D(t)$ curve follows exactly the $V(t)$ curve untile the rate of arrival, $\dot{V}(t)$ is greater than the rate of service, $\mu$. From this instance, the $D(t)$ has a constant slope equal to $\mu$, until it meets back the $V(t)$, at which point it goes back to following it.    ## On-off queueing system  ### Unsaturated system  ### Exactly Saturated system  ### Overly Saturated system  ## Tandem queueing system  ### Diverging systems