01 - Introduction to trajectories Analysis - OMT
01 - Introduction to trajectories Analysis - OMT
🕒 17:30: Problem solved in class (see iPad)
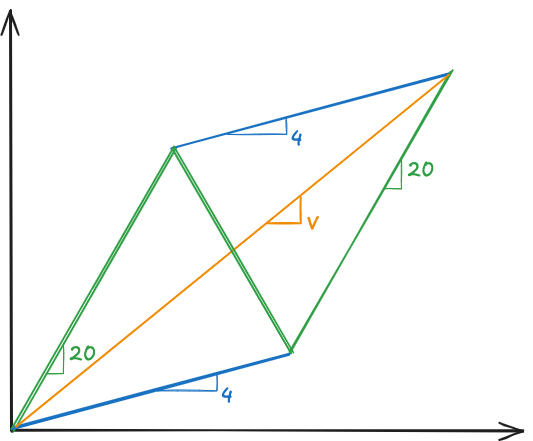
Imagine three friends who want to take a long trip using a tandem bicycle for two persons. Because the bike riders travel at 20 km/h, independent of the number of riders, and all three persons walk at 4 km/h, they proceed as follows:
- To start the journey, friends “A” and “B” ride the bicycle and friend “C” walks.
- After a while, friend “A” drops off friend “B” who starts walking and “A” rides the bicycle alone in reverse direction.
- When “A” and “C” meet, they turn the bicycle and ride forward until they catch up with “B”.
At that moment, the 3 friends have completed a basic cycle of their strategy, which they then repeat a number of times until they reach their destination. Could you determine their average travel speed?
Solution:
Trajectories of a traffic stream on a time-space diagram
When we work with time and space we use coordinated axis, with time (
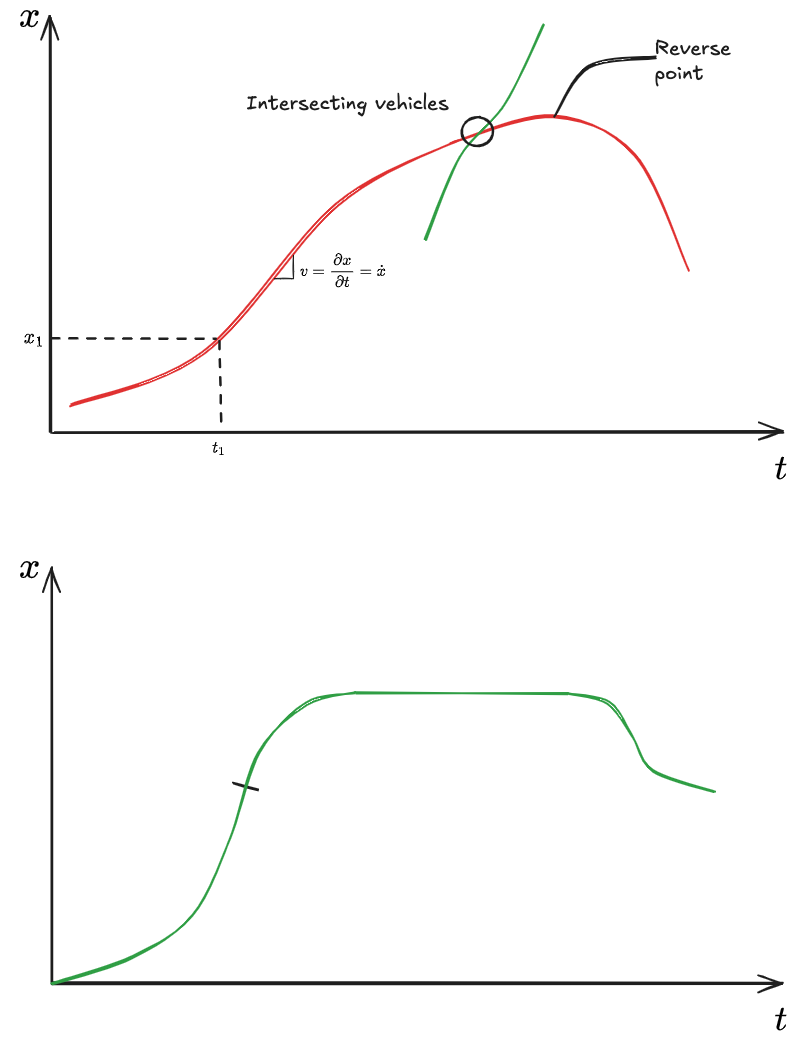
This visualisation allows to have all the main parameters readily available:
- Position
- Speed/velocity
- Acceleration
- Time
Velocity:
Acceleration:
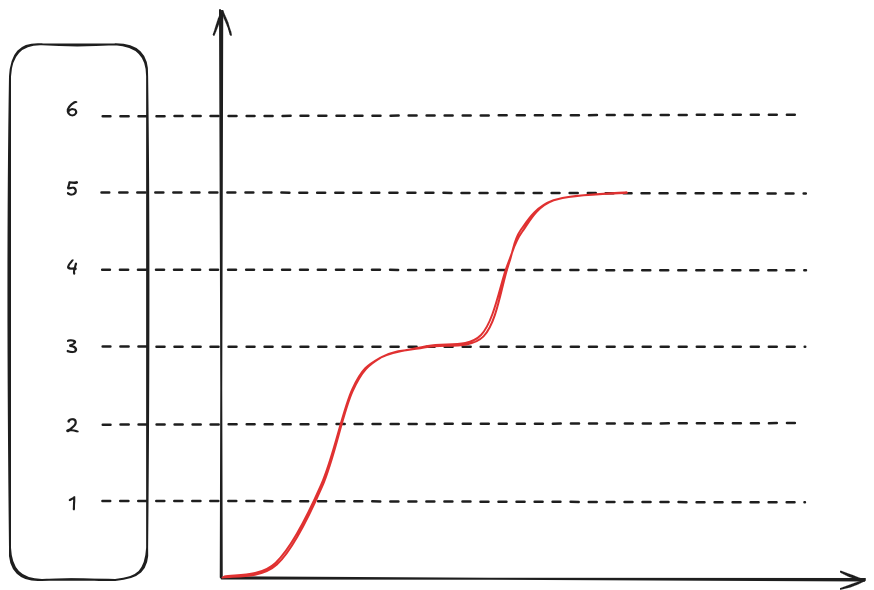
The graph shows a possible trajectory of an elevator that stops at floor 3 and 5.
Scheduling
We want to figure out the capacity of a rail line (single rail)
We have a train traveling from A to B at constant speed
Capacity is a flow:
Flow it's the number of passengers or vehicles or expeditions per hour
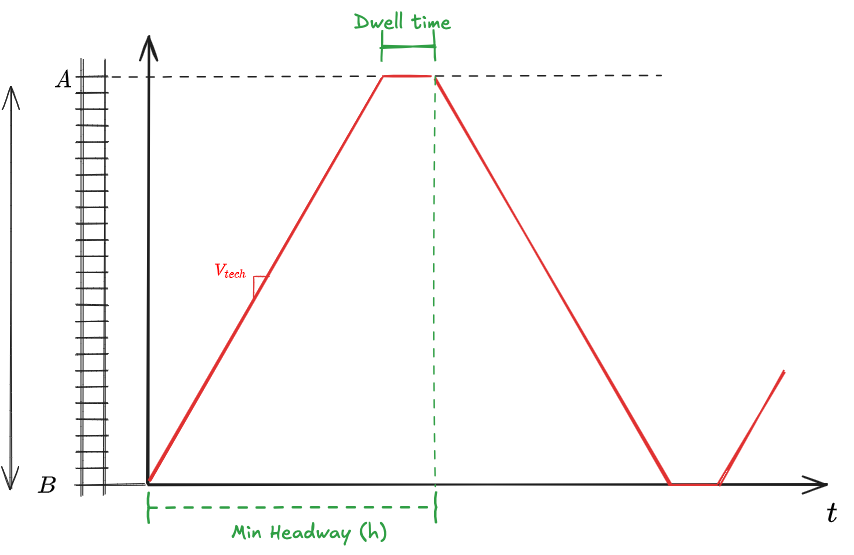
Dwell time is the time taken for passengers to board and un-board.
Headway: (
then:
We can increase capacity of the diagram above in different ways:
- Add a way for trains to pass each other in the middle: side track
- We could add more sidetracks but it becomes a problem of controlling the switches. If any train is delayed, then every train gets delayed
- Faster trains would allow for shorter headways
- Have more tracks at the ends so we can have train ready to leave as soon as one arrives

Constructing trajectories
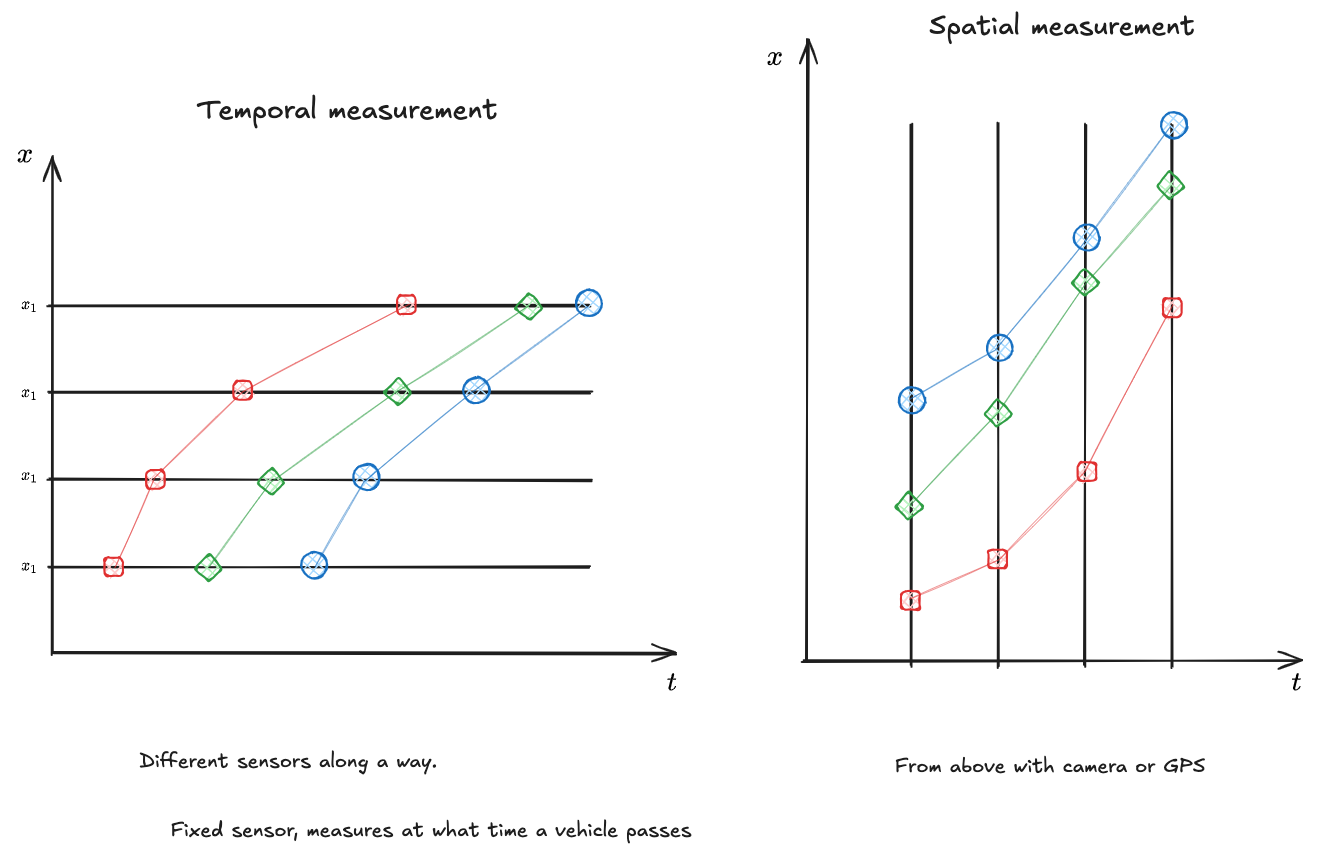
Traffic stream properties
- macro - micro - time vs space average
Flow
We can define the flow - MACROscopic variable:
where:
: # of vehicles : time
Can be written as:
also
Flow is equal to the inverse of the average headway:
The headway is considered a microscopic variable.
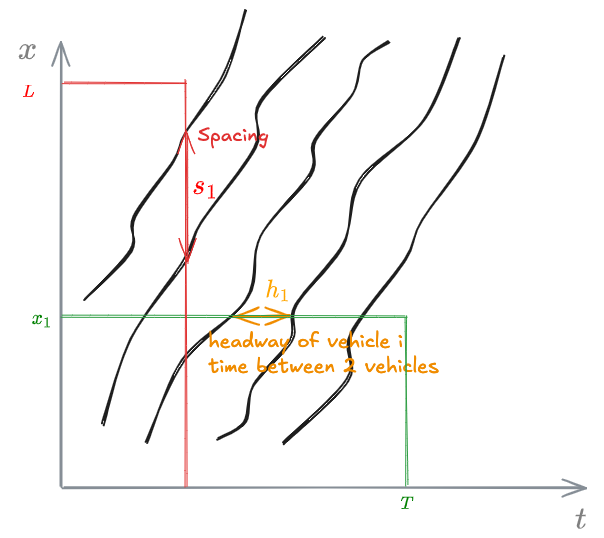
Spacing
If we count the number (
And can also write:
Speed
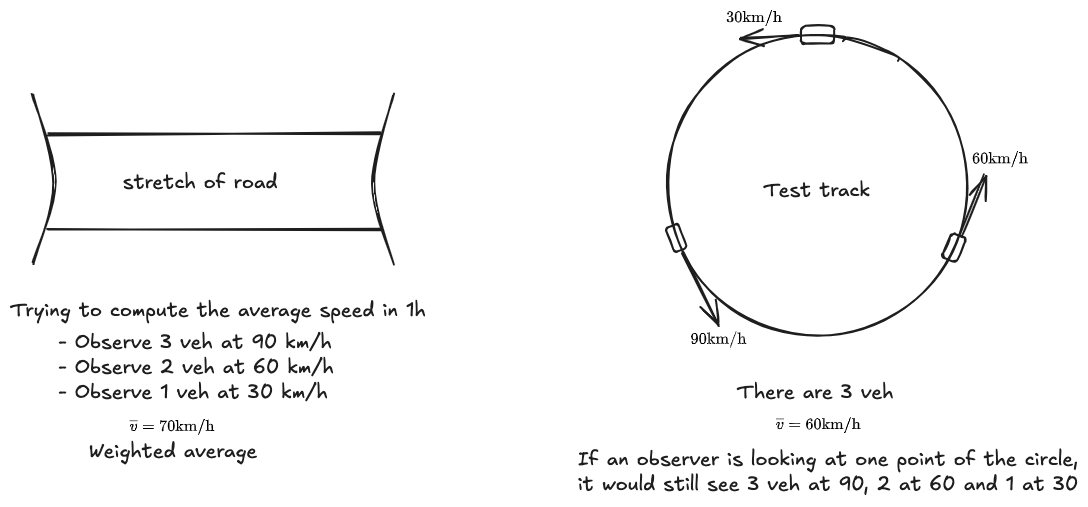
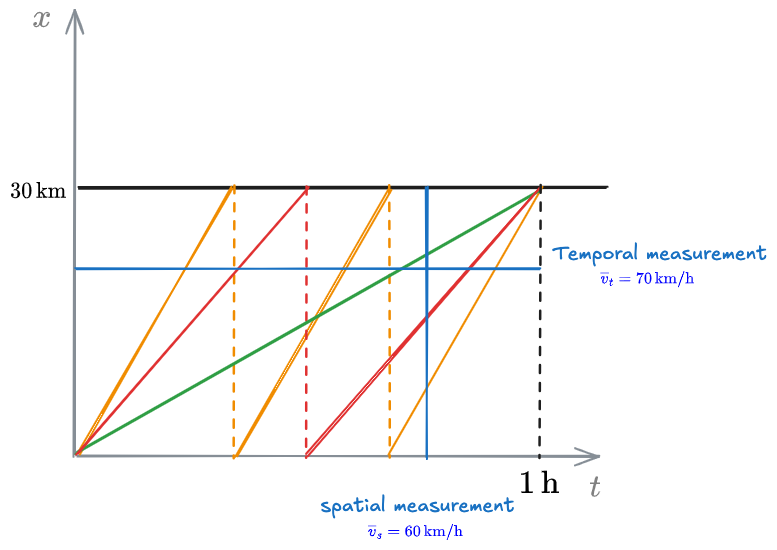
The difference is that in one case we're measuring
Let
If I multiply everything by
For spatial:
Fundamental equation of traffic
Stationary traffic
You can measure any value anywhere and it's always the same.
The only way is to have parallel trajectories that are equidistant.
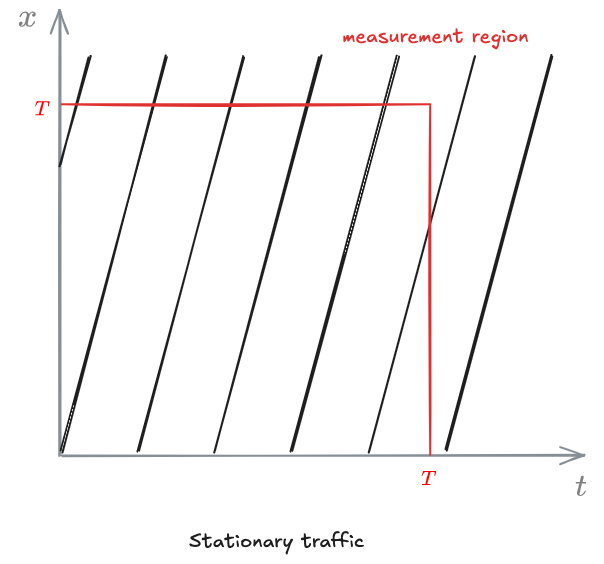
then
This is true for stationary traffic.
Also:
It's also true for any kind of traffic:
❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗