Traveling Salesman Problem

traveling salesman problem

The Traveling Salesman Problem consists in solving the following:

Given a complete graph, with $n$ nodes, and the cost of traveling between each and every pair of nodes, what is the shortest possible route that visit each node only once and returns to the initial node?

The following elements come into play:

$K_{n} :$ the complete graph with $n$ nodes, where $V$ is the set of nodes and $| V | = n$
$c_{i j} :$ cost associated with link $(i, j)$
$x_{i j} :$ decision variable - equals 1 if link $(i, j)$ is used in the solution, 0 otherwise
Objective: find an Hamiltonian circuit of minimum cost when the cost of a circuit is the sum of the costs of the links defining the circuit

Formulation of the TSP

There exist several formulations for the TSP.

Basic TSP formulation

A basic formulation of the [[#Traveling Salesman Problem]] is the following:

basic traveling salesman problem formulation

$min_{x_{i j}} \sum_{(i, j) \in A} c_{i j} x_{i j}$
subject to:
$Degree constraints: {\begin{cases} \sum_{j \in A^{+} (i)} x_{i j} = 1, \forall i \in V \\ \sum_{j \in A^{-} (i)} x_{i j} = 1, \forall i \in V \end{cases}$
where:

$x_{i j} \in {0, 1}, \forall (i, j) \in A$
- $x_{i j} = 1$ if link $(i, j)$ is used in the solution, 0 otherwise

DEGREE CONSTRAINTS:
The degree constraints are needed to ensure that every node has only one link entering it and one exiting it.

More specifically:

$A^{+} (i) = {j | (i, j) \in A} :$ set of all links entering node $i$
$A^{-} (i) = {j | (j, i) \in A} :$ set of all links exiting node $i$

This formulation is not sufficient to define the problem. In fact, a possible solution with this formulation could give something like this:

Schermata 2024-12-27 alle 17.25.03.png

In the solution shown above, we can see that every link is only visited once, and the cost was minimized. We can easily see thoug that many subtours were made in place of a single tour.

TSP formulation with subtours breaking constraints

In order to avoid subtours like the one originating from the [[#Basic TSP formulation]], a new constraint is added to the formulation:

traveling salesman problem formulation with subtours breaking constraints

$min_{x_{i j}} \sum_{(i, j) \in A} c_{i j} x_{i j}$
subject to:
$
\begin{align}
\text{Degree constraints:} &\begin{cases}
\sum\limits_{j \in A^{+}(i)} x_{ij} = 1, \qquad \forall i \in V \
\sum\limits_{j \in A^{-}(i)} x_{ij} = 1, \qquad \forall i \in V \
x_{ij} \in {0,1}, \qquad \forall (i,j) \in V
\end{cases} \ \

\text{Subtour breaking constraint:} &\sum\limits_{i\in S, j \in S} x_{ij} \le |S| - 1, \qquad \forall S \ne 0, \quad S\subset V
\end{align}
$
where:

$x_{i j} \in {0, 1}, \forall (i, j) \in A$
- $x_{i j} = 1$ if link $(i, j)$ is used in the solution, 0 otherwise
$S :$ is a subset of all the nodes ( $V$ )

Remember:

$A^{+} (i) = {j | (i, j) \in A} :$ set of all links entering node $i$
$A^{-} (i) = {j | (j, i) \in A} :$ set of all links exiting node $i$

SUBTOUR BREAKING COSTRAINT:
The subset breaking constraint does the following: for any subset of nodes, the number of links connecting these nodes has to be lower or equal the number of nodes in the subset minus 1. With this constraint, if $S \equiv V$ , than a tour connecting all nodes will necessarily have $| V | - 1$ links. If, for example, I was to take a subset, $S$ , with only 3 nodes, and these 3 nodes where connected to each other in a cycle, the cycle would contain 3 links, but this would break the constraint. So, if we check this condition for every possible subset of $V$ , we will be sure that no subtour is created.

Despite this constraint being theoretically acturate, and it would allow to come to the right solution to the problem, given a network with $n$ nodes, the constraints needed would amount to
$2^{n - 1}$
conditions. These, is way too many for any computer when $n$ approaches values of any significance.

TSP formulation with weak subtour breaking constraints

Since, as we've seen in [[#TSP formulation with subtours breaking constraints]], the formulation of the breaking constrains is highly impractical when it comes to solving the problem with a computer, we hereby propose an alternative formulation.

traveling salesman problem formulation with weak subtours breaking constraints

$min_{x_{i j}} \sum_{(i, j) \in A} c_{i j} x_{i j}$
subject to:
$\begin{aligned} Degree constraints: & {\begin{cases} \sum_{j \in A^{+} (i)} x_{i j} = 1, \forall i \in V \\ \sum_{j \in A^{-} (i)} x_{i j} = 1, \forall i \in V \\ x_{i j} \in {0, 1}, \forall (i, j) \in V \end{cases} \\ Weak Subtour breaking constraint: & {\begin{cases} u_{j} \geq u_{i} - n (1 - x_{i j}) + 1, i \neq j, i \neq 1 \\ u_{1} = 1 \\ 1 \leq u_{i} \leq n, \forall i \in V \end{cases} \end{aligned}$
where:

$x_{i j} = 1$ if link $(i, j)$ is used in the solution, 0 otherwise

Remember:

$A^{+} (i) = {j | (i, j) \in A} :$ set of all links entering node $i$
$A^{-} (i) = {j | (j, i) \in A} :$ set of all links exiting node $i$

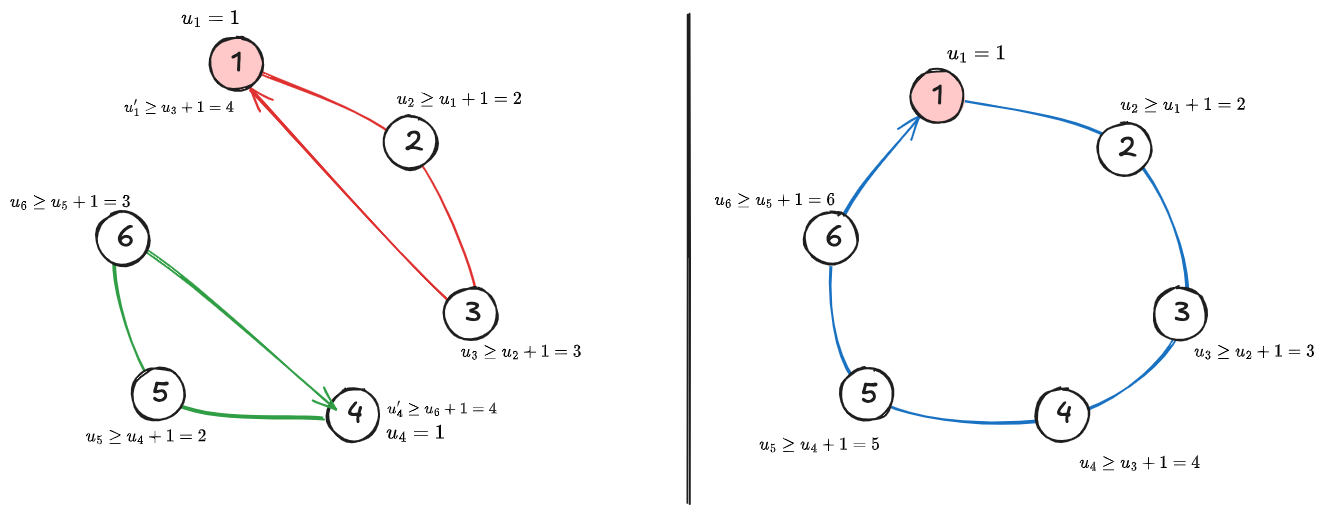
Explanation of the WEAK SUBTOUR BREAKING CONSTRAINT
$u_{i}$ is a variable that allows to avoid subtours in the solution. Notice how $u_{j}$ must be greater than a certain quantity, specifically $u_{j} \geq u_{i} + 1$ for links in the solution, except for when $i = 1$ . $i = 1$ is the depot. This means that, the only occasion where $u_{j}$ can be lower than $u_{i} + 1$ is when we go back to the depot. It is therefore impossible for the problem to generate subtours. In fact, that would mean that a cycle is created but in order for that to happen, $u_{j}$ would be greater than $u_{i} + 1$ when $i$ is not 1. Here is an attempt of a visual representation of how this constraint works:

%%Edit in excalidraw%%

The figure above shoes the same network with 2 different solutions to the TSP. Keep in mind only the links in the solution are shown, the network is supposed to be complete.

On the left, the solution breaks the the weak subtour breaking constraints. In fact, $u_{1}^{'} \geq 4$ and $u_{1} = 1$ is suppsed to be a contraddiction: in fact a number cannot be greater than 4 and equal to 1 at the same time (the prime notation is just to show that it is obtained following the cycle). This is allowed since for $i = 1$ the constraint is not valid. Notice though how the same happens in the green cycle at node 4. This time though this disrepancy is not allowed, therefore, this solution is not permitted.

On the write, a unique cycle where the only occasion where the constraint is broken is when it is actually allowed, at $i = 1$ .

Solving the TSP

Solving the [[Traveling Salesman Problem]] is no easy task. That is why the problem is most often approached through [[Heuristic]] methods.

These are methods that are not proven to be mathematically optimised (as a matter of fact, they are not), but rather use an intuitive approach to reach a solution that is, at the very least, good enough. They won't guarantee to approach the exact solution, but should be able to provide a solution that is not far from it.

We will see the following:

[[#Nearest neighbour heuristic]]
[[#Nearest neighbour insertion heuristic]]
[[#Spanning tree heuristic]]
[[#Christofides heuristic]]
[[#Improvement heuristics]]

For any of the following method, a cost matrix is going to be needed. This is a matrix that, for each link, gives the cost of traveling on that link.

Nearest neighbour heuristic

The nearest neighbour heuristic is considered a [[greedy heuristic]].

nearest neighbour heuristic

To approach a solution this is how we proceed:

Select a node $i \in N$ in the network. Label this node as to remember that has already been visited;
Look at all the links leaving node $i$ and select the one with the lowest cost;
Follow the selected link to $j$ and label it too;
Keep going like this until all nodes have been labeled.

We can think of labelling a node as to add it to a set $T$ . Whenever we look for a new link, we will only check links the go to a node that is not yet in $T$ .

When all nodes are in $T$ , we stop as we will have obtained a [[Hamiltonian circuit]].

Nearest neighbour insertion heuristic

The nearest neighbour insertion heuristic is considered a [[greedy heuristic]].

nearest neighbour insertion heuristic

Select any initial subtour. The nodes in the subtour will go into a set $C$
For every $i^{t h}$ node not in the subtour, create a set, $d (i, C)$ containing all costs from and to that node $i$ to every node in the subtour ( $C$ )
- we will have something like: $d (i, C) = {c_{i 1}, c_{i 2}, . . ., c_{i n}}$ for each node $i \notin C$
Select the minimum cost of each set $d (i, C)$ : $min_{j \in C} (d (i, C))$
Select the minimum of all the costs found in step 3
Add the selected link to the subtour and repeat the steps

Spanning tree heuristic

To apply the spanning tree heuristic, a complete graph is needed: $K_{n} = (V, A)$ (where: $V$ -set of links and $A$ -set of nodes).

spanning tree heuristic

Find a minimum spanning tree of $K$ --> $S T$
Double all arcs in $S T$ , generating an auxiliary graph: $(V, S T)$
Since each node has even degree, an Eulerian cycle exists
1. Determine an Eulerian cycle: $C$
2. Assign an orientation to $C$
3. Select a starting node $i$
Make a Hamiltonian cycle following the nodes in the order of the Eulerian cycle. whenever a node already visited should be selected, jump to the first available node in the Eulerian cycle
Stop when the Hamiltonian cycle is complete

Finding a Minimum Spanning Tree - Prim's Algorithm

prim's algorithm

Select an arbitrary node in the network
Select the arc with the minimum cost among those that connect any node already in the ST to any node not yet in the spanning tree
Repeat until the Spanning Tree contains all nodes in the network

Christofides heuristic

christofides heuristic

Determine a Minimum Spanning Tree $S T$ of $K_{n}$
Find all nodes with odd degree and find a Minimum Perfect Matching, $M$
Make a new graph, $H$ , out of all the edges in $S T$ and $M$
Form an Eulerian cycle in $H$ and orient it arbitrarily
Make a Hamiltonian cycle following the nodes in the order of the Eulerian cycle. whenever a node already visited should be selected, jump to the first available node in the Eulerian cycle
Stop when all nodes are part of the Hamiltonian cycle.

Improvement heuristics

In the heuristics described above, it is rare to find an optimal solution. They are, in general, of moderate quality. Therefore, we pose the question of how we can improve a Hamiltonian cycle found in one of the previous heuristic.

We will see the [[#Exchange Heuristic]]. This is quite intuitive to understand if we're looking at an Euclidean problems. In a Euclidean problem, the distance between 2 nodes is given simply by the Euclidean distance between the nodes (basically, the real distance in any geometric space).

In this case, whenever a Hamiltonian cycle crosses itself, there must exist a better path, without crossings. What we will do is to unfold the path where it crosses itself in order to have a lower cost.

In a general problem (not euclidean), we can't really think in terms of unfolding a crossing, but the concept stays the same. We'll try to exchange some links in order to bring the cost between 2 nodes down. This is what we do in the [[#Exchange Heuristic]]

Exchange Heuristic

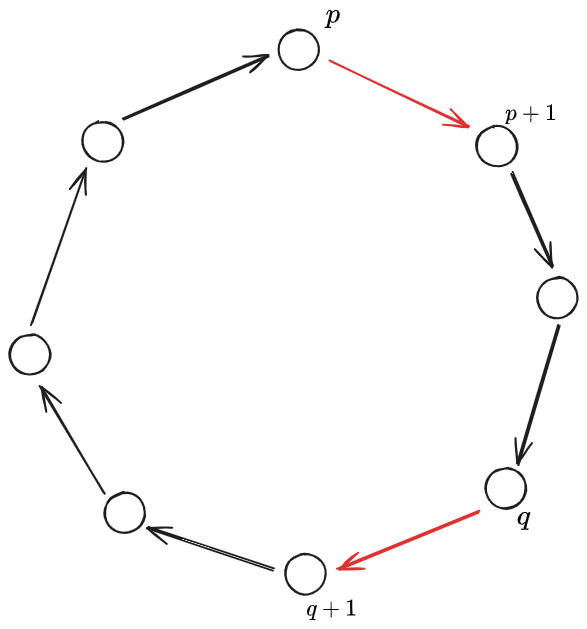
Suppose we have a Hamiltonian cycle like the following:

%%🖋 Edit in Excalidraw%%

We are interested in links: $(i_{p}, i_{p + 1})$ and $(i_{1}, i_{q + 1})$ .

The heuristic goes as follow:

Choose any vertex $i$
Pick a pair of links such that they fall into the set $Z$ :

Z := {(i_{p}, i_{p + 1}), (i_{q}, i_{q + 1}) | p + 1 \neq q, p \neq q, q + 1 \neq p, 1 \leq p, q \leq n}

which means any pair of links such that they have at least one other link in between them.
3. For each pair in $Z$ check if

c_{p, p + 1} + c_{q, q + 1} > c_{p, q} + c_{p + 1, q + 1}

then remove links $(i_{p}, i_{p + 1})$ and $(i_{1}, i_{q + 1})$ from the solution and add $(i_{p}, i_{q})$ and $(i_{p + 1}, i_{q + 1})$ .
Repeat for every node in the network.

%%🖋 Edit in Excalidraw%%

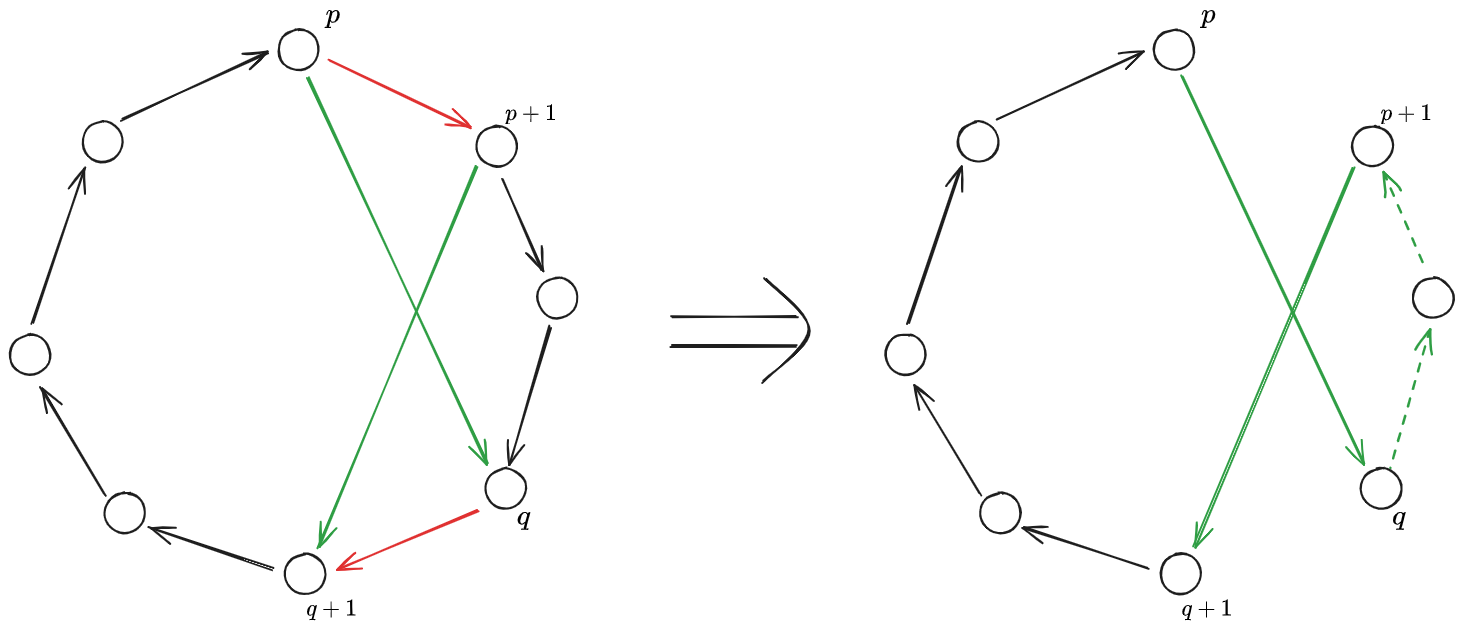
In the example we compare the cost of having the green links in place of the red ones. Since the cost is lower for the green pair, then we exchange them. Notice how we also need to switch the direction of the dashed links in order to keep the directed hamiltonian cycle.

asymmetric graphs

In case of asymmetric graphs, we also need to check and compare the costs of the links we do not intend to exchange but that we need to reverse. It would become:
$c_{p, p + 1} + c_{q, q + 1} + c_{p + 1, q} > c_{p, q} + c_{p + 1, q + 1} + c_{q, p + 1}$
where the orange costs are the total costs to go from node $p + 1$ to node $q$ (with all the intermediate links taken into account) and viceversa.