04 - Vehicle Routing problem - MM

The Capacitated Vehicle Routing Problem - CVRP

In a system, we identify 1 depot and many clients. Given $k$ trucks (or delivery vehicle in general), we want to assign every client to a track and then define a cycle route from and to the depot, that the truck has to follow in order to deliver to every client, minimizing the total cost.

%%🖋 Edit in Excalidraw%%

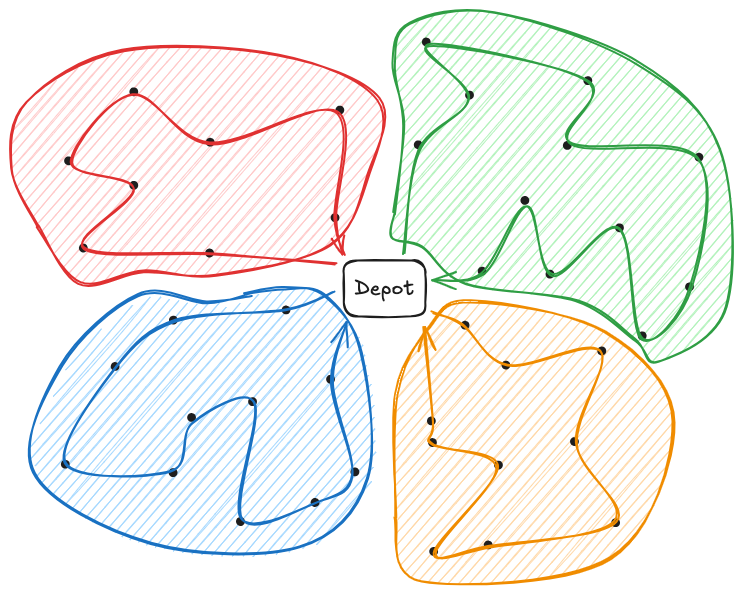
for example, given the situation above (imaiginig that all points are nods of a complete graph), we wnat to get a solution like:

%%🖋 Edit in Excalidraw%%

In the graph above, each color represent a transportation unit.

What we want to achieve in the Capacitated Vehicle Routing Problem, is to:

Assign each client to one transportation unit
Create the best route for each transportation unit

Overview of CVRP

As we will see, the problem is formulated as a binary linear programming problem.

Since the CVRP is a quite difficult problem to both formulate and solve, the common approach is to first work on an simpler problem, known as the Traveling Salesman Problem

Before continuining reading this note, it is higly suggested to read the Traveling Salesman Problem, if you're not yet familiar with it and with the methods to solve it.

Characteristics of CVRP

Each costumer is visited exactly once by one vehicle
The route of each vehicle starts and ends at the depot
The sum of demands of costumers on a route must not exceed vehicle's capacity

CVRP formulations

We will give several formulations of the Capacitated Vehicle Routing Problem.

Conceptually we could define the problem in 2 parts:

Assigning clients to trucks - #CVRP formulation in terms of linear generalised assignment problem
Optimizing routes

CVRP formulation in terms of linear generalised assignment problem

We first give a formulation of a problem that would allow to assign clients to a route efficiently.

Let's first define the variables and parameters needed in this formulation.

Paramters:

Suppose we have $n$ clients. Each client will be named $i = 1, . . ., n$ .
There is one depot, at $i = 0$
There are $K$ delivery vehicles (trucks) available. Each one is called $k = 1, . . ., K$
$C_{k}$ is the capacity of vehicle $k$
$a_{i}$ is the amount of goods that client $i$ requires

Decision Variable:
$y_{i k}$ is the decision variable. It's a binary variable:

y_{i k} = {\begin{cases} 1, if client i is visited by truck k \\ 0, otherwise \end{cases}

Objective function:

\sum_{k} f (y_{k})

where $f (y_{k})$ is the cost of an optimal [[Traveling Salesman Problem]] tour for all clients served by truck $k$ . We are not able to provide an explicit formulation of the objective function without solving the problem first, since it requires the clients to be assigned already and tours to have been made.

The formulation of the problem would therefore become:

min_{y_{k}} \sum_{k} f (y_{k})

subject to:

\begin{aligned} Capacity constraint: & \sum_{i} a_{i} y_{i k} \leq C_{k}, \forall k = 1, . . ., n \\ Degree constraint: & \sum_{k} y_{i k} {\begin{cases} K, i = 0 & Depot \\ 1, \forall i = 1, . . ., n & Clients \end{cases} \\ y_{i k} = {0, 1}, i = 0, . . . n, k = 1, . . ., K \end{aligned}

Fisher & Jaikumar's Heuristic

To solve the problem in #CVRP formulation in terms of linear generalised assignment problem that we don't know how to write the objective function explicitly, we can try to brute force it to be a linear function, making the problem the following:

min_{y_{k}} \sum_{k} d_{i k} y_{i k}

subject to:

\begin{aligned} Capacity constraint: & \sum_{i} a_{i} y_{i k} \leq C_{k}, \forall k = 1, . . ., n \\ Degree constraint: & \sum_{k} y_{i k} {\begin{cases} K, i = 0 & Depot \\ 1, \forall i = 1, . . ., n & Clients \end{cases} \\ y_{i k} = {0, 1}, i = 0, . . . n, k = 1, . . ., K \end{aligned}

where the $d_{i k}$ coefficient are estimated as
❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗ I don't get how they are estimated
❗❗❗❗❗❗❗❗❗❗❗❗

CVRP Basic formulation

A basic formulation of the CVRP is the following:

min \sum_{i \in V} \sum_{j \in V} c_{i j} x_{i j}

Subject to:

\begin{aligned} Clients degree constraints: & {\begin{cases} \sum_{i \in V} x_{i j} = 1 \forall j \in V ∖ {0} entering node i \\ \sum_{j \in V} x_{i j} = 1 \forall i \in V ∖ {0} exiting node i \end{cases} \\ Depot degree constraints: & {\begin{cases} \sum_{i \in V} x_{i 0} = K & enterint depot \\ \sum_{j \in V} x_{0 j} = 0 & exiting depot \end{cases} \end{aligned}

❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗ The problem formulation is missing some conditions

CVRP Motzin Tucker Ziplin (MTZ) formulation

An other useful formulation of the Vehicle Routing Problem is the Motzin Tucker Ziplin formulation, also known as the MTZ formulation.

min_{x, u} \sum_{i \in V} \sum_{j \in V} c_{i j} x_{i j}

Subject to:

\begin{aligned} Clients degree constraints: & {\begin{cases} \sum_{i \in V} x_{i j} = 1 \forall j \in V ∖ {0} entering node i \\ \sum_{j \in V} x_{i j} = 1 \forall i \in V ∖ {0} exiting node i \end{cases} \\ Depot degree constraints: & {\begin{cases} \sum_{i \in V} x_{i 0} = K & enterint depot \\ \sum_{j \in V} x_{0 j} = K & exiting depot \end{cases} \\ Subtour breaking constraint: & u_{j} \geq u_{i} + a_{j} - C (1 - x_{i j}) i \neq 0, j \neq 0 \\ a_{i} \leq u_{i} \leq C i \in V \\ x_{i j} \in {0, 1} \end{aligned}

where:

$a_{i} :$ demand of client $i$
$C :$ vehicle capacity

Clarke & Wright savings heuristic

Formula for savings:

s_{i j} = c_{i 0} + c_{0 j} - c_{i j} \forall i, j = 1, . . ., n i \neq j

❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗