01.2 - The minimum cost flow problem - From book - MM

Link to chapter: Intrudoction to Operations Research - Network Optimization Models, pag 358

Introduction

The minimum cost flow problem is described as:

The network is a directed and connected network
At least one is a supply node
At least one node is a demand node
All the remaining nodes are transshipment nodes
Flow through an arc is allowed only in the direction indicated by the arrowhead. The maximum amount of flow is given by the capacity of that arc
The network has enough arcs with sufficient capacity to enable all the flow generated at the supply nodes to reach all the demand nodes
The cost of the flow through each arc is proportional to the amount of that flow, where the cost per unit flow is known
The objective is to minimize the total cost of sending the available supply through the network to satisfy the given demand. (An alternative objective is to maximize the to- tal profit from doing this)

[?] Are we not using the point number 7 in our definition of the problem?

Problem Definition

We consider a directed and connected network where the $n$ nodes include at least one supply node and at least one demand node. The decision variables are:

x_{i j} = Flow through arc i \to j

Known information:

$c_{i j} :$ cost per unit flow through the arc $i \to j$
$u_{i j} :$ arc capacity for arc $i \to j$
$b_{i} :$ net flow generated at node $i$

The value of $b_{i}$ depends on the nature of node $i$ :

$b_{i} > 0$ if node $i$ is a supply node
$b_{i} < 0$ if node $i$ is a demand node
$b_{i} = 0$ if node $i$ is a transshipment nodes

Objective: Minimize the total cost os sending the available supply through the network to satisfy the given demand.

The linear programming formulation of this problem is given as:

minimum cost flow problem

$Minimize Z = \sum_{i = 1}^{n} \sum_{j = 1}^{n} c_{i j} x_{i j}$

subject to

\sum_{j = 1}^{n} x_{i j} - \sum_{j = 1}^{n} x_{j i} = b_{i}, \forall nodes i

where:

$\sum_{j = 1}^{n} x_{i j} :$ total flow out of node $i$
$\sum_{j = 1}^{n} x_{j i} :$ total flow into node $i$
and subjet to

0 \leq x_{i j} \leq u_{i j} \forall arcs i \to j

Sometimes, it is necessary to have a lower bound constrain in the flow:
$L_{i j} > 0$
If this is the case, the problem can be easily reformulated translating the variables of the quantity $L_{i j}$ :
$x_{i j}^{'} = x_{i j} - L_{i j}$
in order to convert the problem back to the form where there is a non negativity constrain

Feasibility necessary condition

feasibility necessary condition

A necessary (but not sufficient) condition for a minimum cost flow problem to have any feasible solutions is that:
$\sum_{i = 1}^{n} b_{i} = 0$

This means that the total flow generated at the supply nodes equal the total flow being absorbed at the demand nodes.

If the condition is not met, a possible solution is to add a dummy demand node to absorb the excess supply. This node should be connected to the supply nodes with arcs of cost $c_{i j} = 0$ .

Integer solution property

integer solution property

For minimum cost flow problems where every $b_{i}$ and $u_{i j}$ have integer values, all the basic variables in every basic feasible (BF) solution (including an optimal one) also have integer values.

Example

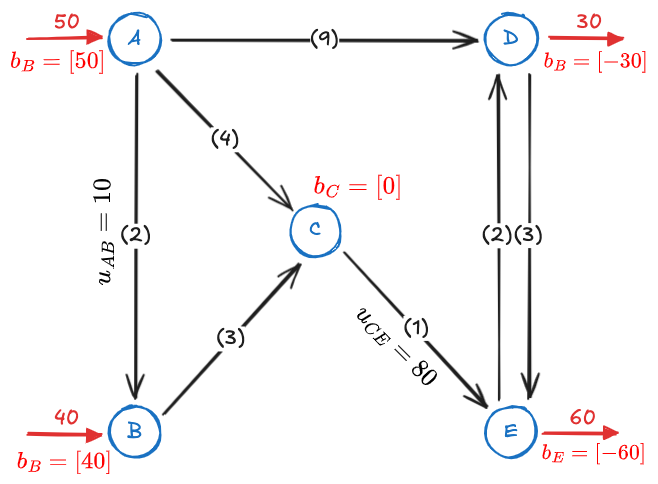
The network below is given as an example

01.2 - The minimum cost flow problem - From book - MM 2024-10-30 19.01.00.excalidraw.png
%%🖋 Edit in Excalidraw%%

The number in parenthesis on the arrows are the cost in 100€/unit.

A and B are the supply nodes, while D and E are the demand nodes.

For practical purposes, all $u_{i j} = \infty$ except for arcs:

$A \to B$ where $u_{A B} = 10$
$C \to E$ where $u_{C E} = 80$
these values are lower than the total units produced (90).

If we calculate the total cost we would obtain:
$Z = 2 x_{A B} + 4 X_{A C} + 9 x_{A D} + 3 x_{B C} + x_{C E} + 3 x_{D E} + 2 x_{E D}$
subject to the following constraints:
${\begin{cases} x_{A B} & + & x_{A C} & + & x_{A D} & + & 0 & + & 0 & + & 0 & + & 0 & = & 50 \\ - & x_{A B} & + & 0 & + & 0 & + & x_{B C} & + & 0 & + & 0 & + & 0 & = & 40 \\ 0 & - & x_{A C} & + & 0 & - & x_{B C} & + & x_{C E} & + & 0 & + & 0 & = & 0 \\ 0 & + & 0 & - & x_{A D} & + & 0 & + & 0 & + & x_{D E} & - & x_{E D} & = & - 30 \\ 0 & + & 0 & + & 0 & + & 0 & - & x_{C E} & - & x_{D E} & + & x_{E D} & = & - 60 \end{cases}$
and subject to:
$x_{A B} \leq 10 x_{C E} \leq 80 x_{i j} \geq 0 \forall i, j$

Any of the node constraints is redundant, assuming a feasible solution exists.

The Network SIMPLEX method

Pag. 389

The Network SIMPLEX method is a streamlined version of The SIMPLEX Method for solving minimum cost flow problmes. It goes through the same steps:

Finding the entering basic variable
Determining the leaving basic variable
Solving for the new BF solution
in order to move from the current BFS to a better adjacent one.

Correspondence between BFS and Feasible Spanning Trees

Given a tree with $n$ nodes, there exists a set of $n - 1$ basic variables that make up the basic feasible solution.

| I_{B} | = n - 1

The $n - 1$ arcs are referred to as basic arcs.

The rest of the arcs, with flow $x_{i j} = 0$ , are referred to as non-basic arcs.

It can be shown that a set of basic arcs always form a spanning tree. Therefore, a spanning tree can be obtained as follows:

For the arcs NOT in the spanning tree (non-basic arcs), set the corresponding variables $x_{i j} = 0$
For the arcs in the spanning tree (basic arcs), solve for the corresponding variables $x_{i j}$ in the system of linear equations provided by the node constraints

It needs to be mentioned that the solution obtained as such may not be feasible. Therefore, it is necessary to define a feasible spanning tree as one whose solution from the node constraints also satisfies all the other constraints.

fundamental theorem for the network simplex method

The basic solutions are spanning tree solutions (and conversely), and the BFS are solutions for feasible spanning trees (and conversely).