01.2 - The min-cost flow problem - from slides - MM

A network like the one below is given:

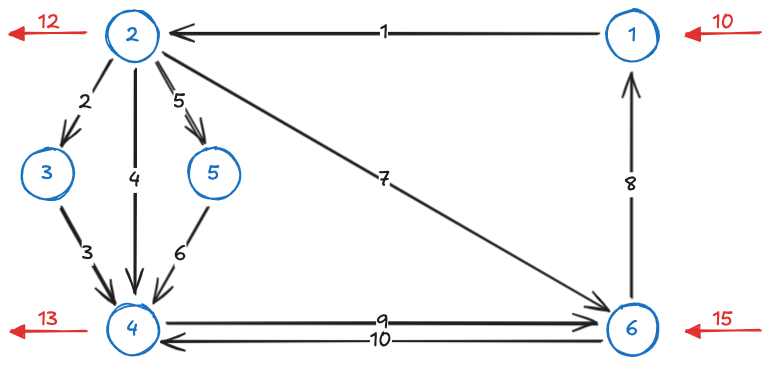
The same network, can also be described through 6 linear equations:

or in matrix form:

The flow vector, $x$, is unknown.

Given we have more unknown variables than equations, the solution won't be unique.

Problem definition

Usually, $l_{ij}=0\mathrm{\forall }(i,j)$. If this is not the case, it is easy to reformulate the problem defining a new flow vector $y$

Typically, $c_{ij}\ge 0$.

Problem solution

Basic Feasible Solution

In a min-cost flow problem, a Basic Feasible Solution is a solution to the problem that follows the following conditions.

• It's a solution
• It's feasible
• Can be split into the following sets...

Set $I_B$

Let $N$ be the number of nodes, the set $I_B$ must have cardinality:

Moreover, links in $I_B$ must make up a spanning tree.

All other links need to go in one of the following sets: $I_N$ or $I_{N^{-}}/I_{N^{+}}$.

If the problem is unbounded ($u_{ij}>\mathrm{\infty }$), all remaining links $(i,j)$, with flow $x_{ij}=0$ go into $I_N$:

If the problem is bounded, we need to split all remaining links in one fo the two sets:

Optimal solution

In order to define a #Condition of optimality we first need to introduce two concepts:

• #Dual variable
• #Reduced cost

The optimal solution to the The min-cost flow problem can be found through the The SIMPLEX Method

Dual variable

A dual variable is a value ${\lambda }_r$ that tells what is the unit cost of moving from a predefined root node to any node $r$ in the network.

1. Choose one node as the root node, $i=O$
2. ${\lambda }_r=0-c_{O,r}$
3. The value of the dual variable at node $r$ is the difference between the value of the dual variable of the previous node of the spanning tree and the cost of the link from the previous node to $r$

Reduced cost

The reduced cost ($r_{ij}$) of link $(i,j)$ is an index that tells of how much the unit cost of the network would go down or up if link $(i,j)$ was added to the solution.

• $r_{ij}=0$: Adding flow on link $(i,j)$ won't change the cost in the network
• $r_{ij}>0$: Adding flow on link $(i,j)$ will increase the cost in the network
• $r_{ij}<0$: Adding flow on link $(i,j)$ will decrease the cost in the network

The reduced cost can be calculated as:

Condition of optimality

This means that, if one of the conditions above is not met by our solution, we can say that the solution is not optimal.

Finding the optimal solution

Basic feasible solution

Each problem defined as in #Problem definition, has many possible solutions. We are interested in some specific ones, called basic feasible solutions.

Let there be a graphgraph $G=(N,A)$. Let $x_{ij}$ with $(i,j)\in A$ be a feasible flow of given graph.

The solution, $x_{ij}$ is a basic feasible solution if it falls under the following conditions:
0. It's feasible

1. We can build a set, $I_B$, so that $|I_B|=|N|-1$ containing links where the flows in the graph are equal to:
   • $x_{i,j}=0\vee x_{i,j}=u_{i,j}\vee 0<x_{i,j}<u_{i,j}$
2. $I_B$ constitutes a spanning tree
3. We put every other null or upper bound flow in other sets, $I_N$ or $I_{N+}\vee I_{N-}$

where:

• $I_{N-}=$ Set of links with null flows: $(i,j)\in I_{N-}$, then $x_{i,j}=0$
• $I_{N+}=$ Set of links with upper bound flows: $(i,j)\in I_{N+}$, then $x_{i,j}=u_{i,j}$
  or, alternativly, if there is NOT an upper bound, we only have $I_N$:
• $I_N=$ Set of links with null flows: $(i,j)\in I_N$, then $x_{i,j}=0$

$I_N$, $I_{N+}$ and $I_{N-}$ don't have to contain all the links.

Given this graph:

We can define $I_B$ as

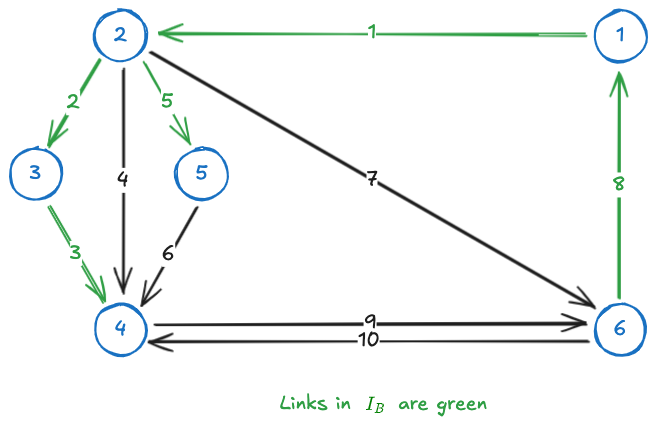
Notice that:

and that the links in $I_B$ form a spanning tree.

There is no upper bound so we only need $I_N$ and it will contain all the other links with flow equal to 0.

Once we select a spanning tree, we can make an incidence matrix of just the spanning tree. In this case, we'll get:

Notice that the system above is not linearly independent. So, we can remove the last row and we get:

❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗

From slide 17 to end of pdf.