01.1 - Network flows - MM

Flow is defined as the number of events divided by a set amount of time.

It can be materials (goods), passengers (travelers) or vehicles (carriers) per unit of time.

assumption - large horizon of time

We work under the assumption that the Horizon of time is much grater than the largest O-D trip time.

Open and closed flows

open flows

Open flows are the ones where units originate at a source (ORIGIN) and disappear at a sink (DESTINATION).

Units on open flows follow a path:
A path is a chain of links, starting at node $p$ and ending at a different node $q$ .

A path can contain, in turn, cycles (which is not desirable). For these reason, only pure paths (without cycles) will be considered

It's given the graph below as an example

It shows 6 nodes and 10 links.

Let $x_{i}$ be the total amount of units that go through link $i$ . We can write some balance equations at every node:

{\begin{cases} Nodo 1: x_{1} - x_{8} = 10 \\ Nodo 2: - x_{1} + x_{2} + x_{4} + x_{5} + x_{7} = - 12 \\ Nodo 3: - x_{2} + x_{3} = 0 \\ Nodo 4: - x_{3} - x_{4} - x_{5} + x_{9} - x_{10} = - 13 \\ Nodo 5: - x_{5} + x_{6} = 0 \\ Nodo 6: - x_{7} + x_{8} - x_{9} + x_{10} = 15 \end{cases}

which is a linear system that can be written in matrix form:

[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ - 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & - 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & - 1 & - 1 & 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 0 & - 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 1 & - 1 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \\ x_{7} \\ x_{8} \\ x_{9} \\ x_{10} \end{matrix}] = [\begin{matrix} 10 \\ - 12 \\ 0 \\ - 13 \\ 0 \\ 15 \end{matrix}]

which is in the form:

A x = b

where:

We usually work under the assumption that

x_{i} \geq 0 \forall i

Sometimes, we can have 2 or more goods traveling on the same network. In this case, we have to write separate flow equations for each good.

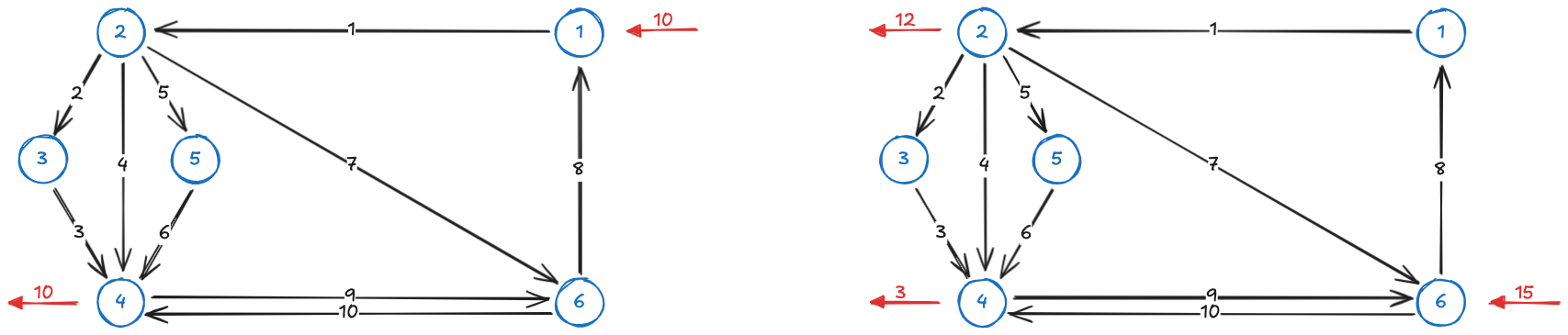
We have 2 linear systems:

For the graph on the left:

[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ - 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & - 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & - 1 & - 1 & 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 0 & - 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 1 & - 1 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \\ x_{7} \\ x_{8} \\ x_{9} \\ x_{10} \end{matrix}] = [\begin{matrix} 10 \\ 0 \\ 0 \\ - 10 \\ 0 \\ 0 \end{matrix}]

For the graph on the right

[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ - 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & - 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & - 1 & - 1 & 0 & 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 0 & - 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 1 & - 1 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \\ x_{7} \\ x_{8} \\ x_{9} \\ x_{10} \end{matrix}] = [\begin{matrix} 0 \\ - 12 \\ 0 \\ - 3 \\ 0 \\ 15 \end{matrix}]

The total flow is given by:

x = x^{1} + x^{2}

Considering one network and one flow compared to the same one network but 2 separate flows is very different.

open flows

In Closed flows units move in cycles. They never enter or exit the network, they just move across it.

Cycles are chains of links, starting at node $p$ and ending at the same node $p$ .

The figure below shows a network for a closed cycle:

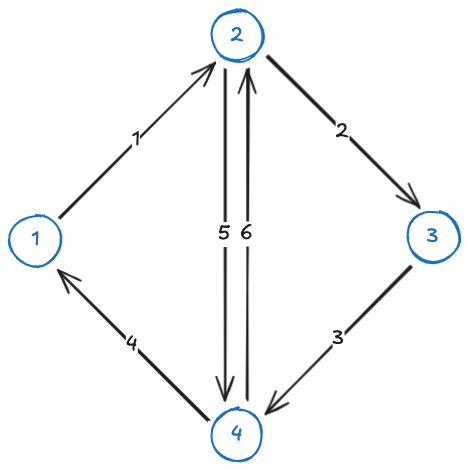
The network is defined by the following matrix:

[\begin{matrix} 1 & 0 & 0 & - 1 & 0 & 0 \\ - 1 & 1 & 0 & 0 & 1 & - 1 \\ 0 & - 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 1 & - 1 & 1 \end{matrix}]

From this network, 3 cycles are possible:

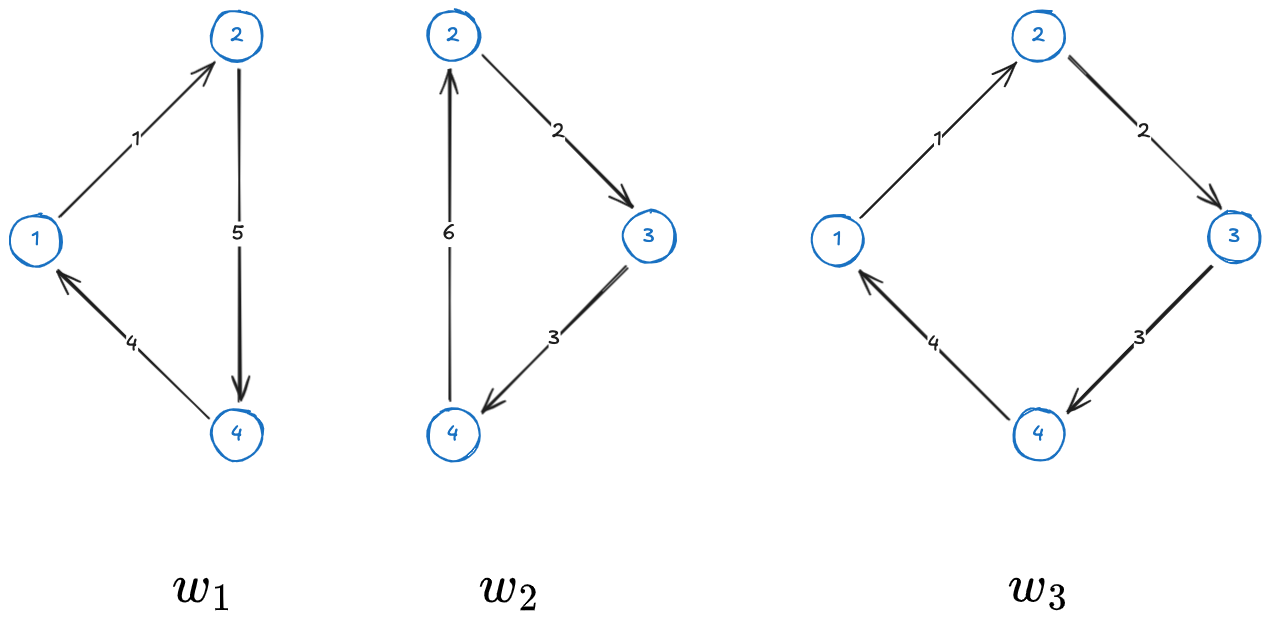
Each cycle can be identified by a vector, as follows:

w_{1} = [\begin{matrix} 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{matrix}], w_{2} = [\begin{matrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{matrix}], w_{3} = [\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \end{matrix}]

with $w_{i} \geq 0$ .

Each of these vectors contains a 1 in the position corresponding to a link that exists, and a 0 if the corresponding link is not part of the cycle.

Since there is never an input or output of units, the product between $B$ and any cycle $w_{i}$ always gives 0:

B w_{1} = 0, B w_{2} = 0, B w_{3} = 0

❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗

iPad