00 - Graph - MM
00 - Graph - MM
Graphs are useful mathematical models for representing urban and transportation networks.
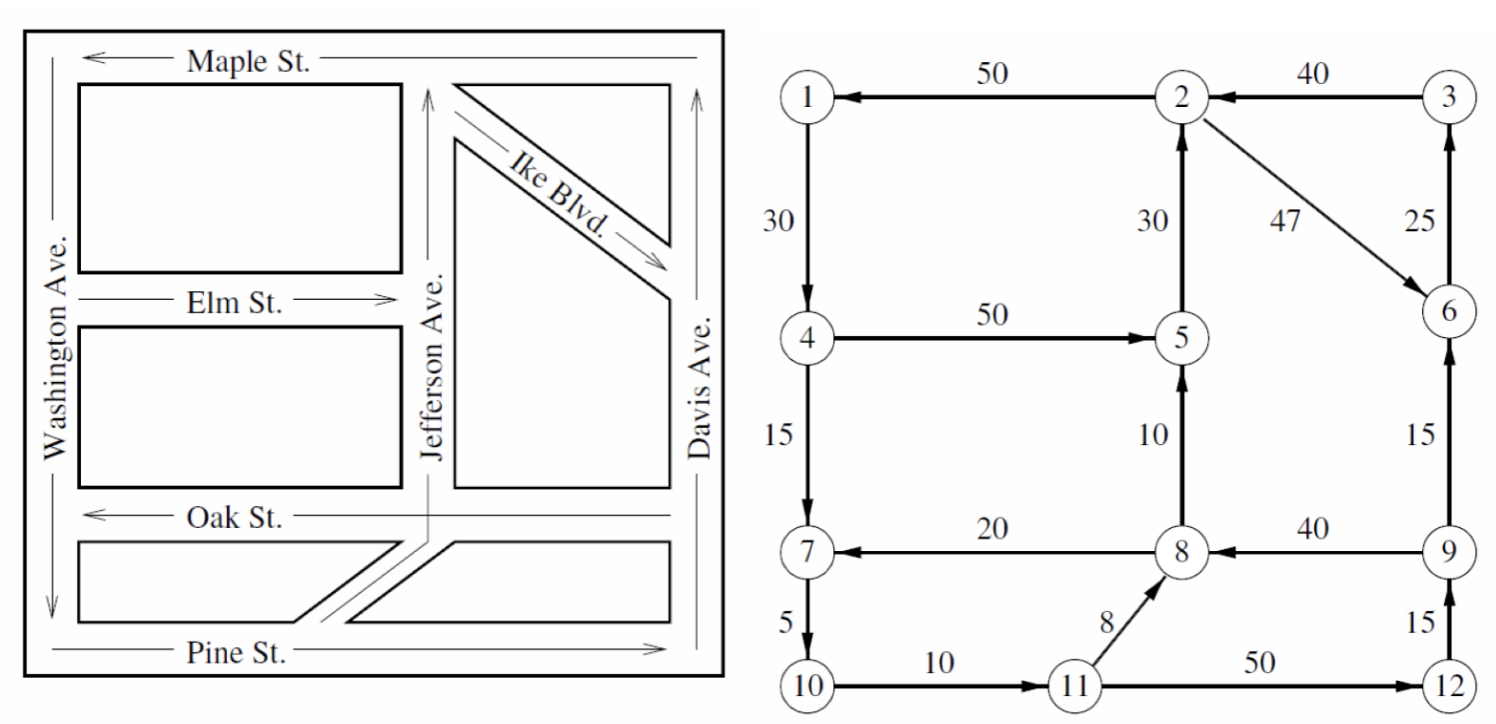
Directed graph
A directed graph is a set of
It is represented as
- Nodes are usually numbered with integers.
- Arcs are either named with integers, or with the pair of nodes they connect
For the example graoh above we would have:
Graph representation
Incidence matrix
07. Schematizzazione dell'offerta di trasporto#Matrice di incidenza
A graph is a just a diagram. We need to make calculations. We have to define a way to translate the graph into a mathematical instrument we can use.
Each graph can be written as a matrix, called incidence matrix.
- Each row represents a node
- Each column represents an arc or link
We can represent a graph through a matrix in which every row represents a node, and each column represents a link (links are also numbered).
The graph above gives the following incidence matrix:
Elements in a graph
Adjacency and Incidency
Forward star or Adjacency
A forward star, or Adjacency of a node
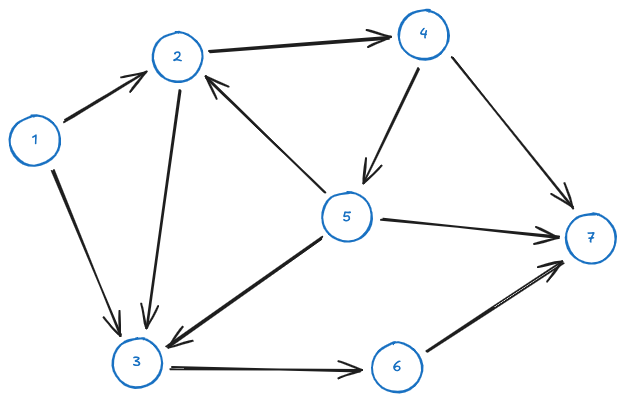
For example, given the graph below:

the forward star of node
By gathering the adjacency of all nodes, the number of links in A can be obtained:
Incidency
The incidency of node
Out-degree and In-degree
The out-degree of node
Path
A path is a chain of links, starting at node
Directed path
A directed path on a graph is a sequence of arcs
so that
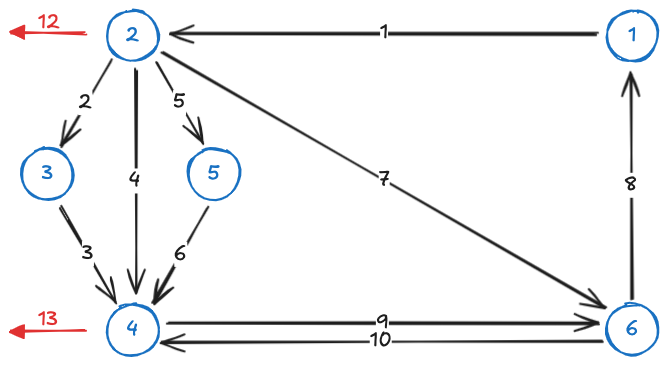
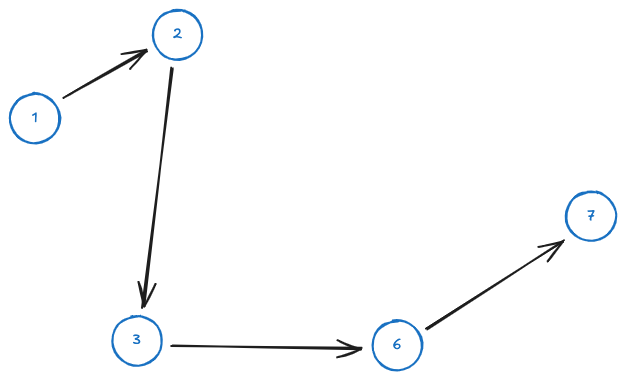
Given the following graph

a possible directed path si:
Undirected path
An undirected path on a graph is a sequence of arcs
so that
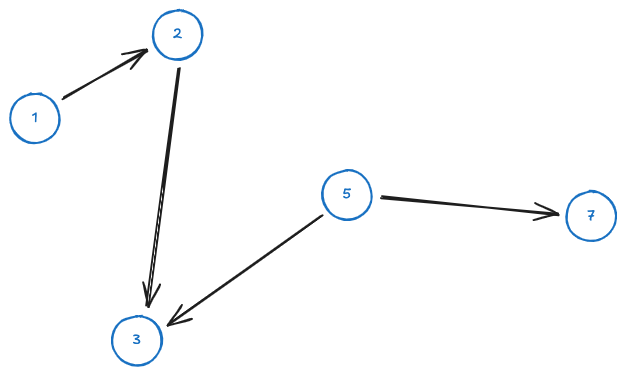
Given the graph

An undirected path can be:
Cycle
A cycle or directed cycle is a [[#Directed path]] with the additional condition
From the graph

a cycle is
There can also be undirected cycles, where the direction of links doesn't matter.
Connected nodes
Node-
Tree
A tree is a special type of graph that contains no cycles.
It can be directed or undirected.
Trees have the following characteristic:
A [[#Path]] is always a tree. More specifically, a [[#Directed path]] is always a directed tree.
BUT
A tree is not necesseraly a [[#Path]]
!700
%%🖋 Edit in Excalidraw%%
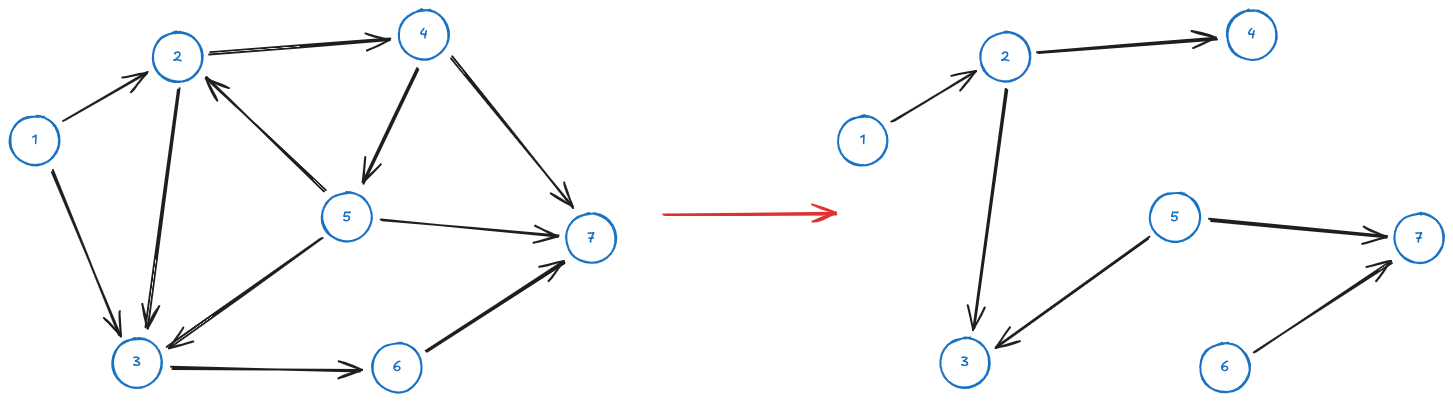
Spanning tree
A spanning tree is a part of graph
Rooted spanning tree
There exist a node, called the root node, which is connected with any other node in the network.
Also, the undirected path from a root node to any other node in the tree is unique (it's a #Spanning tree).
Storing and retrieving paths
In a directed #Spanning tree, we can store paths in a simple matrix.
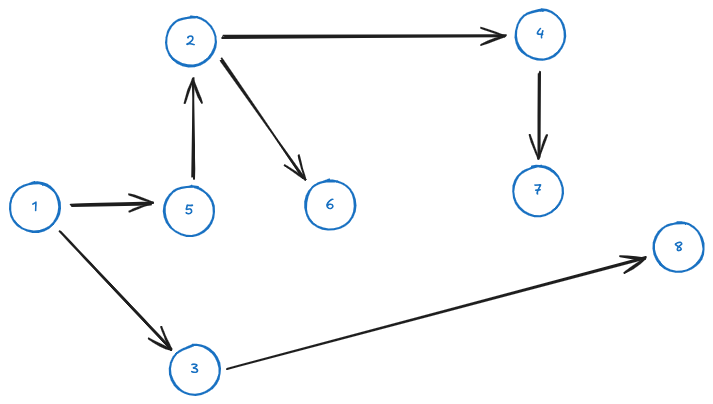
This tree can be stored as an array