Lab 1 - Introduction to AMPL
Lab 1 - Introduction to AMPL
AMPL IDE is an environment to run the AMPL system
AMPL is a language to run mathematical optimization programs.
It solves them by means of solvers. They are the ones that do the work. AMPL just manages them giving them a language.
- They are oriented to the development of models commonly used in OR
- The formulations are: understandable to other users and can be easily modified and extended.
- For solving the models, general purpose SOLVERS are used
- Usually there are environments suited for developement/debugging.
- AMPL language is very well suited and featured for complex data structures in large/specialized models
- Other languages: GAMS, CAMPS, L INGO.
AMPL is thought to shorten the time of developing mathematical problems.
Knapsack problem
In the knapsack problem, you need to pack a set of items, with given values and sizes (such as weights or volumes), into a container with a maximum capacity . If the total size of the items exceeds the capacity, you can't pack them all.
Let
# of pieces of type unit value of piece of type volume of the knapsack volume of unit of piece max number of units of type available

We want to maximaze the value we steal.
There are constrains (s.a):
The more valuable pieces are the ones with higher ratio:
I can fill the pack of volume
If I define what
with constrains
The problem can also be written in matrix form:
with constrains
The .mod file
The mod file defines the structure of the problem. It defines what everything is: like P is a set, a is a parameter... It doesn't assign values.

- .mod files - contain description. Everything we write
I define the parameters:
set P;
param a {j in P};
param b;
param c {j in P};
param u {j in P};
# I define a variable x
var X {j in P}
# I define the objective function
maxiaze beneficio: sum {j in P} c[j] * X[j]
# I define the constrains
subject to tiempo: sum {j in P} a[j] * X[j]<=b;
subject to Limites {j in P}: 0 <= X[j] <= u[j];
Capital letters matter. Names are case sensitive.
The .dat file
.dat files - contain the data that has to be compatible with the .mod file
It has to be consistent with what is in the .mod file.
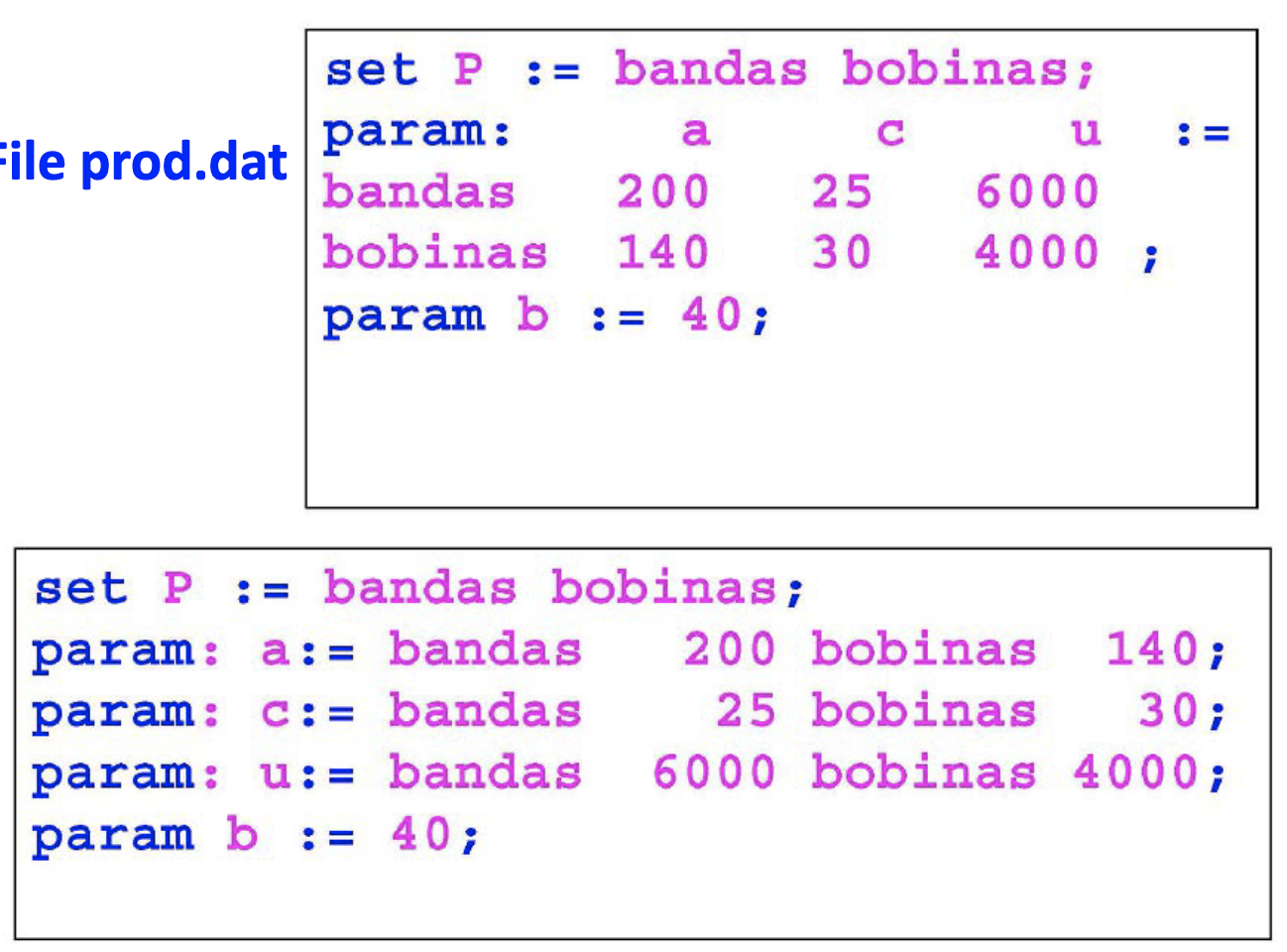
the aboves are two possible formats.
we define the set P with indexes "bandas" and "bobinas".
Then we assign values to the parameters.
a ha value 200 for "bandas" and 140 for "bobinas".
Execute
MsDoJ
open AMPL
AMPLE > get mod with command - ampl: model <fileName>.mod
AMPLE > get data with dat command - ampl: data <fileName>.dat
AMPLE > solve
We can work in 2 ways:
- IDE system - Amplide
- Terminal
- sw.exe to create a command window
There are 4 solvers in our systems:
- gurobi - Integer and linear programming
- cplex - Integer and linear programming
- minos - Non linear programming
- ??? - Non linear programming
Understanding a model we don't know
If we're given a model of which we don't know the content, there are some commands that can help:
show- shows the parametersdisplay <what To display>- shows value of variablesexpand- Tells me what is loaded in memory
minCost example
minCost.mod
Translates a graph.
- N: Ciudades (cities)
- A: Arcos (arcs)
This is said as: set ARCOS within (CIUDADES cross CIUDADES);
- This "within" tells that the arcs are included in the set of all possible arcs between all possible cities.
For network flow problems we don't use var and subject to for the flow variables and constrains.
We use 2 new commands:
arc(equivalent tovar)node(equivalent tosubject to)
is written as: node Nodo {k in CIUDADES}: net_in = domanda[k]-oferta[k]
The part in the write tells that
❗❗❗❗❗❗❗❗❗❗❗❗
❗❗❗ COMPLETARE ❗❗❗
❗❗❗❗❗❗❗❗❗❗❗❗