Assgm 2 - Traffic Assignment problem - MM

My parameters: [[Assgm 2 - Parameters - MM.pdf]]

Name	ID	File_XX.jpg	$c_{i j}$	$d_{i j}$	O-D Flow	Aug. factor for $c_{i j}$ at red links
Matteo Meloni	ca41844hp	18	2	0,1863	30	2.9430

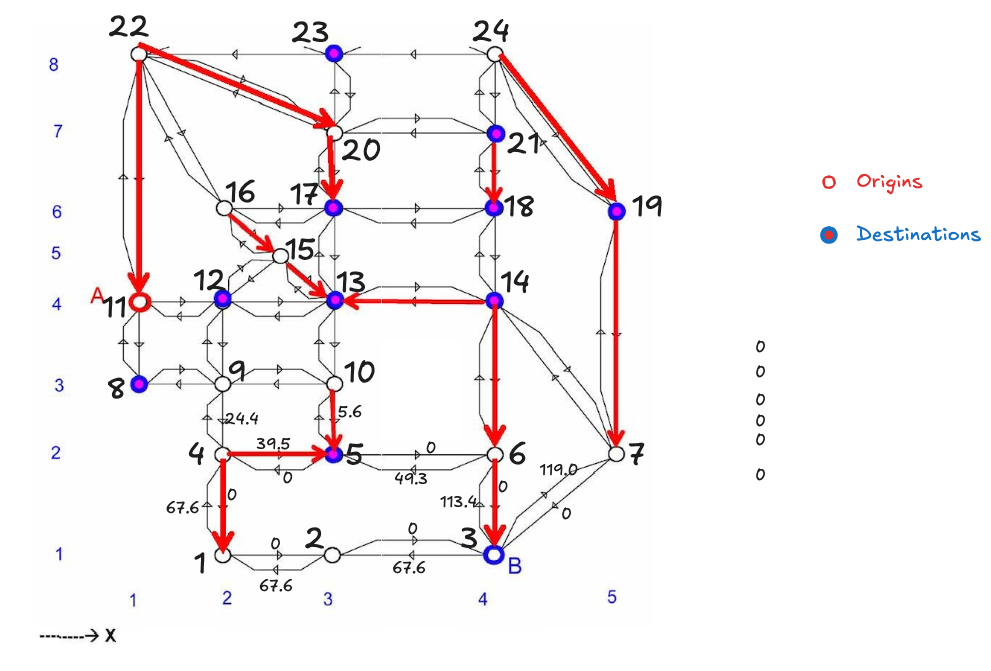
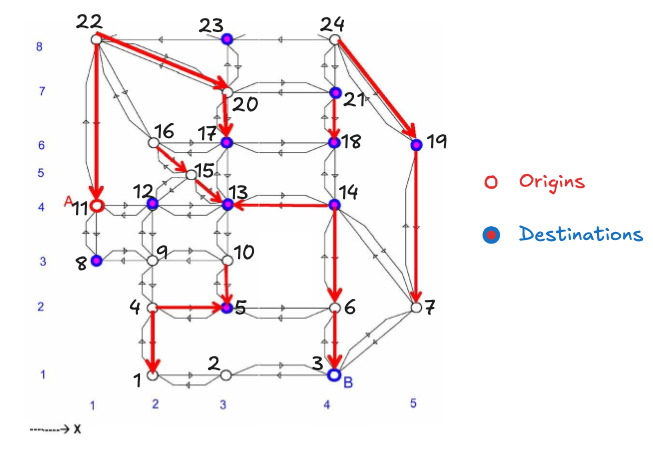
You are assigned the following network

The Volume delay function is the same for each link, and it's equal to:

s_{i j} (x) = c_{i j} + d_{i j} x_{i j}^{2}

where:

According to the assigned parameters, the values are as follows:

❗❗ Keep in mind, parameters have different names in the AMPL code...

What we have to do

Solve the whole problem (Beckmann's problem) minimizing the objective function in the MinCM2.mod file
Solve implementing the Frank-Wolfe Method in the .run file and using solvers only to solve the subproblem

Given the volume delay function:

t 0_{i j} (v_{i j}) = c_{i j} + {c a p}_{i j} v_{i j}^{2}

the Beckmann's problem is

min_{x_{i j}} \sum_{i j \in A} \int_{0}^{x_{i j}} t 0_{i j} (x) d x

Subject to

A v = b

where $A$ is the set containing all the links in the network

The objective function can be written explicitly:

\begin{aligned} \int_{0}^{v_{i j}} t 0_{i j} (x) d x & = \int_{0}^{v_{i j}} (c_{i j} + {c a p}_{i j} x_{i j}^{2}) d x \\ = c_{i j} v_{i j} + \frac{1}{3} {c a p}_{i j} v_{i j}^{3} \end{aligned}

In AMPL, the Beckmann's problem is problem $Q$ :

problem Q: v_k, v, N, flux_total, Vnl; # Traffic Assignment (Equilibrium problem) Definition

Which uses:

The objective function in the .mod file appears as

minimize Vnl: sum { (i,j) in links} (gamma * c[i,j] + cap[i,j] * (1/3) * v[i,j]^3);

which corresponds to

min_{v} V n l = min_{v} (γ c_{i j} + {c a p}_{i j} \frac{1}{3} v_{i j}^{3})

where:

Pick 4 OD pairs.
For each OD pair, pick 3 paths.

Picked OD pairs and paths:

(11, 17)
- (11, 12) (12, 15) (15, 16) (16, 17)
- (11, 12) (12,13) (13, 17)
- (11, 12) (12, 15) (15, 13) (13, 17)
(11, 14)
(3,)