Assgm 0 - Introductory Excercise - MM

Name (Name surname): Matteo Meloni ID: CA41844HP

Assgm 0

For the following multi-commodity network:

1--> 2 is required to transport g1 =400 flow units of commodity 1
3 --> 4 is required to transport g2= 400 flow units of commodity 2

$t_{0}$ = transportation cost per unit

Problem a

Using the corresponding AMPL model solve the problem (it is necessary first to edit the parameters file)

Problem a.1

a.1 - No joint capacity limits at links.

This is a multi-commodity problem.

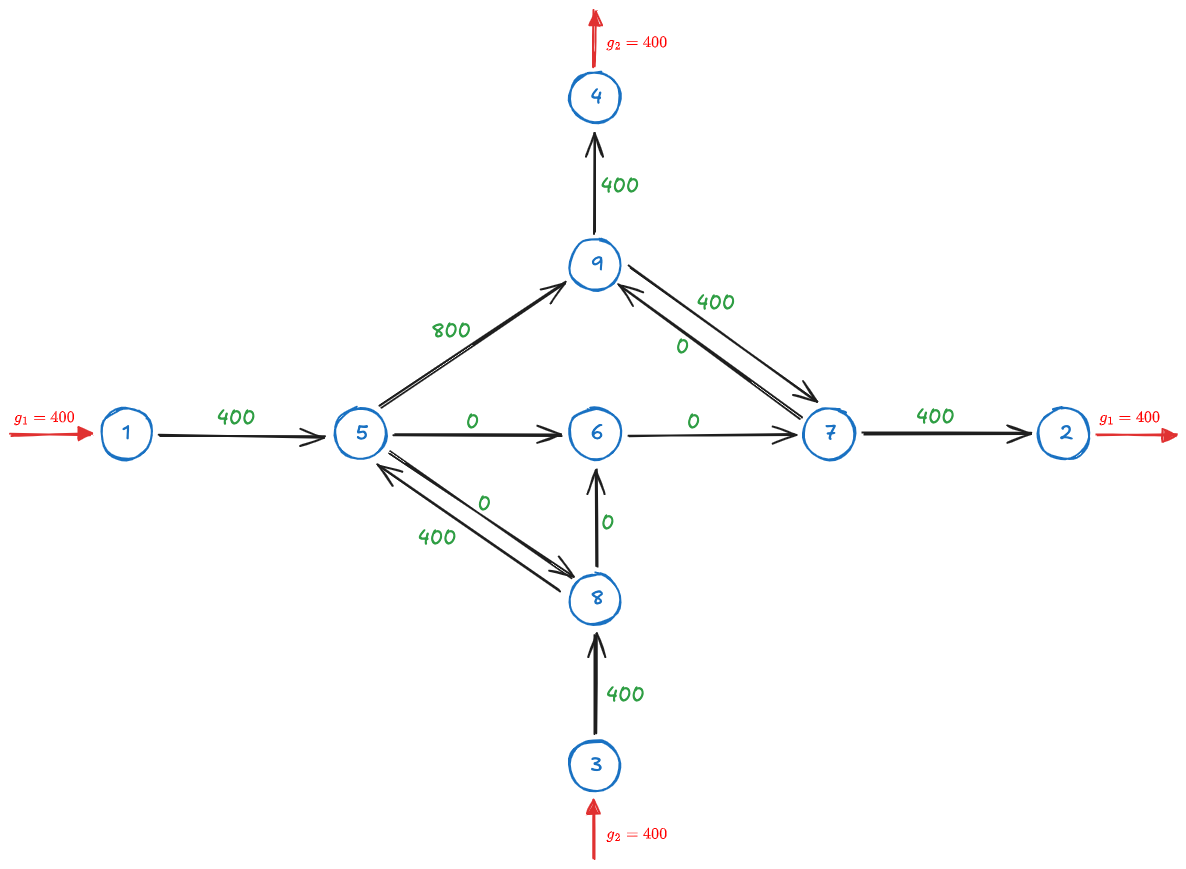
We use the MinCM2.mod model file in AMPL to solve it. The figure below shows the solution:

The solution has a total cost of 1232.

Problem a.2

Modify the AMPL model so that joint capacity constraints enter into play. Define the value of these joint capacities so that the solution found in #Problem a.1 is no longer feasible at one or more links.

The following constraints were added:

u_{59} = 300 u_{56} = 600

The new solution has a total cost of 1292 and is represented in the following figure:

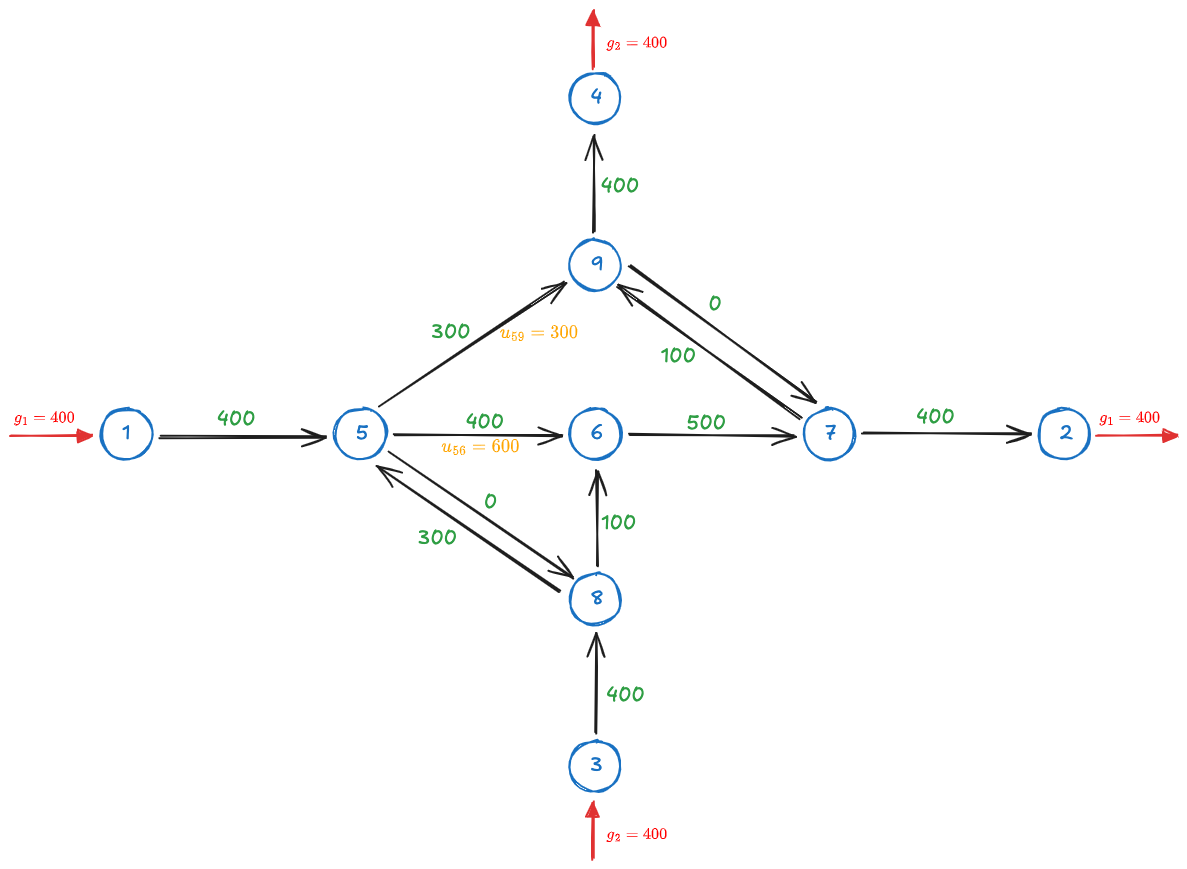
Notice how the constraint $u_{56}$ doesn't affect the solution, given that the upper bound is greater than the optimal amount of units through that same link.

We can see that the new upper bounds limited the amount of goods that could go through link 5-9. Therefore, some good units are rerouted along other links.

Problem b

Assume now that there is only a single commodity in the network and that it is necessary to transport 400 & 400 from 1,3 to 2,4 (no capacity limits). Solve the problem using AMPL and compare the solutions with those obtained in a.1). (Hint: adapt and use Mincost.mod, Mincost.dat)

For this problem, the MinCost.mod model was used.

The solution in this case is given by the graph below. The total cost is now equal to 1152.

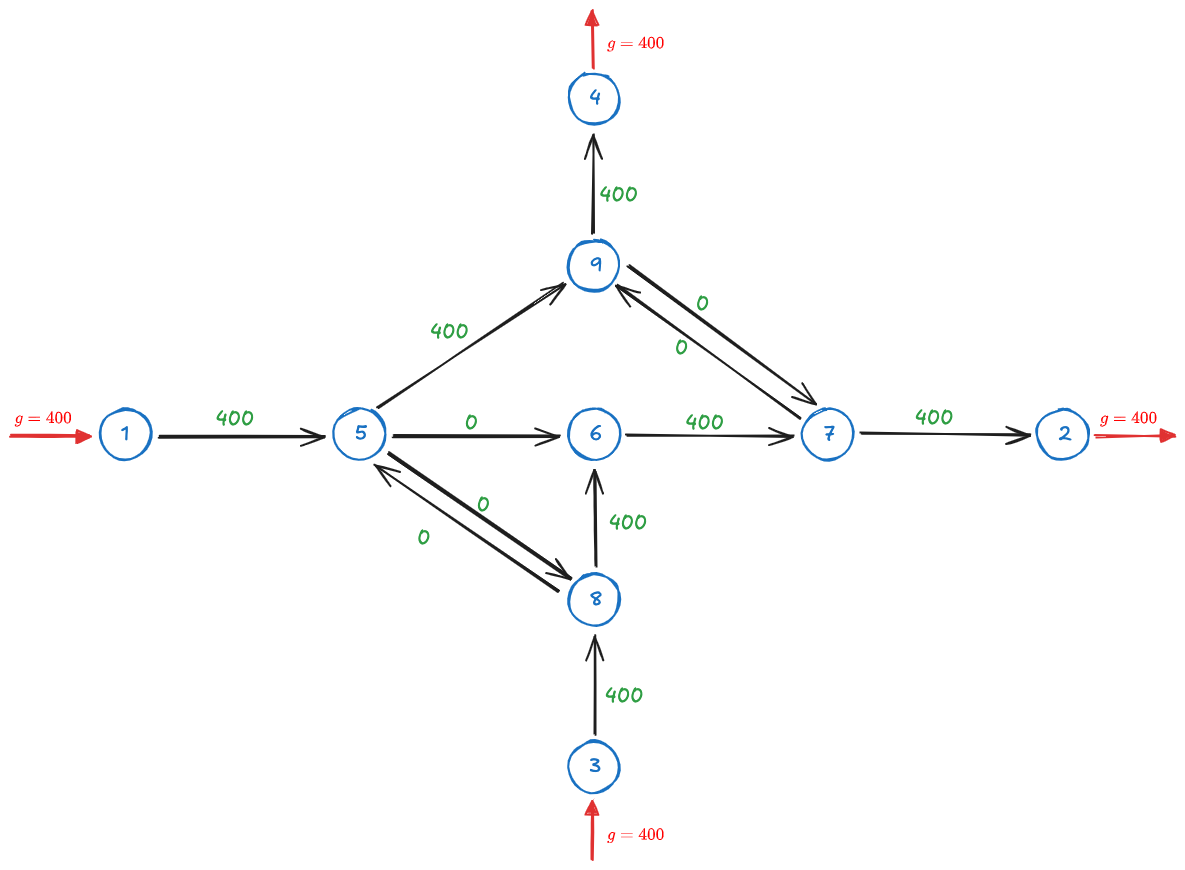
In this case the total cost is lower than the one in #Problem a. This is expected. In the single commodity problem, we don't put constraints on where the units go as a function of where they are from. For example, in a), units from node 1 had to exit at node 2. Now this is not necessary, and in fact, the optimal solution has them exiting at node 4.